2. Базисные показатели характеризуют итоговый результат всех изменений в уровнях ряда от периода базисного уровня до данного (i-го) периода.

3. Цепные показатели характеризуют интенсивность изменения уровня от одного периода к другому в пределах того промежутка времени, который исследуется.

4. Абсолютный прирост выражает абсолютную скорость изменения ряда динамики и определяется как разность между данным уровнем и уровнем, принятым за базу сравнения.

5. Абсолютный прирост (базисный)

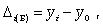6.  (9.1)

7. где y_i - уровень сравниваемого периода; y₀ - уровень базисного периода.

8. Абсолютный прирост с переменной базой (цепной), который называют скоростью роста,

9.  (9.2)

10. где y_i - уровень сравниваемого периода; y_i-1 - уровень предшествующего периода.

11. Коэффициент роста K_i определяется как отношение данного уровня к предыдущему или базисному, показывает относительную скорость изменения ряда. Если коэффициент роста выражается в процентах, то его называют темпом роста.

12. Коэффициент роста базисный

13.  (9.3)

14. Коэффициент роста цепной

15.  (9.4)

16. Темп роста

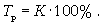17.  (9.5)

18. Темп прироста Т_П определяется как отношение абсолютного прироста данного уровня к предыдущему или базисному.

19. Темп прироста базисный

20.  (9.6)

21. Темп прироста цепной

22.  (9.7)

23. Темп прироста можно рассчитать и иным путем: как разность между темпом роста и 100 % или как разность между коэффициентом роста и 1 (единицей):

24. 1) Т_п = Т_р - 100%; 2) Т_п = K_i - 1. (9.8)

25. Абсолютное значение одного процента прироста A_i . Этот показатель служит косвенной мерой базисного уровня. Представляет собой одну сотую часть базисного уровня, но одновременно представляет собой и отношение абсолютного прироста к соответствующему темпу роста.

26. Данный показатель рассчитывают по формуле

27.  (9.9)

28. Для характеристики динамики изучаемого явления за продолжительный период рассчитывают группу средних показателей динамики. Можно выделить две категории показателей в этой группе: а) средние уровни ряда; б) средние показатели изменения уровней ряда.

29. Средние уровни ряда рассчитываются в зависимости от вида временного ряда.

30. Для интервального ряда динамики абсолютных показателей средний уровень ряда рассчитывается по формуле простой средней арифметической:

31.  (9.10)

32. где n - число уровней ряда.

33. Для  моментного динамического ряда средний уровень определяется следующим образом.

34. Средний уровень моментного ряда с равными интервалами рассчитывается по формуле средней хронологической:

35.  (9.11)

36. где n - число дат.

37. Средний уровень моментного ряда с неравными интервалами рассчитывается по формуле средней арифметической взвешенной, где в качестве весов берется продолжительность промежутков времени между временными моментами изменений в уровнях динамического ряда:

38.  (9.12)

39. где t - продолжительность периода (дни, месяцы), в течение которого уровень не изменялся.

40. Средний абсолютный прирост (средняя скорость роста) определяется как средняя арифметическая из показателей скорости роста за отдельные периоды времени:

41.    (9.13)

42. где y_n - конечный уровень ряда; y₁ - начальный уровень ряда.

43. Средний коэффициент роста ( ) рассчитывается по формуле средней геометрической из показателей коэффициентов роста за отдельные периоды:

44.  (9.14)

45. где К_р1 , К_р2 , ..., К_{р n-1} - коэффициенты роста по сравнению с предыдущим периодом; n - число уровней ряда.

46. Средний коэффициент роста можно определить иначе:

47.  (9.15)

48. Средний темп роста, %. Это средний коэффициент роста, который выражается в процентах:

49.  (9.16)

50. Средний темп прироста  , %. Для расчета данного показателя первоначально определяется средний темп роста, который затем уменьшается на 100%. Его также можно определить, если уменьшить средний коэффициент роста на единицу:

51.  (9.17)

52. Среднее абсолютное значение 1% прироста можно рассчитать по формуле

53.  (9.18)

13. Статистические показатели динамики социально-экономических явлений

Для обобщающей характеристики динамики исследуемого явления за ряд периодов определяют различного рода средние показатели. Существуют две категории этих показателей:

1) средние уровни ряда;

2) средние показатели динамики данного ряда.

Метод расчета среднего уровня динамического ряда зависит от вида временного ряда.

В интервальных рядах динамики из абсолютных уровней средний уровень определяется по формуле средней арифметической:

простой (при равных интервалах):

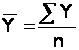, (7)

где   - сумма абсолютных уровней ряда;

n - число уровней.

взвешенной (при неравных интервалах):

, (8)

где Y - уровни ряда динамики, сохраняющиеся без изменения в течение промежутка времени t;

t - длительность интервалов времени (дней, месяцев) между смежными датами.

Для моментного ряда средний уровень определяется с помощью средней хронологической:

простой (для ряда динамики с равностоящими уровнями)

, (9)

где Y - уровни периода, за который делается расчет;

m - число уровней.

взвешенной (для ряда динамики с неравностоящими уровнями):

, (10)

где Yi, Yn - уровни ряда динамики;

t - интервал времени между уровнями.

При определении средних уровней временного ряда нужно иметь в виду, что средняя будет достаточно надежной характеристикой ряда динамики, если она характеризует период с более или менее стабильными условиями развития. Если же за исследуемый период можно выделить этапы, в течение которых условия развития существенно менялись, то пользоваться общей средней не всегда целесообразно, а предпочтение нужно отдать средним, рассчитанным по отдельным периодам.

Средний абсолютный прирост представляет собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики. При базисном способе расчета, чтобы определить средний абсолютный прирост, для этого определяется разность между конечным Уn и базисным У0 уровнями изучаемого периода, которая делится на m-1 субпериодов:

, (11)

где m - число уровней ряда динамики в изучаемом периоде, включая базисный. При цепном способе расчета для определения среднего абсолютного прироста сумма цепных абсолютных приростов делится на их число:

, (12)

где n - число цепных абсолютных приростов в изучаемом периоде.

Средний темп (коэффициент) роста является обобщающей характеристикой индивидуальных темпов (коэффициентов) роста ряда динамики. Для базисного способа расчета средний темп (коэффициент) роста будет определяться по формуле:

, (13)

. (14)

Для определения среднего темпа (коэффициента) роста цепным способом применяется формула средней геометрической:

100, (15)

, (16)

где Кр1, Кр2,..., Крn - индивидуальные (цепные) коэффициенты роста;

n - число индивидуальных темпов роста

Средний темп (коэффициент) прироста рассчитывается на основе средних темпов (коэффициентов) роста по следующим формулам:

, (17),  . (18)

Среднее значение одного процента прироста определяется только для цепного способа расчета по формуле:

. (19)

Данные показатели динамики находят практическое применение во всех расчетах, где требуется изучение изменения социально-экономических явлений во времени.