1.8. Расчёт схемы методом наложения (суперпозиции) токов

Этот метод использует свойства линейных цепей алгебраически сумми­ровать токи от многих источников энергии в конкретной ветви. Его удобно применять, если требуется определить ток в какой-либо одной ветви. Порядок расчёта цепи с применением этого метода сводится к следующему. Рассчитыва­ется величина тока (с учётом его направления) в выбранной ветви в предполо­жении, что в цепи действует только один источник энергии. При этом «лиш­ние» генераторы э.д.с. заменяются перемычками или их внутренними сопро-

тивлениями, а ветви с «лишними» генераторами тока разрываются или вместо генераторов тока ставятся резисторы, сопротивления которых соответствуют значениям внутренних сопротивлений неидеальных генераторов тока. Расчёт повторяется для всех источников энергии в цепи. Затем полученные значения токов в выбранной цепи суммируются алгебраически, то есть с учётом их на­правлений. Полученное значение тока является искомым.

Выполним расчёт тока резистора R3 в схеме рисунка 1.8 методом нало­жения. Оставим в схеме источник E1, заменив источник E2 перемычкой. При этом приходим к схеме, предложенной на рисунке 1.12.

II

13

a

R1 100Ом

R2 300Ом

E1 10В

12

ь

R3 96Ом

Рисунок 1.12 Представляет интерес ток 13 , порядок расчёта которого может быть сле­дующим.

Рассчитаем сопротивление параллельно включенных резисторов R2 и R3:

„, R1 ■ R3

R = .

R2 + R3

Рассчитаем ток через резистор R1:

I1

El

R+R1

Определим падение напряжения между точками a и b:

R' U _h = R-Il = El .

R'+Rl

Рассчитаем величину тока через резистор R3, определяемую величиной э.д.с. E1:

^U .

I3' = ^ab R3

Направление тока показано на рисунке 1.12.

Рассмотрим поведение схемы в том случае, когда действует э.д.с. E2. При

этом вместо источника E1 поставим перемычку, как показано на рисунке 1.13.

II

13

a

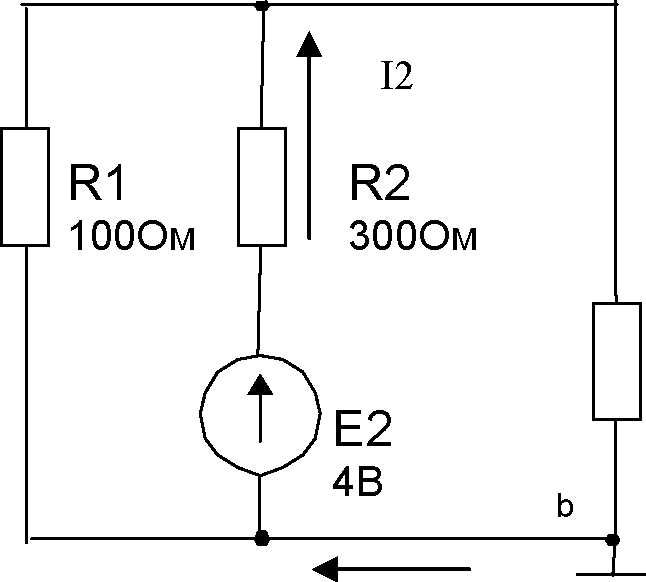
R3 96Ом

Рисунок 1.13 Для полученной схемы осуществим расчёт тока I3’’, который течёт через рези­стор R3 под действием э.д.с. E2. В отличие от схемы рисунка 1.12, в данной схеме параллельно оказываются включены резисторы R1 и R3. Расчёт ведётся подобно выполненному расчёту для схемы рисунка 1.12.

В результате реальное значение тока через резистор R3 в исходной схеме рисунка 1.8, которое формируется под действием двух источников э.д.с.: E1 и E2, определится суммой:

I3 = I3'+I3' '. Задание: осуществите расчёт предложенной на рисунке 1.8 схемы методом наложения токов с учётом сопротивлений резисторов и проверьте результа­ты моделированием.

1.9. Метод эквивалентного генератора

Используется при определении тока или падения напряжения на одной ветви или на одном компоненте. При этом сколько угодно сложная схема при­водится к простейшей эквивалентной схеме, которая содержит идеальный ис­точник э.д.с. Е и внутренний резистор с сопротивлением R_в (смотри рисунок 1.1). Компоненты ветви, в которой следует определить величину тока, оказы­ваются для полученного источника внешней нагрузкой.

Для определения э.д.с. и внутреннего сопротивления R_в в исходной схеме рассматривают два режима: холостого хода и короткого замыкания. В режиме холостого хода резистор нагрузки или ветвь, в которой следует рассчитать ток, отключают и рассчитывают выходное напряжение цепи. Рассчитанное напря­жение приравнивают к величине э.д.с. Е. Режим короткого замыкания предпо­лагает, что сопротивление выделенной ветви равно нулю. При этом рассчиты­вают ток короткого замыкания 1_кз, который позволяет определить внутреннее сопротивление эквивалентного источника э.д.с. по формуле:

R_в=E/I_кз.

Рассмотрим пример расчёта схемы, предложенной на рисунке 1.8. Ста­вится задача рассчитать падение напряжения и ток в резисторе R3. Исходный вид схемы и схема после преобразования показаны на рисунке 1.14.

На холостом ходу предполагается отсутствие резистора R3, то есть цепь резистора R3 оказывается разорванной. При этом необходимо рассчитать паде­ние напряжения между точками а и Ь. Воспользуемся вторым законом Кирхго­фа для оставшейся цепи:

E\-E2 = U\ + С/2,

где С/1 = R1 ⋅ II, U2 = R2⋅Il.

Это позволяет рассчитать величину тока II:

_тл Е1-Е2 10-4 _л

IX = = = \5мА

RI + R2 100 + 300

II

a

R1 100Ом

Е1 ( t . юВ V ' JE2

4В

13

I2

R2 300Ом

b

R3 96Ом

^—

a O

R_в

75Ом

E 8,5В

b

o

13

R3 96Ом

а б

Рисунок 1.14 Искомое напряжение может быть определено двумя способами. В первом случае оно представляется с использованием ветви El, R1:

U _л =El-Rl-Il. Во втором случае напряжение между точками а и b определится с исполь­зованием ветви Е2, R2:

U _аЪ = E2 + R2-Il = 4 + 300-15-1СГ³ =8,5В.

Рассчитайте искомое напряжение с использованием ветви El, R1 и сравните результаты.

Таким образом, э.д.с. эквивалентного генератора будет равна:

E = U_ab =8,5В.

Рассчитаем ток короткого замыкания. В этом случае вместо резистора R3 следует поставить перемычку. Искомый ток будет равен сумме токов от источ­ника Е1 и от источника Е2:

Е\ Е2 10 4 „

/ = — + — = + = 0.1133А = 113,ЗмА

R\ R1 100 300

Ток короткого замыкания позволяет рассчитать внутреннее сопротивле­ние эквивалентного генератора э.д.с:

Е 8,5

R_В

I_кз 0.1133

75Ом .

Используя эквивалентную схему всей цепи, представленную на рисунке

1.14б, легко рассчитать ток резистора R3:

Е 8,5

13 = = = 0,0497А = 49,7мА

R_В + R3 75 + 96

Падение напряжения на резисторе R3 будет равно:

U _аЪ = U_R3 =R3-I3 = 96- 0,0497 = 4,77 В