2.2.2 Переходные процессы в простейших электрических цепях

Рассмотрим поведение интегрирующих и дифференцирующих цепей при воздействии на их входы импульсных сигналов.

Для интегрирующей цепи (рисунок 2.14а) составим дифференциальное уравнение, которое описывает её поведение при действии на вход сигнала щ (t) = щ . Выходной сигнал снимается с конденсатора, то есть справедливо ра­венство: и_с =и₂. По закону Кирхгофа можно записать:

щ =R-i_c +u_c. Для конденсатора справедливо:

С ■ du_c = г_с ■ dt.

Выразим ток из этого выражения и подставим в предыдущую формулу:

du_r

R-С ~ + и_с =щ .

dt

Решение этого уравнения состоит из суммы общего решения однородного уравнения и частного решения неоднородного уравнения при заданном вход­ном воздействии. Если на вход цепи действует ступенчатый сигнал с амплиту­дой £, то в установившемся режиме по окончании переходных процессов на выходе установится напряжение и_Су=Е. Это частное решение уравнения. Ре­шим однородное уравнение, которое получается из общего уравнения цепи от­брасыванием правой части:

„ du_r

R-С + и_с = 0 .

dt

Характеристическое уравнение для этого случая предложено ниже:

RCa+1=0.

Отсюда получим: а = .

RC

Решением однородного уравнения будет следующее уравнение:

-t/ u_Cп = U₀e ^/RC .

Общее решение выглядит как сумма:

и_с =E + U₀e~yR_r .

Определим значение неизвестной константы и₀, приняв равенство t = О .

В начальный момент времени напряжение на конденсаторе не может мгновенно измениться, учитывая закон коммутации для конденсаторов. То есть начальное напряжение на конденсаторе равно нулю. Тогда справедливо равенство:

Е + U₀ = О .

Отсюда получим равенство: -E = U₀. В окончательном виде выходное напря­жение интегрирующей цепи меняется при воздействии ступенчатого сигнала по экспоненте с постоянной времени t = RC:

и₂ =Е\^-е~У„_г).

Если интегрирующая цепь строится на основе индуктивности, то постоянная

времени в выражении для выходного сигнала будет равна г = —.

R

При воздействии импульса поведение интегрирующей цепи при условии со­блюдения неравенства t_и>5z, где t_и - длительность импульса входного сигнала, подобно предложенному на рисунке 2.19.

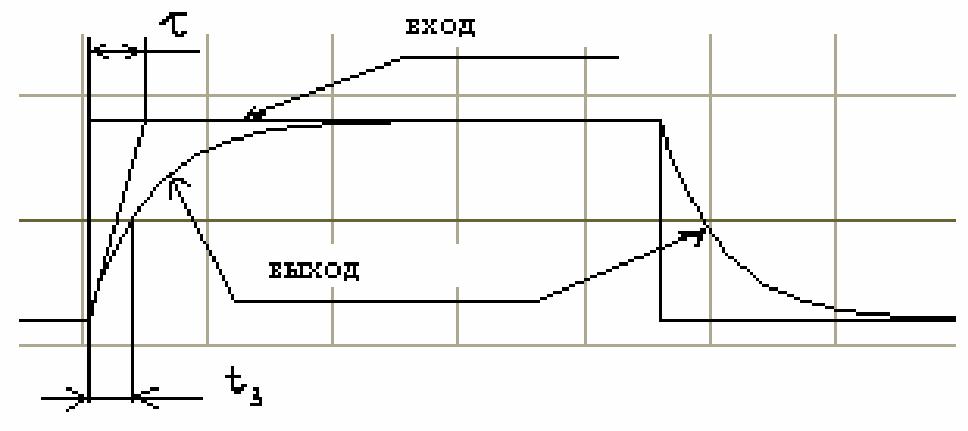
Рисунок 2.19

Интегрирующая цепь задерживает фронт входного импульса примерно на величину t_з *=0.7г, что показано на рисунке. Постоянную времени можно изме­рить с помощью осциллограммы так, как показано на рисунке. Из точки начала экспоненциального сигнала проводится касательная до точки пересечения с ус­тановившимся уровнем.

Для предложенных на рисунке 2.16 дифференцирующих цепей можно также определить реакцию на входной импульс. Выходное напряжение этих це­пей при действии ступеньки на входе опишется выражением:

^ -У_т и₂ = Е -е ^/т.

В момент окончания действия импульса реактивный элемент (например, конденсатор) будет отдавать энергию в выходную цепь, формируя при этом экспоненциальный импульс противоположной полярности, как показано на ри­сунке 2.20:

-у

и₂ = -Е-е ^/т.

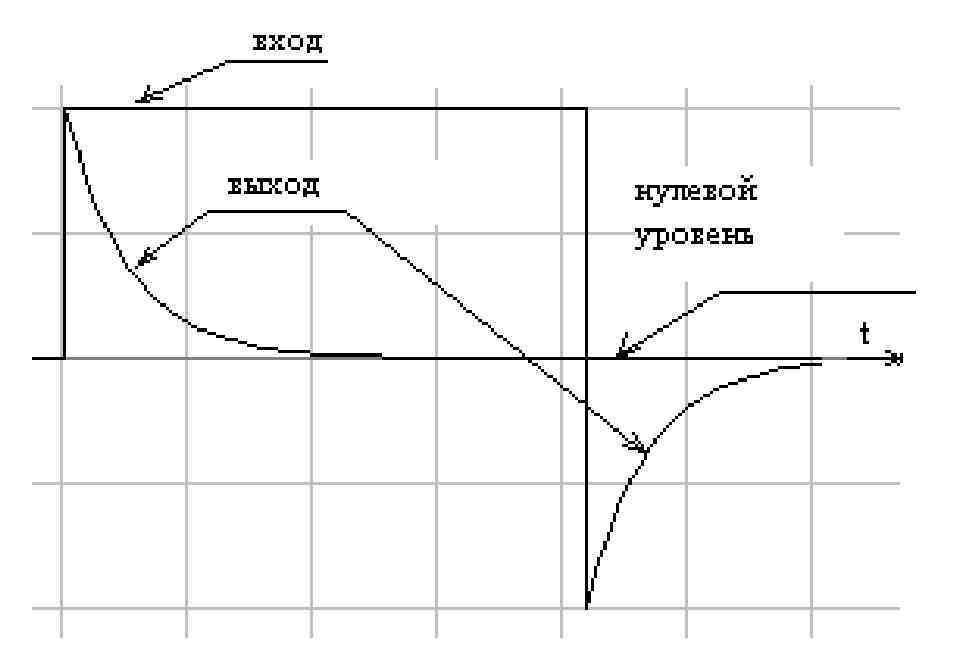
Рисунок 2.20 Дифференцирующая цепь формирует на выходе по нарастающему фрон­ту входного сигнала экспоненциальный кратковременный импульс положи­тельной полярности, а по спадающему фронту входного сигнала формирует им­пульс обратной полярности. Длительность импульса примерно равна t_и ≈ 0.7τ.

Если на вход дифференцирующей цепи подаётся импульс с выхода логи­ческого элемента, то есть с уровнями, соответствующими логическим, то с по­мощью логического элемента на выходе цепи можно сформировать кратковре­менный импульс упомянутой длительности, имеющий достаточно хорошие фронты.

Рассмотренные цепи часто используются именно для формирования им­пульсов с требуемыми временными параметрами.