2.1.6 Частотные свойства простейших электрических цепей

Обратим внимание на интегрирующие и дифференцирующие цепи, кото­рые находят широкое применение в электронике и в средствах вычислительной техники, на основе которых могут создаваться сложные цепи выделения и спектрального преобразования аналоговых сигналов.

На рисунке 2.15 предложены две схемы интегрирующих цепей, поведе­ние которых с частотой похоже. У каждой схемы имеется аналоговый вход и выход, что позволяет их рассматривать как примеры линейных пассивных че-

тырёхполюсников. Используя комплексный метод, определим зависимость вы­ходного сигнала от входного для схемы рисунка 2.15а.

а б

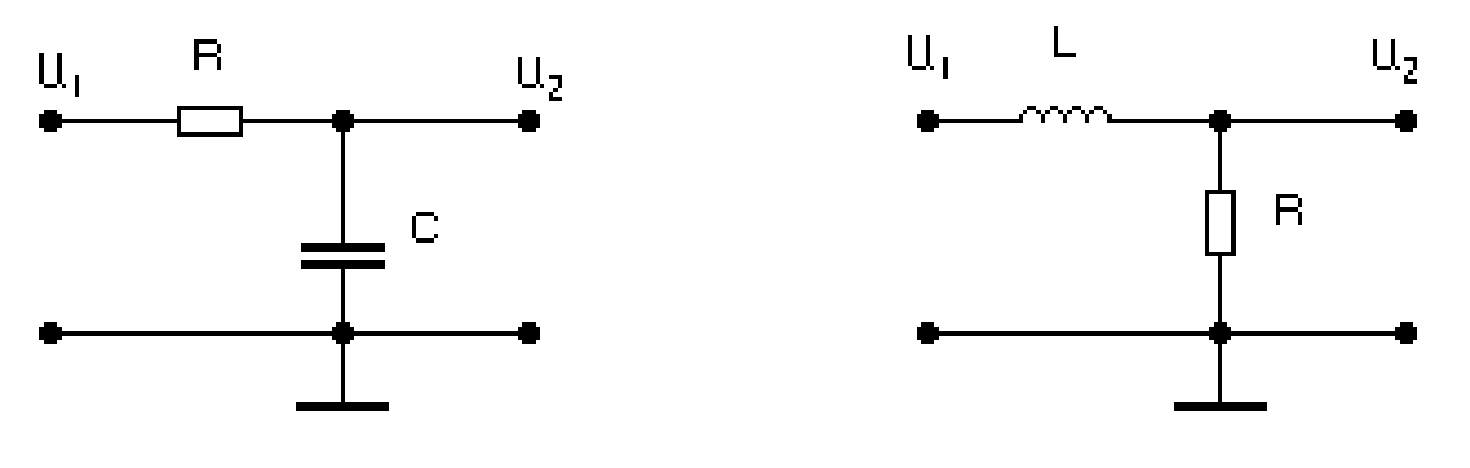
Рисунок 2.15

Комплексное изображение выходного сигнала U₂ в зависимости от

входного сигнала U₁ определится с учётом изображений для реактивного со­противления конденсатора x_C = ¹ и для сопротивления резистора R=R сле-jωC

дующим образом:

x_C

U₂=U_X

R+ x_C

Частотные свойства предлагаемой схемы определятся выражением:

H(ja)

1 jcoC 1

R _| 1 \ + jo)RC jcoC

Избавимся от комплексного числа в знаменателе умножением числителя и зна­менателя на комплексно-сопряжённое знаменателю число и преобразуя полу­ченное выражение:

. _ч 1 1- iaRC 1 1- icoRC

H(ja>) = = • ^J.

\ + jcoRC 1- jcoRC M + (coRC)² Jl + (coRC)²

Амплитудно-частотные свойства интегрирующей цепи характеризуются моду­лем полученного выражения:

• ч 1

\H(ja>)\

Амплитудно-частотная характеристика (АЧХ ) описывается этим выражением.

Фазо-частотные свойства цепи определятся зависимостью фазовой задержки выходного сигнала относительно входного, которую можно определить из по­лученного выражения следующим образом:

(р(а) = arctg(-coRC). При о=0 коэффициент передачи равен единице, то есть |#(0)| = 1, а ср = 0.

В полученных выражениях представляет интерес частота, на которой ко­эффициент передачи амплитуды уменьшается до величины —= « 0,707. Фазовая

V2

задержка при этом равна -45°. Соответствующая угловая частота ωгр считается верхней частотой пропускания или граничной частотой передачи сигнала. Оп­ределяется эта частота из равенства: со RC = 1. Из этого равенства определим

граничную частоту передачи (предложенная цепь не усиливает сигнал):

1 1

т, = или f = .

гр RC _гр ItzRC

С ростом частоты коэффициент передачи уменьшается. Если частота су­щественно выше граничной, то справедливо примерное равенство:

со

\H(jco)\ « —^гр . со

Коэффициент передачи может быть представлен в децибеллах следую­щим образом:

\H(jco)\ = 20-lg

со

гр

СО

дБ

Из этого выражения видно, что увеличение частоты сигнала в десять раз приводит к уменьшению коэффициента на 20дБ. На рисунке 2.16 предложены амплитудно-частотные характеристики интегрирующей цепи при линейном масштабе (2.16а) и при логарифмическом масштабе (2.16б) по оси амплитуды. Масштаб по частоте в обоих случаях логарифмический. АЧХ в логарифмиче­ском масштабе легко аппроксимируется двумя отрезками прямых линий. Эта особенность подобных характеристик широко используется для объяснения по-

ведения четырёхполюсников, осуществляющих спектральное преобразование сигналов.

Произведение RC определяет значение постоянной времени интегрирую­щей цепи τ: τ= RC .

а б

Рисунок 2.16 Предложенная на рисунке 2.15б схема анализируется подобным же обра­зом и ведёт себя аналогично. Но при этом следует учесть тот факт, что посто­янная времени этой цепи равна: г = —. АЧХ определится из выражения:

R

\H(ja>)\

Интегрирующие цепи можно рассматривать как простейшие фильтры низких частот, которые пропускают сигналы с частотами от нулевой до гра­ничной частоты.

Если компоненты предложенных на рисунке 2.15 схем поменять местами, то будем иметь дело с дифференцирующими цепями (рисунок 2.17).

а

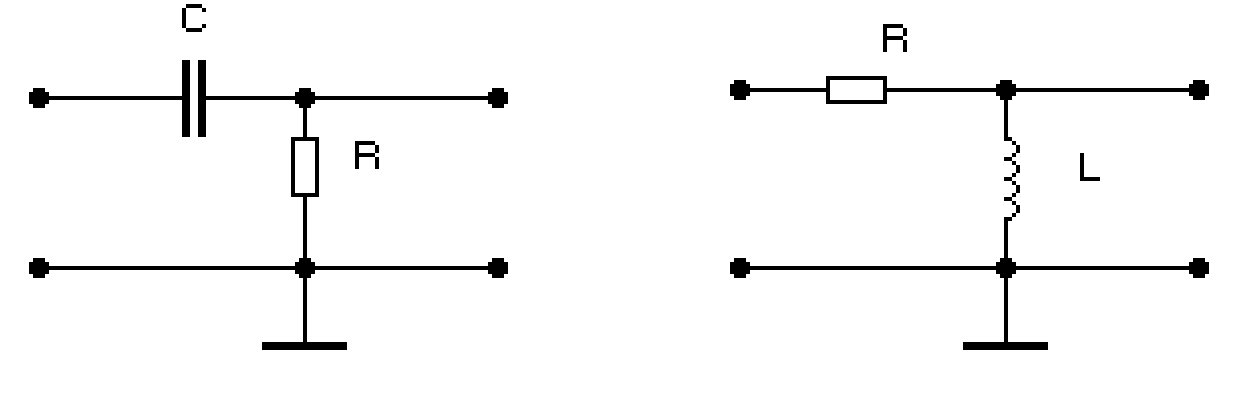
б

Рисунок 2.17 Эти цепи характеризуются теми же постоянными времени, но являются в отличии от интегрирующих цепей фильтрами высоких частот. То есть они про­пускают гармонические сигналы, частоты которых выше нижней граничной частоты передачи. Нижняя граничная частота передачи определяется из выра­жения: ф_гр=у Частотные свойства дифференцирующих цепей представлены

предложенными на рисунке 2.18 характеристиками с теми же масштабами по частоте и амплитуде.

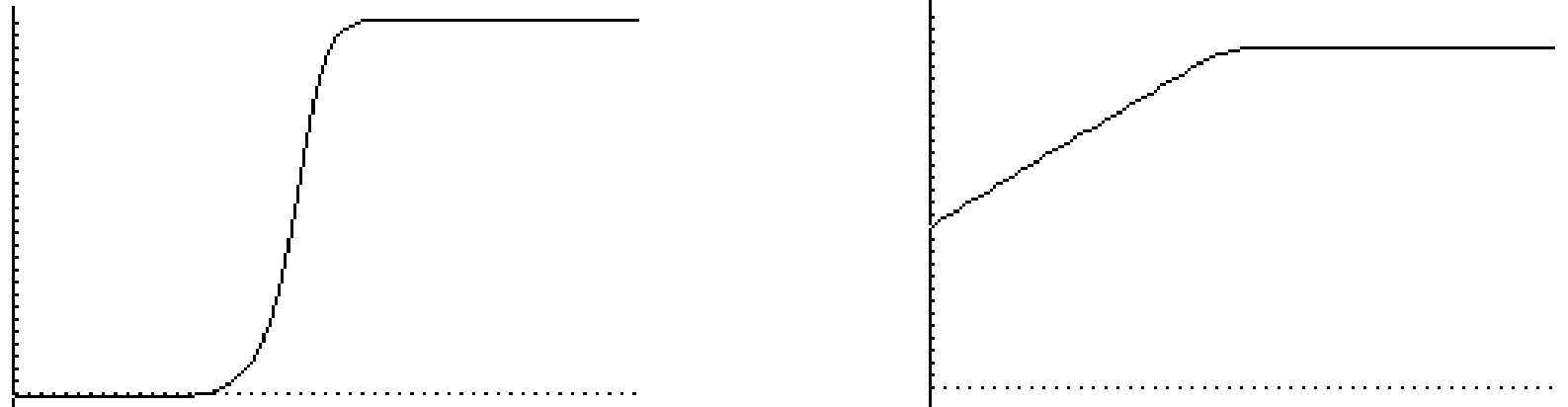
а б

Рисунок 2.18 Необходимо самостоятельно вывести все требуемые формулы для схем, предложенных на рисунке 2.15б, 2.17.