41. Переходные процессы в разветвленных электрических цепях (класс метод)

1.Из режима цепи до коммутации определяем независимые нач условия.U_C(0_)= U_C(0₊) i_L(0_)= i_L(0₊)

2. В момент времени t=0 записываем систему ур-ий для мгновенных токов и напряжений.

3. Для режима цепи после коммутации, определяем вид cв составляющей

U_C(t)=U_cnp+U_cCB: U_cCB=А₁е^р₁^t+ А₂е^р₂^t U_cCB=Ае^-tsin(_Ct+) U_cCB=(А₁+A₂)е^-t

4. Из режима цепи после коммутации определяем U_cnp

5. Исходя из нач условий, находим пост интегрирования А₁ и А₂

42. Преобразование Лапласа и его свойства

Прямое преобр-ие Л: ,

f(t)=А=const (ист эдс)

Обратное преобр-ие Л:

Cв-ва:

1.Cв-во линейности:

2.Cв-во дифференцирования:

43 З-ы Ома и Кирхгофа в опер. форме.

Алгебраическая сумма токов=0

44 Опер. Схемы замещения эл-в эл. Цепи. З. Ома в Оп. Форме для резистивного, индуктивного, емкостного эл.

рез. эл: Ur(t)=iR; Ur(p)=RI(p); Zr(p)=R; Ur(p)=Zr(p)I(p);

индук. эл: ; ; ; ; ; ;

ненул нач условия

емк. эл: ; ; ; ; ; .

Ненулевые нач условия Нулевые нач условия

46. Переходные процессы в разветвленных эл цепях (операторный метод)

1.Определяем независ нач условия до коммутации(U_C(0),i_L(0))

2. рисуем операторную схему замещения для режима цепи после коммутации, в к-ой все токи заменяем их изображениями (i₁(t) I₁(p)), все сопротивления- операторными , все источники эдс заменяем их изображениями, включаем изображения i_L(0) U_C(0)

3. Определяем любым методом , записанным в операторной форме изображение искомой величины

4. Если полученные изображения явл-ся табличными, то оригинал нах-им из табл.; если не табличный – то находим по теореме разложения, в зав-ти от корней характеристич уравнения, они явл-ся полюсами полинома знаменателя

47 Теор. разложения

F2(p)=0

если p1, p2 – вещ. и различ. F(p)=F1(p)/pF3(p)

; ;

если p1,p2 – комплексносопр.

48. Операторные передаточные ф-ции

Операторные передаточные ф-ции- отношение изображения р-ции к изображению воздействия, подвешенного к цепи при нулевых нач условиях

- воздействие - р-ция

4 вида операторных передаточных ф-ций:

Если полоса передаточных ф-ций нах-ся в левой полуплоскости, эл цепь-устойчивая, если в правой - неустойчивая

50 Имп воздействия на эл цепи.

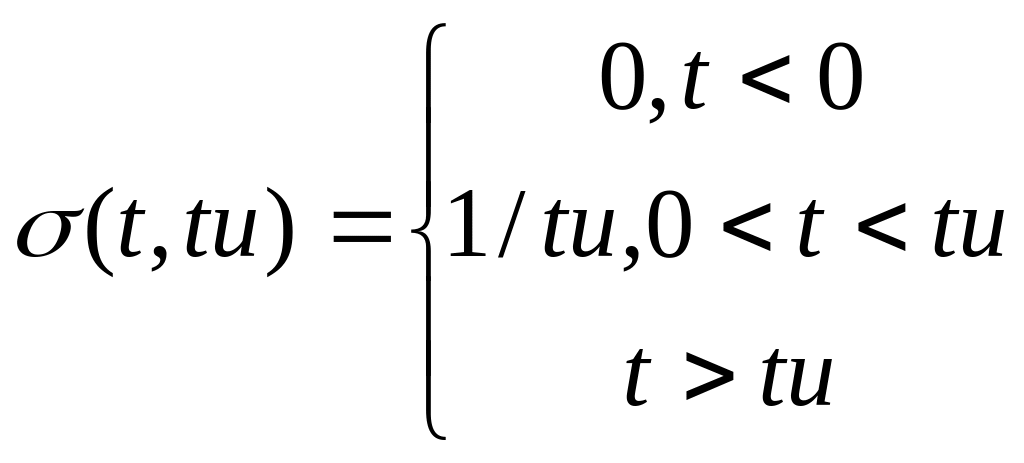
; Su=Etи=сonst; E=Su/tи=Su (t);

I= ;

f1(t)=Sи ; ; F1(p)=Su

51 имп реакции в эл цепях

Имп реакция – реакция эл цепи на имп воздействие.

H(p)=1/Zвх(p)=Yвх(p)

i(t)= ; Uc(p)=I(p)*1/pC= ;

52. Импульсные характеристики электрических колебаний

Su=1

F2(p)=H(p)F1(p)

f2(t)=g(t)Su g(t) H(p)

53. Интеграл наложения

При нахождении р-ции цепи с помощью интеграла наложения используется импульсная х-ка цепи g(t). Суммарная р-ция цепи на систему единичных импульсов:

Физ.смысл: входной сигнал f₁(x) взвешивается с помощью ф-ции g(t-x): чем медленнее убывает со временем g(t), тем большее влияние на вых сигнал оказывает более удаленные от момента наблюдения значение входного воздействия.

54. Переходные характеристики электрических цепей.

Отношение реакции эл.цепи на ступенчатое воздействие, подведенное к цепи при нулевых начальных условиях к величине этого воздействия, - переходные характеристики.

E=1 B

П.х. численно равна реакции эл. цепи на единичное ступенчатое воздействие, подведенное к цепи при нулевых начальных условиях.

f2(t) подобно U(t)

55. Интеграл Дюамеля

1.Непрерывная ф-ция

2. Кусочно-непрерывная ф-ция

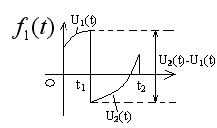
U(t)- воздействие

1 0<t<t₁

2.t₁<t<t₂

3.

56. Спектральный состав периодических колебаний. Спектры амплитуд и фаз периодического колебания

- периодическая

Обратное преобр-ие Фурье:

прямое пребр-ие Фурье:

Спектр ,в показат-ой: , где

Модуль: определяет амплитудный, а аргумент - фазовый спектр сигнала.

57. Частотный состав непериодического колебанияю Комплексная спектральная плотность колебания, спектральная плотность амплитуд и спектр фаз непериодич колебания.

- комплексная спектральная плотность сигнала. Спектральная плотность амплитуд:

58. Преобразование Фурье

Обратное преобр-ие Фурье:

прямое пребр-ие Фурье:

Спектр ,в показат-ой: , где

Модуль: определяет амплитудный, а аргумент - фазовый спектр сигнала.

59. Связь м/у временными и частотными х-ками эл цепи

Спектр вых сигнала:

Выходной сигнал

60 Нелин эл цепи. Графический метод расчета н.э.ц.

По виду ВАХ нелинейные элементы можно классифицировать на симм. и несимм.

Симм. наз-ся элемент у которого хар-ка не зависит от полярности приложенного напряжения.

НЭ можно разделить на упр-е и неупр-е.

Упр-й элемент имеет дополнит. цепь упр-я воздействуя на которую можно менять вид ВАХ.

Графический расчет цепей с последовательным соединением НЭ

U=U1+U2

Графический расчет цепей с параллельным соединением НЭ. Для расчета заданы ВА-характеристики: I₁(U₁), I₂(U₂), I(U). I=I₁+I2

Задан общий ток I, нужно рассчитать токи I₁ и I₂ и общее напряжение U. В этом случае необходимо построить суммарную характеристику, т.е. зависимость I(U). Для получения этой характеристики суммируем ординаты характеристик НС₁ и НС₂ (I₁(U₁) и I₂(U₂)).

последовательно-параллельным соединением НЭ. Заданы ВА-характеристики: I₁(U₁), I₂(U₂), I₃(U₃). Определить

I₁, I₂, I₃, U₁, U_ab.

Суммируем хар-ки I₂(U₂) и I₃(U₃) как при параллельном соединении. Получим последовательную цепь, где НС₁ соединен с эквивалентным сопротивлением НС₂₃.

U_ab=U₂=U₃; I₁=I₂+I₃;

Применим второй способ расчета, для этого построим ВА-характеристику нелинейного двухполюсника (НД) содержащего источник и НС₁. Это зависимость I₁(U_ab).

U_ab=U-U₁; I₁(U-U₁);

Рабочая точка (a) лежит на пересечении I₁(U-U₁) с U_ab(I₂+I₃).

U₁=U-U_ab