27 Полосовой и заграждающий фильтр

ПФ

«Г»

«Т» «П»

ЗФ

«Г»

«Т» «П»

28. Переходной установившийся режимы. З-ны коммутации

Переходной процесс- процесс перехода эл цепей из одного установивш-ся режима в другой.

Установившийся режим – режим, при к-ом токи и напряжения либо не знав-ят от времени (режим пост тока), либо периодически зав-ят от времени (не/синусоид-ый)

Переход процесс возникает в цепях, содержащих реактивные эл-ты (L,C), в к-ых может запасаться энергии.

П.п. возникает сразу же после коммутации, коммутация ос-ся с помощью ключа, в разомкнутом состоянии R= , в замкнутом состоянии =0

Коммутация – включение, отключение источника питания или элементов эл цепи, а также переходной процесс может быть обусловлен видом входного сигнала.

Расчет переходного процесса основан на 2-х з-нах коммутации:

1-ый з-н коммутации: ток в катушке не может изменяться скачком, т.к. энергия магнитного поля катушке не может изменяться скачок

2-ой з-н коммутации: напряжение на конденсаторе не может изменяться скачком, т.к. энергия эл пол конденсатора не может изменяться скачком - независим нач условия, все остальные величины в t=0 наз зависимыми нач условиями и опред-ся из ур-ий Кирхгофа, записанных для момента времени t=0

29. Переходной процесс при включении rl- цепи к источнику пост напряжения (класс метод)

1) источник пост напряжения

Решением неод диф ур-я явл-ся сумма общего решения однородного и частного решения неоднородного

Общее решение однородного ур-я наз. свободной составляющей:

Частное решение неод ур-я наз принужденной составляющей:

З-н изменение тока в RL- цепи:

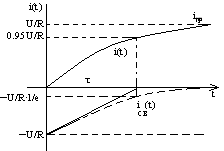
- время, в теч-ие к-ого свобод составляющей тока и напряжения изменяется в е раз – физич смысл

30. Переходной процесс при коротком замыкании в RL-цепи(класс метод)

- ненулевые начальные условия

UL+UR=0; L(diсв/dt)+iсвR=0;

τ=L/R t=0 U/(R+R0)=A

З-н изменения тока:

31 Переходной процесс при подключении RL цепи к источнику переменного синусоидального напряжения(класс метод)

iL(0_)=0

U(t)=U_mSin(ωt+φ_и); U_R+U_L=U(t);

; i(t)= i_св(t)+ i_пр(t) i_пр(t)=I_mSin(ωt+φ_и-φ);

φ=arctg(ωL/R);

τ=L/R; i(t)= I_mSin(φ_и-φ)+A; A= -I_mSin(φ_и-φ)

З-н изменения тока: i(t)=I_mSin(ωt+φ_и-φ)-I_mSin(φ_и-φ)e^-t/;

U_L(t)=U_mLSin(ωt+φ_и-φ+π/2); UmL=ImωL

UL(t)= U_mL Sin(ωt+φ_и-φ+π/2)+ U_mL R/(ωL)Sin(φ_и-φ)e^-t/τ- з-н изменения напряжения на катушке

_i/ п.п закончен

32 Переходной процесс при включении RC цепи к источнику постоянного напряжения (класс метод)

Uc+UR=U

UR=iR=RC(du\dt); RC(du_с\dt)+ Uc=U

Uccв=Ae^pt; (U_C-1; du_с\dt-p) pRc+1=0; p= -(1/RC) τ=RC; Uccв=Ae^pt=Ae^-(t/RC);

Uccв=Ae^-(t/RC) Uc_пр=U; Uc(t)=U+Ae^-(t/RC); Uc(0_)= Uc(0+)=0; 0=U+A; A=-U

Uc(t)=U(1-e^-(t/RC))

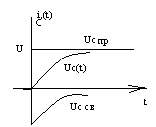
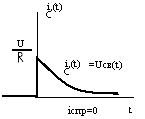
33 Переходной процесс при коротком замыкании RC цепи (класс метод)

Uc(0_)= Uc(0+)=0;

Uc+U_R=0 UR=iR=RC(du\dt); RC(du\dt)+ Ucсв Uc(t)=Uccв(t)=Ae^pt; pRC+1=0;

p= -(1/RC) τ=RC; Uccв=Ae^pt=Ae^-(t/RC); ^U=A; Uc(t)=Ue^-(t/RC); Wc=(CU²)/2

ic(t)=C(du\dt)=(-U/R)e^-t/RC

34 Переходной процесс при подключении RCцепи к источнику переменного синусоидального напряжения (класс метод)

Uc(0_)=0

U(t)=UmSin(ωt+φи); UR+Uc=U(t); ;

U(t)= Uсв(t)+U_пр(t) U_пр(t)=Um_C Sin(ωt+φи-φ-π/2); φ=-arctg(1/ωCR);

τ=RC; Uc(t)= U_mcSin(ωt +φи-φ-π/2)+Ae^-t/τ

0=UmcSin(φи-φ-π/2)+A A= -UmcSin(φи-φ-π/2);

Uc(t)= U_mcSin(ωt +φи-φ-π/2)+Ae^-t/τ- UmcSin(φи-φ-π/2)

i_c(t)=I_msin(ωt +φи+φ)+CUmcSin /CR (φи-φ-π/2)e^-t/τ

35. Разряд емкости в RLC цепи (апериодический характер)

Наблюдается в конденсаторе, если R²>4L²/LC; R>R_КР; R_КР=2r;

r=корень(L/C) => корни вещественные и разные =>

U_C СВ=A1exp(p1t)+A2exp(p2t), где A1и A2 – пост интегрирования

t=0

Энергия большая – в виде тепла на резисторе, меньшая – магн поле катушки

36 Разряд емкости в RLC цепи (периодич процесс)

Наблюдается в конденсаторе, если R<R_КР. Тогда корни комплексно-сопряжённые, p1,2=-a±jw_СВ (a=R/2L – коэффициент затухания, w_СВ – частота свободных колебаний). Период свободных колебаний Tсв=2p/w_СВ.

U_C СВ=Aexp(-at)sin(w_СВt+Θ)

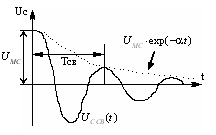
Энергия в конденсаторе: большая преобр-ся в энерг магн поля катушки, меньшая в тепловую

37. Разряд емкости в RLC цепях (критич х-р)

Наблюдается в конденсаторе, если R²/4L²-1/LC=0; R=R_КР, то есть R=R_КР=2r. Тогда p1=p2=p=-R/2L=--a.

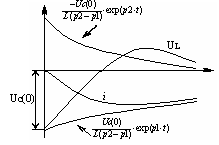
38 Включение RLC цепи на постоянное напряжение (апериодич процесс)

До коммутации конденсатор не заряжен и тока в цепи не было, т.е. имеем нулевые начальные условия.

u_c(0) =0 i₍₀₎=0

При замыкании рубильника начинается переходный процесс, кот. может иметь либо апериодический (R R_кр), либо колебательный характер(R R_кр).

1.Рассмотрим расчет при апериодическом характере.

u_c=u_cпр+u_ccв ; u_cпр=U ; u_cсв=A₁*e^P1t+A₂*e^P2t ;

u_c(0)=U+A₁+A₂ ; U+A₁+A =0; A₁=-p₂*U/(p₂-p₁);

uⁱc₍₀₎ =A₁p₁+A₂p₂ ; A₁p₁+A =0; A₂=p₁*U/ (p₂-p₁);

u_c=U+U*(-p₂*e^p1t+ p₁*e^p2t )/(p₂-p₁)

2.Рассмотрим колебательный характер.

u_c=u_cпр+u_ccв;

u_c=U+Ae^{- t}sin(w₀t+ );

u_c(0)=U+Asin ; U+Asin =0 ; A=-U/sin =-U/(w₀ LC)

uⁱ_c(0)=- Asin +w₀Acos ; - Asin +w₀Acos =0 ;

u_c=U- U/(w₀ LC)e^{- t}sin(w₀t+ );

Из графика видно , что в переходном режиме ,напряжение на емкости может почти в 2 раза превышать напряжение источника