8.4.5. Дифференциальное уравнение теплопроводности

Рассмотрим тепловое состояние элементарного куба с размерами ребер, параллельных координатным осям OX, OY, OZ: ΔX, ΔY, ΔZ (см. рис.8.15).

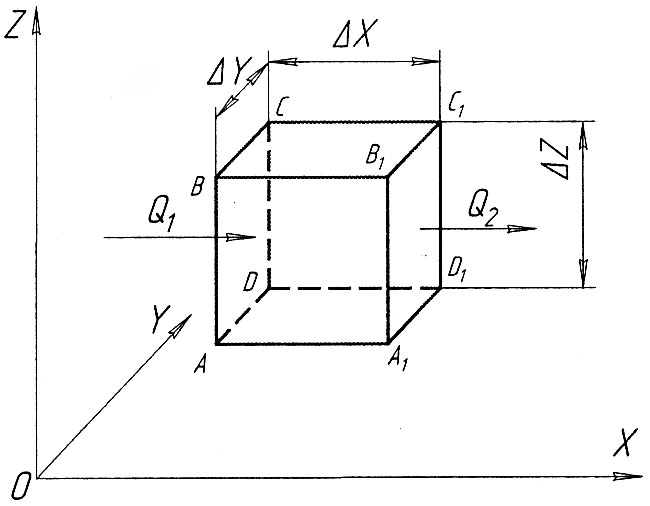
Рис.8.15. К выводу дифференциального

уравнения теплопроводности

Пусть за время Т через грань ABCD в куб входит за счет теплопроводности Q₁ количества тепла, а через грань A₁B₁C₁D₁ выходит количество тепла Q₂. Поскольку тепловой поток направлен на рис.8.15 слева направо и совпадает с положительным направлением оси OX, то температура на левой грани превышает температуру на правой. Пусть температура правой грани A₁B₁C₁D₁ равна θ, тогда температура на левой грани ABCD будет

Количество тепла, входящего через грань ABCD,

.

Количество тепла, уходящего через грань A₁B₁C₁D₁,

.

Количество тепла, остающегося в кубе, составит

.

Аналогично можно определить количество остающегося в кубе тепла за счет притока и оттока его через грани, перпендикулярные координатным осям ОУ и OZ

.

Общее количество накопленного в кубе тепла за время :

(8.7)

Данное тепло приведет к повышению температуры на величину дθ, определяемую выражением

где С - удельная теплоемкость материала куба, Дж/г.град;

ρ – плотность материала, г/см³.

Заменив dQ выражением (8.7), получим

. (8.8)

Величина ω = λ/Сρ называется коэффициентом температуропроводности. Она является константой вещества и характеризует скорость выравнивания температуры.

Уравнение теплопроводности может быть записано в следующем виде:

,

где Δ² - оператор Лапласа:

.

Если источник тепла, создающий тепловые потоки в элементарном кубе (см. рис.8.15), движется относительно него, то уравнение теплопроводности имеет следующий вид:

где V_X, V_y, V_Z - проекции на оси координат вектора скорости движения источника.

Для двухмерного температурного поля имеем

Для одномерного температурного поля:

Для стационарного трехмерного температурного поля

8.4.6. Условия однозначности при решении дифференциального уравнения теплопроводности

При выводе уравнения теплопроводности (8.8) не накладывалось каких-либо ограничений на форму тела и условия его взаимодействия с окружающей средой. Поэтому оно справедливо для тел любой формы. Однако при решении конкретных задач необходимо отразить конкретные исходные данные и выделить из множества возможных решений дифференциального уравнения то единственное, которое относится к данной конкретной задаче. Эти частные особенности, дополняющие и конкретизирующие дифференциальное уравнение теплопроводности применительно к конкретной задаче, называют условиями однозначности. Они включают начальные и граничные условия.

Начальные условия, определяющие тепловую ситуацию в рассматриваемом теле в момент времени, принятый за начало отсчета.

Граничные условия - это описание температурного поля или условий теплообмена на поверхностях тела с окружающей средой и другими телами. Граничные условия включают:

1. Параметры, характеризующие форму, размеры, теплофизические характеристики тела, в котором происходит процесс теплопроводности.

2. Параметры, характеризующие форму, размеры и мощность источников или стоков тепла, действующих в рассматриваемом процессе.

Начальные условия описываются зависимостями следующего вида:

T = 0, θ = f(X, Y, Z).

Часто температура в начальный момент равна температуре окружающей среды, которая известна:

T = 0, θ(X, Y, Z) = θ₀

Многообразие граничных условий, встречающихся на практике, может быть объединено в четыре группы: граничные условия первого рода (ГУ1), второго рода (ГУ2), третьего рода (ГУ3) и четвертого рода (ГУ4). Применительно к этим четырем видам граничных условий разработан достаточно полный математический аппарат, пригодный для решения многих практических задач.

Граничные условия первого рода заключаются в том, что известен закон распределения температуры на граничных поверхностях рассматриваемого тела, т.е. известны функции распределения температуры на поверхностях тела:

θ_S (X, Y, Z, Т) = 0.

Граничные условия второго рода выражаются в том, что известны законы распределения плотности тепловых потоков, проходящих через граничные поверхности:

q = f (X, Y, Z, Т).

Граничные условия третьего рода применяются в том случае, когда происходит теплообмен поверхности с окружающей средой. В этом случае граничные условия выражаются в том, что задается температура окружающей среды, с которой соприкасается рассматриваемое тело, и коэффициент теплообмена α [Вт/см²град] между средой и поверхностью. Согласно закону Ньютона-Рихмана, плотность теплового потока, проходящего через граничные поверхности тела, окруженного средой, пропорциональна разности температуры поверхности тела θ_S и температуры окружающей среды θ₀:

q = α (θ_S - θ₀).

Данный тепловой поток от поверхности тела должен компенсироваться тепловым потоком внутри тела направленным к его поверхности тела и определяемого по закону Фурье:

.

Данное выражение представляет собой математическое описание граничных условий третьего рода.

Граничные условия четвертого рода применяются тогда, когда рассматриваемое тело находится в плотном, беззазорном контакте с другим твердым телом, и между ними происходит теплообмен. При этом температуры на контактных поверхностях тел являются одинаковыми.

При решении конкретных задач на различных участках рассматриваемого тела могут встречаться различные граничные условия.

Различают пассивные и активные граничные поверхности.

К активным относят те граничные поверхности, условия теплообмена на которых оказывают существенное влияние на температуру рассматриваемой области твердого тела.

Пассивные – это такие поверхности, на которых температура и ее градиент в течение всего теплового процесса изменяются незначительно и не оказывают существенного влияния на температуру рассматриваемой области твердого тела.

Например, на рис.8.16 показана схема шлифования пластинки толщиной h. При малой толщине h граница А является активной, так как оказывает существенное влияние на температуру в пластинке. При большой толщине границу А можно будет считать пассивной, так как она не будет оказывать влияния на температуру. Пассивная граница может быть условно отодвинута на любое расстояние. Ей можно придавать любую форму, отличную от фактической.

Рис.8.16. Пассивная граничная поверхность

при шлифовании пластины