7.8.3. Расчет сил, действующих при обработке фрезами с винтовыми зубьями

В расчетах применяются проекции силы, действующей на фрезу: на ось фрезы - осевая сила P₀, на нормаль к обработанной поверхности - вертикальная сила P_V, на направление подачи - горизонтальная сила P_H.

В расчете последовательно определяют:

1. Параметры фрезы: d, d₀, B_Ф, Z, ω по соответствующему стандарту или чертежу фрезы; t – глубину резания.

2. Осевой шаг зубьев фрезы P = (πd ctg ω) / Z.

3. Угловой шаг зубьев η = 2π/Z, рад.

4. Угол контакта по формуле Ψ₀ = arccos (1 – 2t/d).

5. Количество одновременно работающих зубьев фрезы Z₀=Ψ₀/η + B/p, где b - ширина фрезерования. Полученное значение округляют до ближайшего большего целого числа.

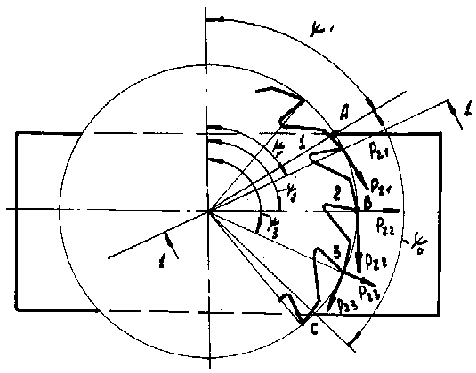
6. Номер наиболее загруженного зуба - N для того момента, когда угол выхода одного зуба равен углу контакта N = Ψ₀/η. Полученное значение округляют до ближайшего большего целого числа. Положение зуба на дуге контакта фрезы с заготовкой задается двумя углами, определяющими положение режущих кромок в двух торцовых сечениях заготовки. Большой угол называется углом выхода и обозначается Ψ'', а меньший - углом входа и обозначается Ψ'. Номер зуба, которому относятся эти углы, обозначается индексом i.

7. Углы входа Ψ_i' и углы выхода Ψ_i'' для всех работающих зубьев для случая, когда силы, действующие на фрезу, максимальны. Этот случай соответствует рис.7.27.

Для зубьев с номером i < N угол входа Ψ_i'=Ψ₀–(2B tg ω)/d–(N–i)η; угол выхода Ψ_i'' = Ψ₀– (N – i)η.

Для зубьев с номером i > N угол вхoда Ψ_i'=Ψ₀–[2(B–P)/d]tgω(i–N); угол выхода Ψ_i'' = Ψ₀.

Если какой-либо угол входа Ψ_i' получается отрицательным, то его принимают равным нулю.

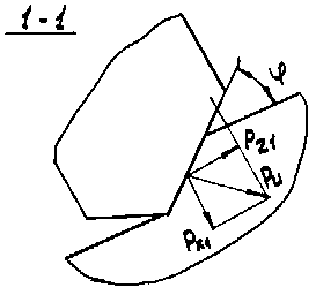
8. Углы расположения центров тяжести сечения срезаемых слоев на дуге контакта для каждого зуба

Ψцi =	Ψi'2 + Ψi''2 + Ψi'Ψi''
	3 (Ψi' + Ψi'')

9. Толщины срезаемых слоев в поперечных сечениях фрезы, проходящих через центры тяжести сечений срезаемых слоев: a_цi = S_z sin ψ_цi

Рис.7.27. Силы, действующие при

обработке фрезой с винтовыми зубьями

10. Действительные передние углы зубьев фрезы, для которых a_цi < r:

.

11. Главную составляющую силы резания, направленную по вектору скорости резания, действующую на i - тый зуб, по зависимости (7.31), в которой применительно к обработке фрезой с винтовым зубом необходимо произвести следующую замену:

ab =	d Sz	(cos Ψi' – cos Ψi'').
	2 sin ω

Применительно к данному случаю зависимость (7.31) приобретает вид

PZi =	τdSz (cosΨi' – cosΨi'')(cos γi + tg ρi cos ω sin γi + tg ρi sin ω tg ω)	+ μЗQ
	2 sin ω sin βNi [cos (βNi - γNi) – tg ρ cos ω sin(βNi – γi)]

12. Радиальную составляющую силы резания, направленную по радиусу фрезы, действующую на i - тый зуб, по зависимости (7.32), которая после вышеуказанной замены произведения ab приобретает вид:

    Pyi =	τdSz (cosΨi' – cosΨi'')(tg ρi cos γi cos ω - sin γi)	+ Q
    	2 sin ω sin βNi [cos (βNi - γi) – tg ρ cos ω sin(βNi - γi)]

13. Осевую составляющую силы резания, направленную по оси фрезы, действующую на i - тый зуб, по зависимости (7.33), которая после вышеуказанной замены произведения ab приобретает вид:

    PXi =	τdSz (cosΨi' – cosΨi'')(cos γi sinω + tg ρi sin γi sin ω cosω - tg ρi sinω cosω)
    	2 sin ω sin βNi [cos (βNi - γi) – tg ρ cos ω sin(βNi - γi)]

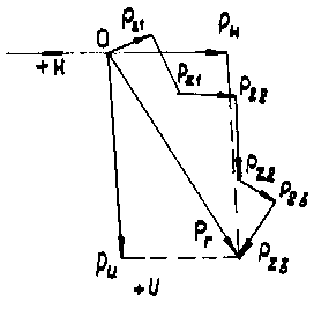
14. Силы, действующие на фрезу и заготовку: горизонтальная сила, параллельная направлению подачи

(7.40)

вертикальная сила, действующая в направлении, перпендикулярном плоскости стола горизонтально-фрезерного станка:

(7.41)

В формулах (7.40), (7.41) верхние знаки относятся к встречному фрезерованию, нижние - к попутному.

Осевая сила, действующая в направлении, параллельном оси фрезы

15. Равнодействующая сила, приложенная к фрезе

.

16. Расчетный крутящий момент

.

а
б	в
Рис.7.28. Силы, действующие при торцовом фрезеровании: а – силы, действующие в плоскости, перпендикулярной оси фрезы; б – разложение нормальной силы на радиальную и осевую; в – план сил