5.5.2. Относительный сдвиг

Является характеристикой деформации простого сдвига, схема которого показана на рис.5.8а. Если на короткий стержень ABCD, закрепленный основанием AD, подействовать сдвигающей силой Т, то стороны его AB и CD повернутся на угол Ψ, и произойдет деформация простого сдвига. Механизм этой деформации легко уяснить, используя аналогию деформации колоды игральных карт, когда каждая карта, расположенная сверху, сдвигается относительно соседней нижней карты на одну и ту же величину. Относительный сдвиг определяется по формуле (см. рис. 5.8)

.

Применение относительного сдвига в качестве характеристики деформации срезаемого слоя основано на том, что любая пластическая деформация, в том числе и в процессе резания, происходит путем многочисленных сдвигов под действием касательных напряжений.

Для определения относительного сдвига по параметрам процесса резания выделим в срезаемом слое 1, по аналогии с рис.5.8, элемент ABCD (см. рис.5.14) так, чтобы точка С лежала на поверхности срезаемого слоя. В результате пластической деформации прямоугольник ABCD преобразуется в параллелограмм AB₁C₁D, поверхность МК срезаемого слоя переходит в поверхность KC₁FC₂F₂ стружки, а точка С переходит в точку С₁. Абсолютный сдвиг при этом равен отрезку СС₁. Пластическая деформация происходила во время перемещения точки С в точку С₁. Дальнейшая деформация происходила путем частичного разрушения стружки с разделением материала в точке С₁. Отрезок С₁F соответствует величине скольжения верхней части стружки относительно нижней на стадии разрушения.

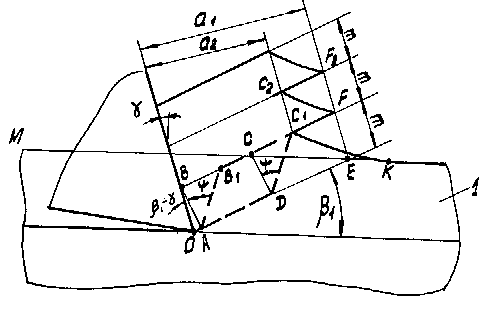
Рис.5.14. Деформация простого сдвига элемента

срезаемого слоя ABCD при образовании стружки

Относительный сдвиг определяется из рис.5.14:

ε = tgΨ = CC₁/CD, CC₁ = BC₁ – BC;

BC₁ = a₂/cos (β₁ – γ), BC = OE – DE – OA;

OE = a₁/cos (β₁ – γ), CD = m cos (β₁ – γ);

DE = CD ctg β₁ = m cos (β₁ – γ) ctg β₁;

OA = m sin (β₁ – γ).

В итоге получим

. (5.4)

Часто на практике выступы на внешней стороне стружки незначительны, ими можно пренебречь, а стружку принять за сливную.

Для сливной стружки имеем а₁ = а₂:

. (5.5)

Выразим относительный сдвиг через усадку для сливной стружки, применив формулу (5.3):

.

Выполнив упрощающие преобразования, получим

.

Обычно на практике передний угол изменяется незначительно: -20° < γ < +20°, поэтому можно принять sin γ ≈ 0, cos γ ≈ 1. Тогда получим

,

т.е. чем больше усадка, тем ближе она к относительному сдвигу. При с ошибкой не более 6,3% можно принять . Отсюда можно сделать вывод, что для малых степеней деформации усадка не является характеристикой пластической деформации в процессе резания и лишь усадка, превышающая , может служить характеристикой деформации при резании.

5.6 Прогнозирование вида и размеров стружки при резании металлов

При обработке металлов резанием в зависимости от конкретных факторов образуются различающиеся внешними признаками сливные, суставчатые, и элементные стружки надлома. Однако предсказать априори вид образующейся стружки весьма затруднительно. Прогнозирование вида стружки и ее параметров имеет не только теоретическое, но и практическое значение. При проектировании технологических систем механической обработки в автоматизированном производстве необходимо обеспечить отвод стружки из зоны обработки и транспортировку ее от оборудования, что связано с необходимостью ее дробления. Различная склонность к дроблению вышеуказанных стружек обусловливает различные технические решения, основанные на прогнозировании вида стружек и их параметров.

Образование стружки того или иного вида, как уже было сказано в 5.4, определяется соотношением необходимой (потребной) и предельной деформаций.

Необходимая деформация при обработке резанием – это величина деформации, которую нужно сообщить срезаемому слою, расположенному параллельно вектору скорости резания, для того, чтобы преобразовать его в стружку некоторой толщины, расположенную параллельно передней поверхности лезвия режущего инструмента. Она оценивается относительным сдвигом, определяемым углом сдвига β₁ и передним углом лезвия инструмента  по известной зависимости (5.5):

_н = ctg β₁ + tg (β₁  ).

Предельная деформация, которая оценивается предельным относительным сдвигом _пр  это наибольшая величина пластической деформации, происходящей в процессе образования стружки, которую может выдержать обрабатываемый материал в конкретных условиях деформирования без разрушения, т.е. без нарушения его сплошности и образования новых поверхностей на внешней поверхности стружки.

Предельная деформация определяется природой обрабатываемого материала, его состоянием (структурой, размером зерна, параметрами кристаллической решетки, степенью предварительной деформации), скоростью деформации, температурой, схемой деформации и др. Ее можно определить после свершения пластической деформации, доведенной до разрушения образца из обрабатываемого материала. При резании металлов, когда срезаемый слой был подвергнут деформации, величина которой превышала предельную, о чем могут свидетельствовать образованные в результате деформации разрушения впадины на внешней поверхности стружки, предельная деформация может быть определена по результатам измерения размеров стружки и зависимости (5.4):

_пр = ctg β₁ + tg (β₁  )  .

Для элементной стружки а₂  0 и правая часть зависимости тождественно равна нулю, что соответствует экспериментальным данным, свидетельствующим о том, что элементные стружки образуются при _пр  0.

Однако при проектировании технологических систем размеры стружки, как правило, неизвестны, и возможна лишь приблизительная оценка предельной деформации, которая затрудняется тем, что механизм образования стружки не является постоянным, а изменяется при изменении факторов процесса резания. Наибольшее влияние на изменение характера стружкообразования оказывает скорость резания в связи с наибольшим влиянием ее на температуру и скорость деформации. При скоростях резания, определяющих температуру на плоскости сдвига, не превышающую 0,25 температуры плавления обрабатываемого материала, характерную для обработки резанием, физико-механические характеристики которого при этом практически не отличаются от характеристик, полученных при стандартных механических испытаниях образцов из обрабатываемого материала, представляется возможным использовать эти характеристики для количественной оценки предельной деформации при резании. Наиболее приемлемой характеристикой для оценки предельной деформации материала при невысоких скоростях и температурах деформации является относительное сужение _ш в шейке образца из обрабатываемого материала в момент разрыва при испытаниях на растяжение. Предельная деформация сдвига в шейке образца определяется [5] относительным сужением обрабатываемого материала ψ_ш:

е_ш = .

Предельная деформация при резании определяется с учетом коэффициента жесткости напряженного состояния [5]:

_пр = 2 е_ш ехр (0,72 П), (5.6)

где П = (₁ + ₂ + ₃) / _i – коэффициент жесткости напряженного состояния в зоне стружкообразования; ₁, ₂, ₃  главные нормальные напряжения; _i – интенсивность напряжения.

Для зоны стружкообразования необходимо определить значение П для граничной точки А условной плоскости сдвига (см. рис.5.15), соответствующей наиболее вероятному очагу разрушения, в которой действуют нормальные и касательные напряжения, возникающие от действия нормальной силы N и силы трения F, приложенных на передней поверхности лезвия, производящих внецетренное сжатие и изгиб элемента стружки.

Напряженное состояние в зоне стружкообразования является плоским и характеризуется нормальными напряжениями _А и касательными ₂. В окрестности точки А (см. рис.5.15) нормальное напряжение _А определяется из условия изгиба прилежащего к плоскости сдвига АВ элемента стружки силами N и F и сжатия под действием нормальной силы Р.

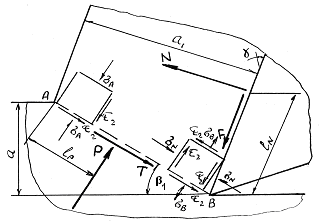
Рис. 5.15 Силы и напряжения, действующие

в зоне стружкообразования

Из рис.5.15 получили следующее выражение:

_А = ,

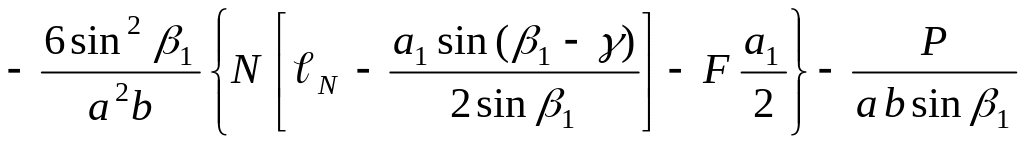где F и N  соответственно сила трения и нормальная сила на передней поверхности инструмента; Р  нормальная сила на плоскости сдвига; – расстояние от режущей кромки до точки приложения силы N.

Из условия равновесия сил, действующих на стружку, получили

N = ;

Р =

где  - угол трения стружки по передней поверхности режущего инструмента, определяемый по методике, изложенной в 5.14.

Интенсивность напряжений в точке А: _iA = .

Коэффициент жесткости напряженного состояния

П_А = .

При _н  _пр образуется сливная стружка, при _н > _пр  суставчатая, и необходимо определить размеры стружки: шаг выступов m, толщину стружки по впадинам а₂. Для этого необходимо рассмотреть механизм образования элемента стружки.

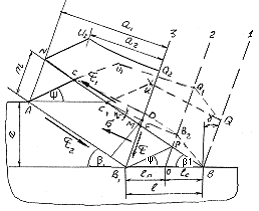
Рис. 5.16 Стадии образования суставчатой стружки

На рис.5.16 цифрами 1, 2, 3 обозначены положения передней поверхности лезвия инструмента, соответствующие различным стадиям образования суставчатой стружки. В поз. 1 завершено образование элемента BQUC₁. При перемещении лезвия на расстояние из поз. 1 в поз. 2 происходит деформация пластического сжатия материала срезаемого слоя, расположенного впереди лезвия, которая распространяется в некотором объеме срезаемого слоя, прилежащего к передней поверхности лезвия. При этом можно предположить, что  ОРВ трансформируется в равновеликий ему  С₁В₂Р. Ранее образованный элемент стружки BQUC₁ скользит при этом по плоскости сдвига ВС₁, поворачиваясь против часовой стрелки на некоторый угол , и занимает в итоге положение B₂Q₁U₁C. Точка С₁ срезаемого слоя при этом неподвижна, а точка С элемента BQUC₁ перемещается на расстояние С₁С. В поз. 2 сила, действующая на срезаемый слой, достигает величины, достаточной для протекания пластической деформации в некотором объеме срезаемого слоя. При движении лезвия из позиции 2 в позицию 3 происходит простой сдвиг – поворот элемента срезаемого слоя ОВ₁АС₁В₂ на угол , соответствующий значению предельной деформации сдвига _пр. Из рис.5.16 в соответствии с вышеизложенным получена следующая зависимость для угла ψ:

tg ψ = .

Для сливных стружек _пр = _н, tg ψ = ctg , ψ = 90  , для элементных _пр = 0, ψ = 0.

Размеры элемента стружки можно определить из условия равновесия элемента стружки В₁АСD (рис.5.16) в конечной стадии его образования, которое имеет вид

₁ CF +  DB₁ cos (β₁  )   DB₁ sin (β₁ )  ₂ = 0. (5.7)

Из рис 5.16. получили следующие выражения:

CF = ; DB₁ = ;

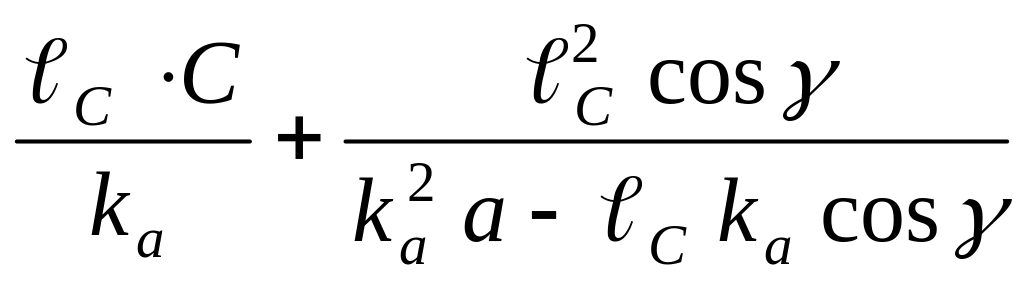C = ; K =  cos (β₁  )   sin (β₁  ).

После некоторых преобразований и обозначений уравнение (5.7) запишется в следующей форме:

А  В ℓ_С  D = 0 (5.8)

А = ;

В =

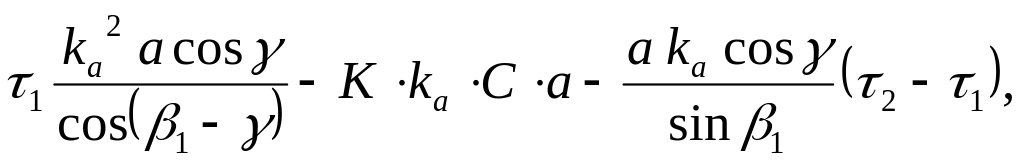
D = ,

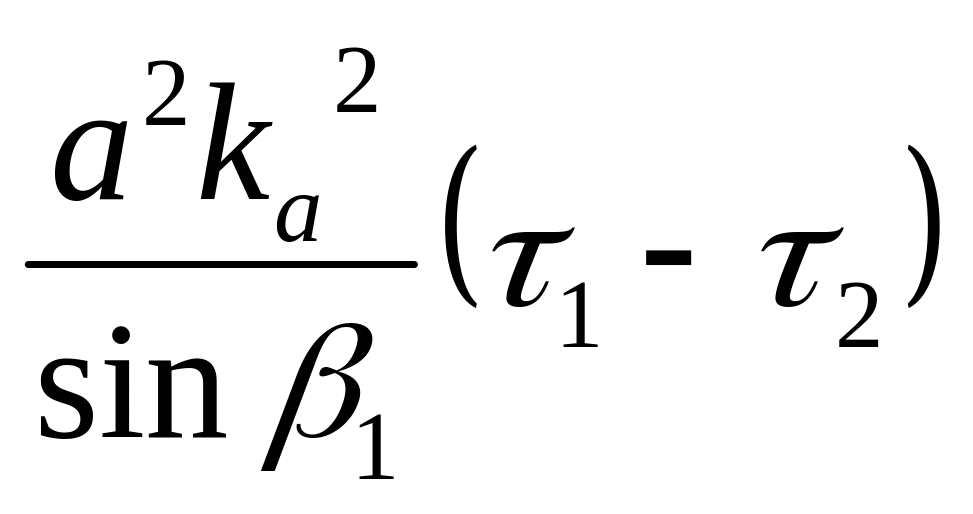где ₁, ₂  соответственно касательные напряжения на верхней и нижней границах элемента стружки;  и   соответственно нормальное и касательное напряжения на передней поверхности инструмента непосредственно у режущей кромки.

При этом можно принять следующие соотношения [3]:

₂ = 0,5 S_k + ₁ _A;  = 0,5 S_k; ₁ = 0,9 ;  = 2 _в

где S_k  истинный предел прочности, определяемый по зависимости S_k = _в (1 +  + _ш);  и ψ_ш - соответственно относительное удлинение и сужение при испытаниях обкатываемого материала на растяжение; ₁  коэффициент внутреннего трения, который для сталей может быть принят ₁ = 0,15; _в – предел прочности при растяжении обрарабатываемого материала.

Приемлемым для данной задачи является следующее решение уравнения (5.8):

.

По величине определяются размеры стружки:

- толщина по впадинам а₂ = а К_а  cos  ;

- толщина по выступам а₁ = а К_а ;

- шаг элемента стружки по выступам

m = .

Коэффициент утолщения стружки определяется по зависимости К_а = , а угол сдвига β₁ = , ₁ = arctg ₁.

По приведенным выше зависимостям для стали при _ш = 0,5;  = 0,1, _в = 50 кг/мм² вычислили _н, _пр, К_а и отношение , по которым построили зависимости вышеуказанных величин от переднего угла (см. рис.5.17). Из рис. 5.17 следует, что предельная деформация при изменении переднего угла от 60 до +80 уменьшается от 1,8 до 0,8 (линия 3), в то время как необходимая (линия 1) - от 8 до 0,1. При 60 <   50 образуется элементная стружка и = 0 (линия 4), при 50 <   +40  суставчатая стружка, так как при этом отношение (линия 4) возрастает от 0 до 1; при  > +40 образуется сливная стружка.

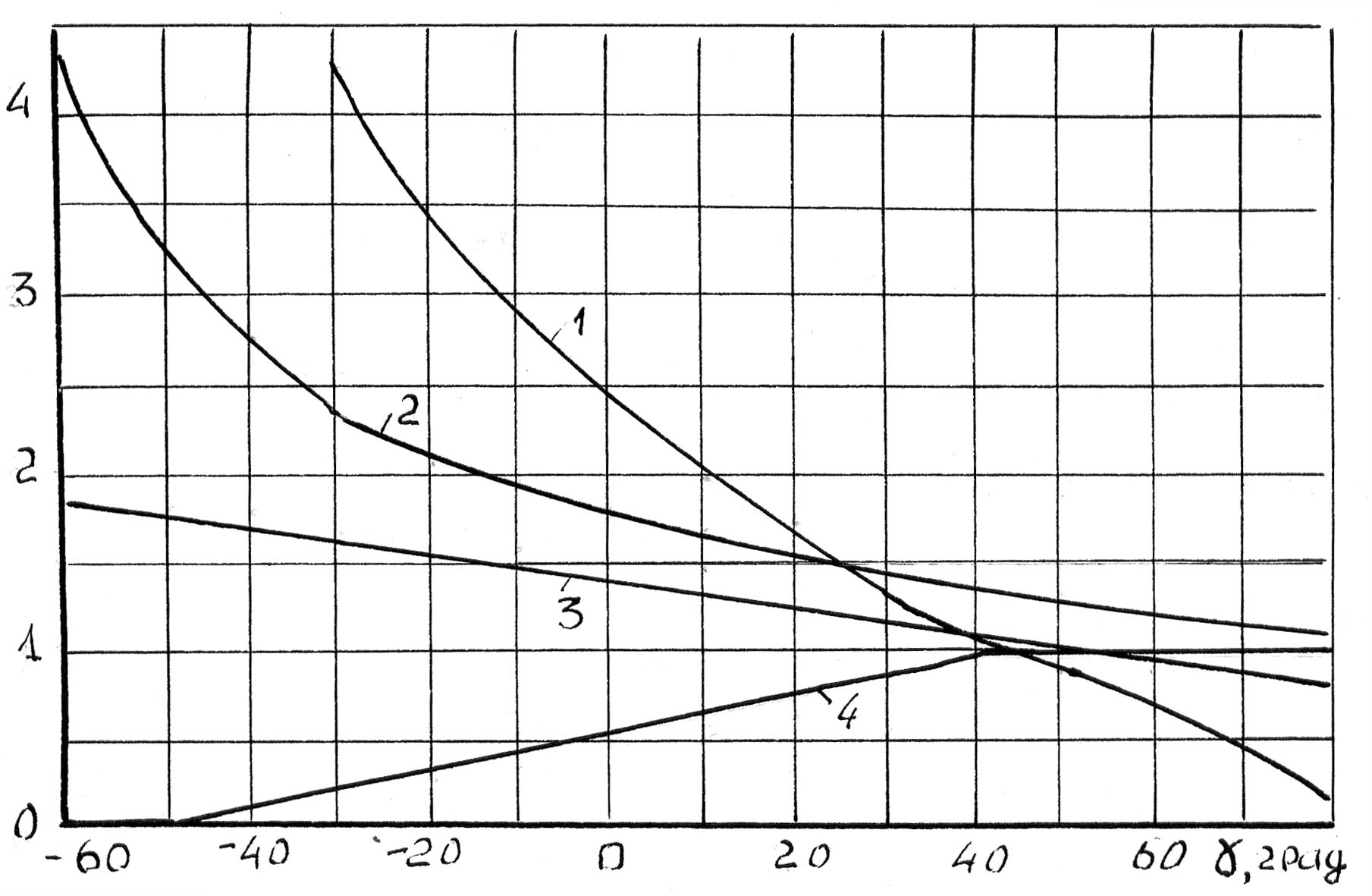
Рис.5.17 Влияние переднего угла режущего инструмента

на характеристики стружкообразования при обработке стали:

при ψ_ш = 0.5, δ = 0.1, σ_В = 50 кг/мм², 1 – ε_н; 2 – К_а; 3 – ε_пр ; 4 – а₂/а₁

Приведенные здесь зависимости рекомендуются для расчета показателей стружкообразования при обработке резанием, когда процесс стружкообразования не сопровождается адиабатическим сдвигом, возникающим при скорости резания, определяемой эмпирической зависимостью

, м/с,

где   коэффициент теплопроводности для обрабатываемого материала, ; S_k  истинный предел прочности, кг/мм²; а  толщина срезаемого слоя, мм.