- •Введение
- •Основы теории резания материалов
- •1. Движения, происходящие при обработке резанием
- •2. Инструментальные материалы
- •2.1. Требования, предъявляемые к инструментальным материалам
- •2.2. Инструментальные стали
- •Углеродистые инструментальные стали
- •2.2.2. Легированные инструментальные стали
- •Быстрорежущие стали
- •2.3. Металлокерамические твердые сплавы
- •2.4. Дисперсионно -твердеющие сплавы
- •2.5. Минералокерамика
- •2.6. Сверхтвердые материалы (стм)
- •2.7. Выбор инструментального материала
- •3. Геометрия режущего инструмента
- •3.1 Общие сведения
- •3.2. Устройство проходного токарного резца
- •3.3. Общие понятия и определения
- •3.4. Геометрия проходного токарного резца
- •3.5. Назначение углов
- •3.6. Зависимости между углами, измеряемыми в различных координатных и секущих плоскостях
- •3.7. Влияние установки резца на станке на его геометрию
- •3.7.1. Резец повернут в основной плоскости
- •3.7.2. Резец смещен по вертикали от оси вращения шпинделя токарного станка
- •3.8. Влияние различных движений, составляющих движение резания, на геометрию
- •3.8.1. Влияние движения подачи
- •3.8.2. Влияние движения формообразования при нарезании резьбы резцом
- •3.8.3. Влияние вибрационного движения
- •3.9. Конструкция и геометрия спирального сверла
- •3.9.1. Конструкция
- •3.9.2. Геометрия
- •3.10. Геометрия фрез
- •3.10.1. Общие признаки
- •3.10.2. Цилиндрическая фреза с прямыми зубьями
- •3.10.3. Фреза с винтовыми зубьями
- •3.10.4. Торцовая фреза со вставными ножами
- •Элементы режима резания и геометрия срезаемого слоя
- •4.1. Общие понятия и определения
- •4.2. Строгание
- •4.2.1.Элементы режима резания
- •4.2.2. Геометрия срезаемого слоя
- •4.2.3. Геометрическая шероховатость
- •4.3. Точение
- •4.3.1. Режим резания
- •4.3.2. Геометрия срезаемого слоя
- •4.3.3. Геометрическая шероховатость
- •4.4. Обработка цилиндрической фрезой с прямыми зубьями
- •4.4.1. Элементы режима резания
- •4.4.2. Элементы фрезерования
- •4.4.3. Геометрия срезаемого слоя
- •4.4.4. Геометрическая шероховатость
- •4.5. Два вида фрезерования – попутное и встречное
- •4.6. Обработка цилиндрической фрезой с винтовыми зубьями
- •4.6.1. Элементы режима резания
- •4.6.2. Геометрия срезаемого слоя
- •4.7. Равномерное фрезерование
- •4.8. Торцовое фрезерование
- •4.8.1. Виды торцового фрезерования
- •4.8.2. Элементы режима резания
- •4.8.3. Элементы фрезерования
- •4.8.4. Геометрия срезаемого слоя
- •4.8.5. Геометрическая шероховатость
- •4.9. Круглое наружное шлифование
- •4.9.1. Понятие об абразивном инструменте
- •4.9.2. Кинематика и элементы режима резания
- •4.9.3. Толщина срезаемого слоя
- •4.10. Нарезание резьбы
- •4.10.1. Нарезание резьбы резцом
- •4.10.2. Нарезание резьбы гребенкой
- •4.10.3. Нарезание резьбы метчиками и плашками
- •4.10.4. Нарезание резьбы гребенчатыми фрезами
- •4.11. Сверление
- •4.12. Зенкерование и развертывание
- •5. Процесс образования стружки
- •5.1. Характеристика стружек
- •5.2. Механизм пластической деформации
- •В процессе пластической деформации
- •5.3. Механизм образования стружки
- •5.4. Причины образования различных стружек
- •5.9. Влияние угла сдвига на толщину стружки
- •5.5. Показатели деформации срезаемого слоя
- •5.5.1. Усадка
- •5.5.2. Относительный сдвиг
- •5.6 Прогнозирование вида и размеров стружки при резании металлов
- •5.7. Скорость деформации
- •5.7.1 Общие сведения
- •5.7.2 Оценка средней скорости пластической деформации при резании металлов
- •5.8. Исследование деформации срезаемого слоя методом координатных сеток
- •5.9. Зона стружкообразования
- •5.10. Влияние факторов процесса резания на деформацию срезаемого слоя
- •5.11. Внутреннее строение стружки
- •5.12 Определение угла текстуры стружки
- •5.13. Определение угла сдвига
- •5.14. Определение среднего коэффициента трения при резании металлов
- •5.15 Оценка предельного значения угла сдвига при резании материалов
- •6. Явления, сопутствующие процессу резания и влияющие на качество обработки
- •6.1. Общая характеристика
- •6.2. Нарост
- •6.3. Образование остаточных напряжений
- •6.4. Влияние остаточных напряжений на эксплуатационную прочность деталей машин
- •6.5. Измерение остаточных напряжений
- •6.6. Вибрации при резании металлов
- •6.7. Вибрационное резание
- •6.8. Деформационное упрочнение (наклёп)
- •7. Силы резания
- •7.1. Значение вопроса
- •7.2. Силы, действующие на лезвие проходного токарного резца
- •7.3. Эмпирические формулы для расчета сил резания
- •7.4. Удельное давление резания
- •7.5. Соотношение между составляющими силы резания
- •7.6. Экспериментальное исследование сил резания
- •7.6.1. Принцип измерения сил и типы динамометров
- •7.6.2. Методика проведения эксперимента
- •7.6.3. Обработка результатов измерения
- •7.7. Расчет сил, действующих на лезвие инструмента
- •7.7.1. Постановка вопроса
- •7.7.3. Расчет сил, действующих по задней поверхности лезвия
- •7.7.4. Теоретические формулы для расчета составляющих силы резания
- •7.7.5 Прогнозирование радиуса скругления режущей кромки инструмента
- •7.7.6. Расчет сил, действующих при косоугольном резании
- •7.7.7 Влияние угла наклона режущей кромки на главную составляющую силы резания
- •7.8. Определение расчетных нагрузок при проектировании элементов технологических систем
- •7.8.1. Общие положения
- •7.8.2. Расчет сил резания при обработке фрезами с прямыми зубьями
- •7.8.3. Расчет сил, действующих при обработке фрезами с винтовыми зубьями
- •7.8.4. Расчет сил, действующих при торцовом фрезеровании
- •7.8.5. Расчет сил, действующих при протягивании
- •7.8.6. Расчет сил, действующих при сверлении
- •8.3. Температура резания
- •8.4. Расчет температуры на контактных поверхностях лезвия режущего инструмента
- •8.4.1. Общие сведения
- •8.4.2. Понятие о температурном поле
- •8.4.3. Понятие о градиенте температуры
- •8.4.4. Основной закон теплопроводности
- •8.4.5. Дифференциальное уравнение теплопроводности
- •8.4.6. Условия однозначности при решении дифференциального уравнения теплопроводности
- •8.4.7. Схематизация формы и теплофизических характеристик тел, участвующих в теплообмене
- •8.4.8. Фундаментальное решение дифференциального уравнения теплопроводности
- •8.4.9. Описание формы тел и условий на граничных поверхностях с помощью системы отраженных источников
- •8.4.10. Конвективный теплообмен
- •8.4.10.1. Общие сведения
- •8.4.10.2. Теплоотдача при естественной конвекции
- •8.4.10.3. Теплоотдача при вынужденном движении жидкости или газа
- •8.4.10.4. Регулярный режим охлаждения
- •8.4.10.5. Теплообмен при изменении агрегатного состояния жидкости
- •8.4.10.6. Теплообмен при конденсации пара
- •8.4.10.7. Лучистый теплообмен
- •8.4.11. Расчет интенсивности источников тепла в зоне резания
- •Расчет средних температур на контактных площадках лезвия резца [25]
- •9. Износ и стойкость режущего инструмента
- •9.1. Природа и виды изнашивания режущего инструмента
- •9.2. Геометрия износа
- •9.3. Измерение износа инструмента
- •9.4. График износа инструмента. Понятие о стойкости инструмента и критерии его затупления
- •9.5. Зависимость стойкости от факторов процесса резания
- •9.6. Оптимальная стойкость инструмента
- •9.6.1. Постановка вопроса
- •9.6.2. Определение экономической стойкости
- •9.6.3. Определение стойкости, наибольшей производительности
- •9.7. Обрабатываемость резанием
- •9.8. Методы улучшения обрабатываемости материалов резанием
- •9.9. Прочность лезвия инструмента
- •9.9.1. Общие сведения
- •9.9.2. Хрупкое разрушение лезвия
- •9.9.3. Пластическое разрушение лезвия
- •10. Определение оптимального режима резания
- •10.1. Обоснование методики выбора элементов режима резания
- •10.2. Токарная обработка
- •10.2.1. Общие указания
- •10.2.2. Выбор геометрии режущей части
- •10.2.3. Глубина резания
- •10.2.4. Определение наибольшей технологически допустимой подачи
- •10.2.4.1. Определение подачи, допускаемой шероховатостью обработанной поверхности
- •10.2.4.2. Определение подачи из условия обеспечения заданной точности обработки
- •10.2.5. Выбор сечения стержня резца
- •10.2.6. Определение силы подачи
- •10.2.7. Определение скорости резания
- •10.2.8. Определение потребной мощности станка
- •10.2.9. Выбор станка
- •10.2.10. Определение параметров настройки токарного станка
- •10.3. Определение режима резания для многоинструментальной обработки
- •10.4. Фрезерование
- •10.4.1. Общие указания
- •10.4.2. Определение подачи
- •10.4.3. Определение скорости резания и выбор станка
- •10.5. Сверление
- •10.5.1. Общие рекомендации
- •10.5.2. Определение подачи
- •10.5.3. Определение скорости резания, мощности и силы подачи
- •10.6. Зенкерование и развертывание
- •10.6.1. Общие рекомендации
- •10.6.2. Определение подачи
- •10.6.3. Определение скорости резания, мощности станка и его настроечных данных
- •10.7. Шлифование
- •10.7.1. Общие рекомендации
- •10.7.2. Определение глубины резания
- •10.7.3. Выбор подачи
- •10.8. Нарезание резьбы
- •10.8.1. Общие указания
- •10.8.2. Нарезание резьбы резцами, плашками и винторезными головками
- •10.8.3. Нарезание резьбы гребенчатыми фрезами
- •10.8.4. Нарезание резьбы метчиками
- •10.9. Особенности обработки резанием пластмасс
- •Основные физико-механические свойства некоторых пластмасс
- •Рекомендуемые геометрические параметры режущего инструмента для обработки пластмасс резанием
- •Режимы резания при обработке пластмасс
- •11. Процессы физико-химической обработки
- •11.1. Общая характеристика физико-химических методов обработки (фхо)
- •11.2. Электроэрозионная обработка (ээо)
- •11.2.1. Общая характеристика ээо
- •11.2.2. Основные виды технологических процессов ээо
- •11.2.3. Оборудование для ээо
- •11.3. Электрохимическая обработка (эхо)
- •11.4. Ультразвуковая обработка материалов (узом)
- •11.5. Лучевая обработка
- •11.5.1. Лазерная обработка
- •11.5.2. Электронно-лучевая обработка
- •11.6 Комбинированные методы обработки (кмо)
- •Приложение
- •Библиографический список
- •Содержание
- •6. Явления, сопутствующие процессу резания и влияющие
- •Процессы механической и физико-химической обработки материалов
- •107077, Г. Москва, Стромынский пер., 4
3.6. Зависимости между углами, измеряемыми в различных координатных и секущих плоскостях
На чертежах некоторых инструментов: сверл, торцовых фрез, фасонных резцов и других углы в главной секущей плоскости не задаются, а указываются углы в других секущих плоскостях, удобных для изготовления инструмента. Эти углы необходимо задать такими, чтобы передний, задний углы и угол наклона режущей кромки, характеризующие процесс резания, были оптимальными. Для проектирования и изготовления инструмента необходимо знать зависимости между углами, измеряемыми в различных плоскостях.
Для вывода искомых зависимостей через произвольную т.О (см. рис.3.12) проведем единчные векторы на передней поверхности резца: D - в главной секущей плоскости, B - по линии, касательной к режущей кромке, С - в произвольном направлении. Поскольку векторы D, B, С лежат в одной плоскости, то их векторно-скалярное произведение равно нулю. Векторы D, В, С определяются их проекциями на координатные оси Ox, Oy, Oz:
D = j cosγ + k sinγ, B = i cosλ – k sinλ,
C = i cosγi cosΨ + j cosγi sinΨ + k sinγi
Поскольку векторно сколярное произведение ВСD = 0, то определитель
0 |
сosγ |
sinγ |
= 0 |
сosλ |
0 |
– sin λ |
|
cosγi cosΨ |
cosγi sinΨ |
sinγi |
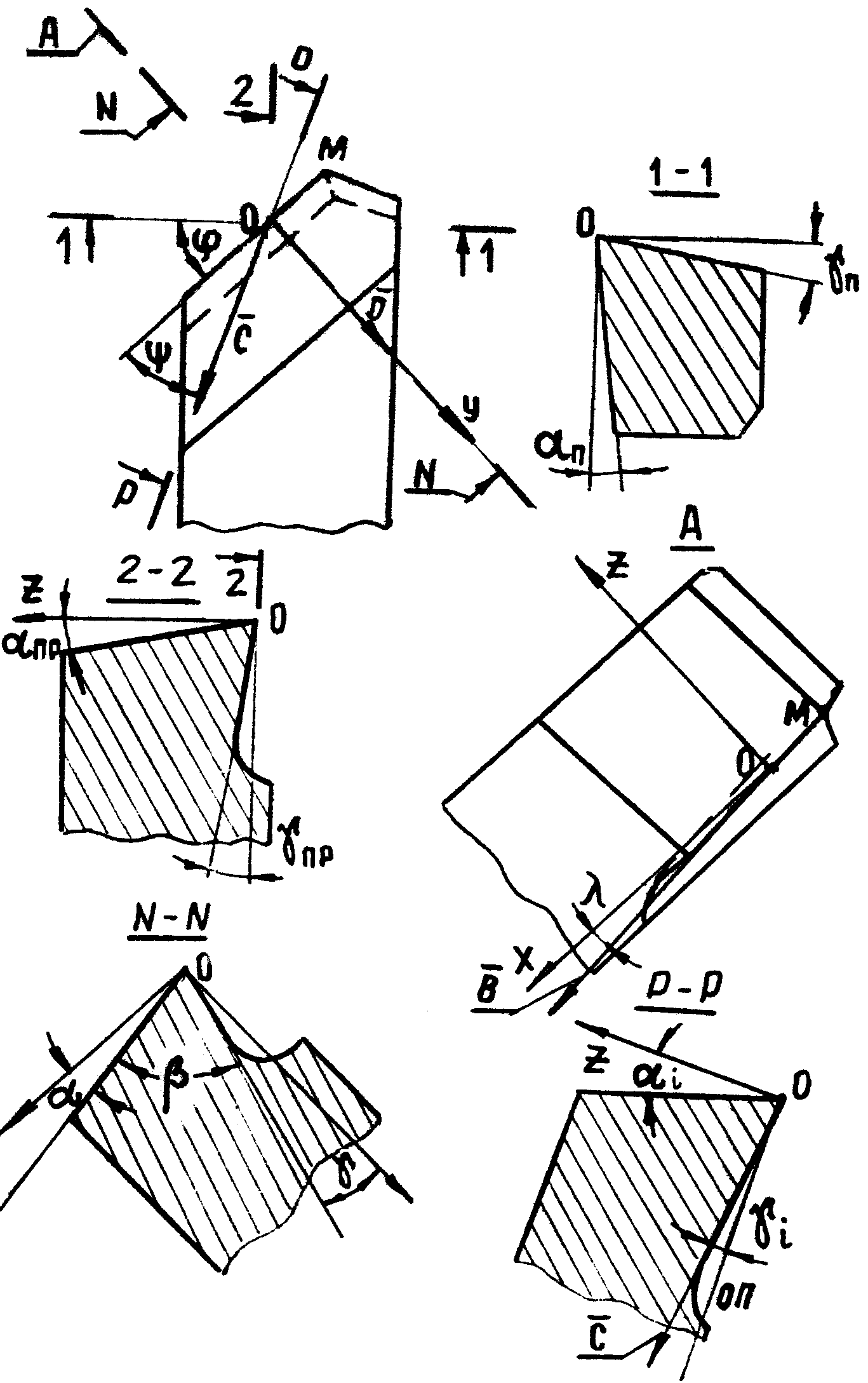
Рис. 3.12.Углы резца в различных секущих плоскостях
Решив данное уравнение относительно tg γi, получим:
tg γi = tg γ sinΨ – tg λ cosΨ (3.1)
Из рис. 3.12 видно, что при Ψ = 90˚ - φ плоскость Р - Р совпадает с плоскостью 2 - 2. При этом γi = γпр, αi = αпр.
tg γпр = tgγ cosφ – tgλ sinφ.
Для идеального резца с углом заострения β = 0 имеем
γ = 90˚ - α, γпр = 90˚ - αпр;
ctg αпр = ctgα cosφ – tgλ sinφ (3.2)
Аналогично положив Ψ = 180˚ - φ, получим
tg γп = tgγ sinφ + tgλ cosφ; (3.3)
ctg αп = ctgα sinφ + tgλ cosφ (3.4)
Выполнив такие же операции для вспомогательной режущей кромки, получим формулы, отличающиеся тем, что буквенные обозначения углов будут иметь индекс 1. Формулы (3.1. - 3.4.) применяются при проектировании режущего инструмента.
Для некоторых инструментов: сверл, торцовых фрез и других необходимо определить углы γ, λ, и α, по углам γпр, αпр, γп, αп, и φ.
Из формул (3.1. - 3.4.) имеем
tg γ = tgγпр cosφ + tgγп sinφ;
tg λ = tgγп cosφ - tgγпр sinφ;
ctg α = ctgαпр cosφ + ctgαп sinφ.
3.7. Влияние установки резца на станке на его геометрию
3.7.1. Резец повернут в основной плоскости
Рис. 3.13. Влияние поворота резца в основной плоскости на углы в плане
|
|
Поворот резца в основной плоскости на угол Ψ (см. рис.3.13) приводит к изменению углов в плане: φд = φ ± Ψ, φ1д = φ1 ± Ψ. Он производится на практике по часовой стрелке для уменьшения угла в плане φ с целью повышения стойкости инструмента, а против часовой стрелки – для увеличения угла в плане с целью повышения точности обработки и устранения вибраций.
3.7.2. Резец смещен по вертикали от оси вращения шпинделя токарного станка
Смещение резца обусловлено его неточной установкой. Если резец смещен вверх от оси вращения на величину h (см. рис.3.14), то плоскость резания ПР и основная плоскость ОП повернуты на угол η относительно плоскостей ПР1 и ОП1, относящихся к точно установленному по вертикали резцу. При этом действительные передний γд и задний αд углы для положения 2 отличаются от углов для положения 1.
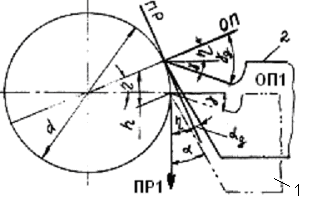
Рис. 3.14. Влияние смещения резца по высоте
относительно оси вращения шпинделя
токарного станка на геометрию
Для
случаев, когда
![]() имеем:
имеем:
γд = γ + η, αд = α – η, sin η = 2h/d.
В
общем случае, когда
![]() ,
смещение резца по вертикали вызывает
изменение переднего и заднего углов,
измеренных в продольной секущей
плоскости, на угол η.
Передний и задний углы, а также угол
наклона режущей кромки для положения
резца 1 (см. рис.3.14) будут отличаться от
углов для положения 2. Обозначим последние
индексом 2. Расчет производится в
следующей последовательности.
,
смещение резца по вертикали вызывает
изменение переднего и заднего углов,
измеренных в продольной секущей
плоскости, на угол η.
Передний и задний углы, а также угол
наклона режущей кромки для положения
резца 1 (см. рис.3.14) будут отличаться от
углов для положения 2. Обозначим последние
индексом 2. Расчет производится в
следующей последовательности.
Вначале определяют углы для положения 1:
tg γпр = tgγ cosφ – tgλ sinφ;
tg γп = tgγ sinφ + tgλ cosφ;
ctg αпр = ctgα cosφ – tgλ sinφ;
ctg αп = ctgα sinφ + tgλ cosφ.
Затем определяют эти же углы для положения 2:
η = arcsin 2h/d, γп2 = γп, αп2 = αп, γпр2 = γпр ± η;
αпр2
=
α
![]() η.
η.
Здесь верхние знаки относятся к обработке наружных поверхностей, нижние к обработке внутренних, при этом h > 0, если резец смещен вверх, и h < 0, если резец смещен вниз относительно оси вращения заготовки.
После этого определяют углы в координатных плоскостях для положения резца 2:
tg γ2 = tgγпр2 cosφ + tgγп sinφ,
ctg α2 = ctgαпр2 cosφ +ctgαп sinφ,
tg λ2 = tgγп cosφ – tgγпр2 sinφ
Как следует из формул, углы γ2, α2, λ2 изменяются тем больше, чем больше угол η. Последний увеличивается с уменьшением диаметра обрабатываемой заготовки и увеличением смещения h. Поэтому данный вопрос имеет значение для обработки деталей малого диаметра и отрезке на токарном станке. В этих случаях рекомендуется резец точно устанавливать по высоте.