Упражнения 1

1. Получить полиномы Лежандра, используя производящую функцию, для n=0,1,2.

2. Получить полиномы Лежандра, используя формулу Родрига, для n=0,1,2,3,4,5.

3. Получить полиномы Лежандра, используя рекуррентную формулу для коэффициентов, для n=0,1,2,3,4,5,6.

4. Исследовать (найти точки перегиба, максимумов и минимумов) полиномы Лежандра для n=0,1,2,3,4,5.

5. Получить присоединенные функции Лежандра для n, m=0,1,2,3,4. Выразить данные функции через тригонометрические функции.

6. Получить сферические функции и их линейные комбинации для l=0,1,2.

7. Показать, что сферические функции ортонормированны. Ограничиться l=0,1.

Глава II. Полиномы Чебышева-Эрмита и Чебышева-Лагерра

§1 Полиномы Чебышева- Эрмита

1.1. Дифференциальная формула

Полиномы Чебышева-Эрмита определим по аналогии с полиномами Лежандра при помощи производящей функции , полагая:

. (1)

Отсюда, в силу теоремы Коши, следует

, (2)

где С – замкнутый контур в плоскости комплексного переменного , охватывающий точку . Вводя новую переменную интегрирования

,

,

,

преобразуем (2) к виду

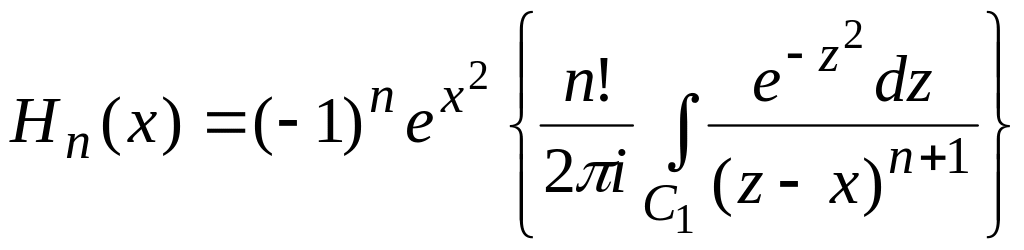, (3)

где С₁- контур, охватывающий точку . В силу теоремы Коши, выражение в фигурных скобках равно . В результате получаем из (3) дифференциальную формулу (4)

. (4)

Эта формула показывает, что есть полином степени n, причем

. (5)

1.2. Рекуррентные формулы

Дифференцируя производящую функцию

,

по и , находим

, (6)

. (6a)

В каждое из тождеств (6) подставим ряд (1) для .

,

Меняем коэффициенты

.

Собирая члены при и приравнивая их к нулю, мы сможем получить две рекуррентные формулы. Используем первую формулу из (6) и найдем

. (7)

Получим еще одну реккурентную формулу используя соотношение (6а)

,

.

Получаем рекуррентную формулу

. (8)

Формула (8) позволяет последовательно определять для всех n>1, зная , .

1.3. Уравнение Чебышева- Эрмита

Найдем уравнение, которому удовлетворяет . Используя соотношение (7) заменяем в (8) последнее слагаемое и дифференцируем:

,

,

.

Таким образом, мы получили уравнение Чебышева-Эрмита, которое можно записать в операторной форме:

. (9)

Отсюда видно, что полином Чебышева-Эрмита является собственной функцией, соответствующей собственному значению и сводится к задаче Штурма-Лиувиля:

найти те значения , при которых уравнение Чебышева- Эрмита

, , (10)

имеет нетривиальное решение, возрастающее при , не быстрее чем конечная степень .

Решение этой задачи можно было бы искать в виде степенного ряда . Подставляя этот ряд в уравнение (10), получим для коэффициентов рекуррентную формулу

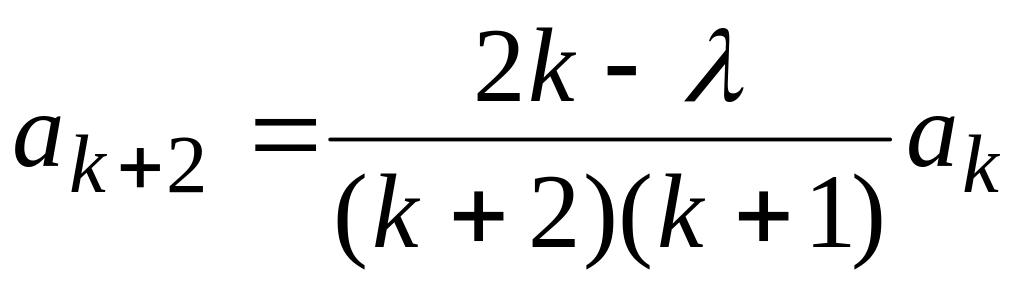. (11)

Из формулы (11) видно, что при все коэффициенты обращаются в 0 для и ряд обрывается. Только при требовании может быть выполнено условие на бесконечности. Полученные полиномы будут определены с точностью до постоянного множителя. Выбирая , получим полиномы .