§3 Сферические функции

3.1. Сферические функции

Сферические функции проще всего могут быть введены при решении уравнения Лапласа для шаровой области методом разделения переменных. Разделение переменных в уравнении Лапласа в сферических координатах:

,

,

где - угловая часть, - радиальная часть оператора Лапласа в сферических координатах.

, (1)

. (2)

Решение уравнения Лапласа для функции ищем в виде:

, (3)

,

. (4)

Для определения R(r) получаем уравнение Эйлера:

, (5)

где - константа разделения.

Для определения получаем уравнение

. (6)

Из условия ограниченности функции на сфере любого радиуса следует, что функция должна удовлетворять условиям , , а также .

Ограниченное решение уравнения (6), обладающие непрерывными производными до второго порядка, называются сферическими функциями.

Решение задачи для ищем также методом разделения переменных, полагая

. (7)

Функция удовлетворяет уравнению

.

Умножим на и поделим на (7)

,

, (8)

где m-константа разделения. Из (8) следует, что

. (9)

Задача для с условием периодичности имеет решение лишь при целом m, и линейно независимыми решениями являются функции и .

Функция определяется из уравнения и условий ограниченности при и :

, (10)

, (11)

, (12)

определенная в (12) есть решение (9).

Если потребовать выполнение условия

,

m-любое число m=0,1,-1,2,-2…

,

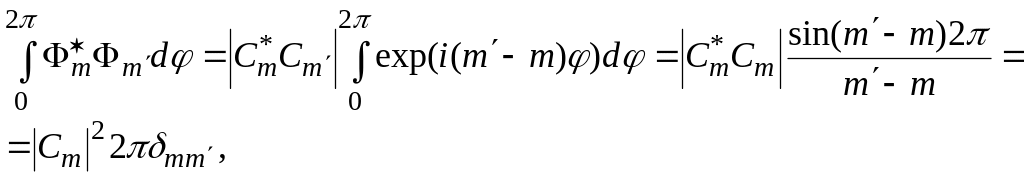
, m=0,1,-1. (14)

Выберем новую переменную и обозначая , получаем для уравнение присоединенных функций (15):

,

,

подставляем все в (10)

,

. (15)

Полученное уравнение является уравнением для присоединенных функций Лежандра

.

Потребуем, чтобы функции были нормированными

,

,

, (16)

, (17)

где , .

. (18)

Уравнение (6) имеет решение (18) при собственных значениях . Найдем несколько сферических функций

,

.

Легко проверить, что сферические функции являются ортонормированными, т.е. справедливо:

,

,

,

.

Кроме сферических функций используется понятие сферических гармоник, которые определяется следующим образом как линейная комбинация (2l+1) сферических функций:

,

Решение уравнения имеет вид:

.

Специфика заключается в нахождении радиальной части волновой функции R(r). Найдем решение уравнения Эйлера:

,

,

,

,

,

.

Тогда , есть решение для внутренней краевой задачи, а есть решение для внешней краевой задачи.

3.2. Ортогональность системы сферических функций

Докажем, что сферические функции, соответствующие различным значениям , ортогональны на поверхности сферы . Пусть и удовлетворяют уравнениям

; , (19)

где

.

Нетрудно видеть, что имеет место формула

, (20)

которая легко получается интегрированием по частям ( ). На поверхности сферы:

,

.

Так что используя

и формулу (20) можно записать в виде

.

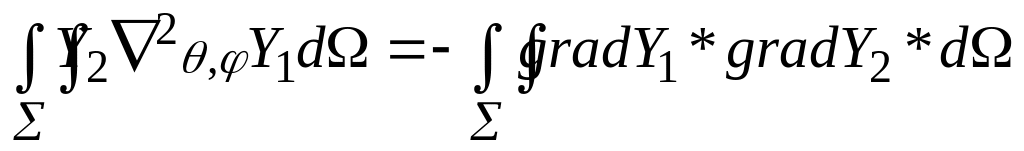Меняя местами в формуле (20) функции и , а также вычитая полученную формулу из формулы (20), будем иметь:

. (21)

Формулы (20) и (21) являются формулами Грина для операторов сферических функций.

Из формулы (21) легко следует ортогональность и . В самом деле, пользуясь уравнениями (19), получим из формулы (21)

,

откуда при получим, что

,

или

.

Тем самым доказана ортогональность сферических функций, соответствующих разным .