§1 Полиномы Лежандра

1.1. Производящая функция и полиномы Лежандра

Полиномы Лежандра тесно связаны с фундаментальным решением уравнения Лапласа 1/R, где R – расстояние от точки М до фиксированной точки М₀. Пусть r и r₀ – радиусы-векторы точек М и М₀, а - угол между ними. Очевидно, можно записать

, (1)

где ,

,

при , , .

,

при , , .

Функция

,

называется производящей функцией полиномов Лежандра.

Разложим функцию в ряд по степеням :

, , . (2)

Коэффициенты в разложение (2) являются полиномами n-й степени и называются полиномами Лежандра.

В силу теоремы Коши из формулы (2) следует, что

. (3)

Перейдем в комплексную плоскость ( , ). Используя интегральную формулу Коши и пользуясь формулой для производной

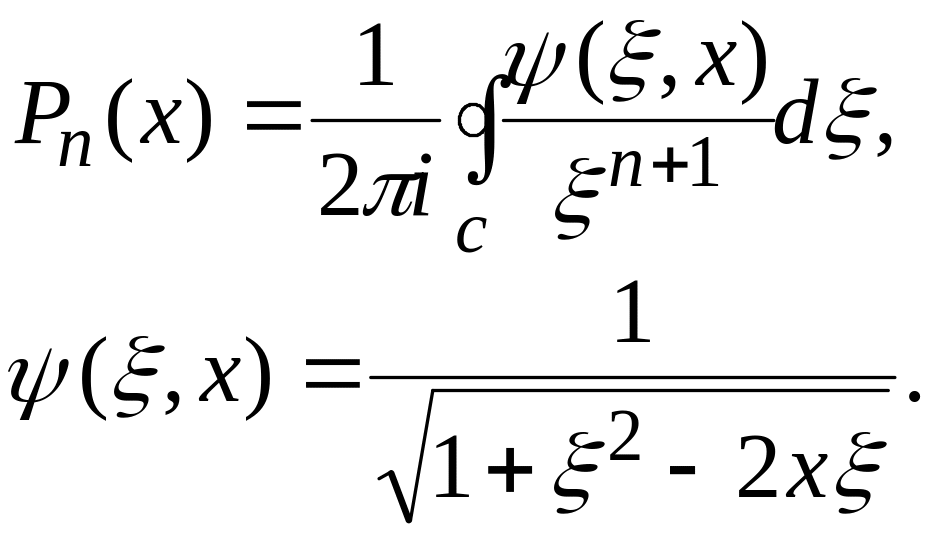(4)

Полагая , находим , ,

, (5)

где С₁- любой контур, окружающий точку x=z. Подинтегральная функция имеет особенность, а именно полюс (n+1) порядка.

С помощью теории вычетов получим:

. (6)

Из формулы (6) непосредственно видно что:

1. P_n(x) есть полином степени n;

2. Полином P_n(x) содержит степени x той же четности, что и номер n, так что

. (7)

Граничное условие в точке x=1, дает:

,

т.е. .

Формула (6) называется дифференциальной формулой для полиномов Лежандра или формулой Родрига. С учетом (7)

.

Отметим, что из (1) и (3) следует разложение потенциала

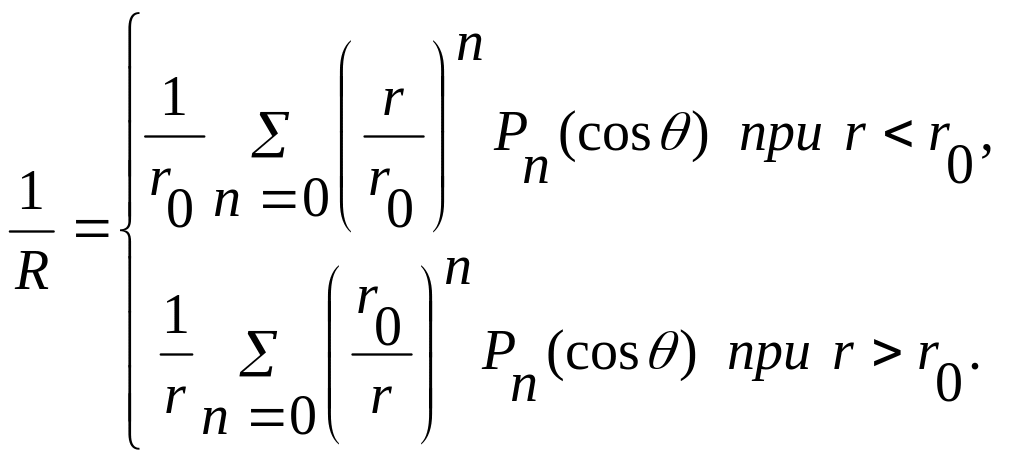(8)

1.2. Рекуррентные формулы

Используем производящую функцию

,

и найдем частные производные по и по , чтобы получить два уравнения:

,

, (9)

,

. (10)

Запишем левую часть формулы (9) в виде степенного ряда относительно , подставив в нее ряд (3) для и ряд . Коэффициент при ρⁿ полученного ряда , в силу (9), равен нулю при всех x. Рассмотрим эту процедуру подробнее. Возьмем производную по и подставим в формулу (9):

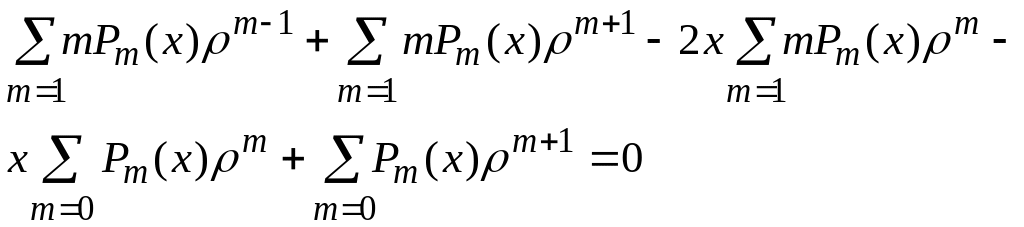
Сделаем замены индексов, чтобы "собрать" слагаемые с одинаковыми степенями

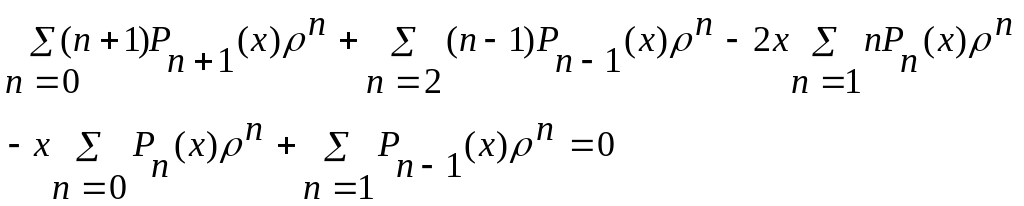
Запишем коэффициенты при ⁰, ¹,…, ⁿ.

, где n ≥2. (11)

Таким образом, выражение (11) представляет собой общее рекуррентное соотношение. Домножим (9) на , (10) на ( ) и вычтем одно из другого

, (12)

,

используя процедуру примененную ранее получим соотношение

, (13)

или рекуррентную формулу

. (14)

Продифференцируем по x соотношение (11) и исключая и заменяя n+1 на n получим новую рекуррентную формулу:

. (15)

1.3. Уравнение Лежандра

Найдем дифференциальное уравнение, решением которого является . Для этого исключим P_n-1(x) и из (14) и (15). Подставляем (14) в (15):

.

Продифференцируем полученное соотношение по x и еще раз применим формулу (14) для :

.

В результате приходим к уравнению

. (16)

Соотношение (16) представляет собой уравнения Лежандра. Тем самым доказано, что полиномы Лежандра являются собственными функциями, соответствующими собственным значениям , следующей задачи:

найти такие значения λ, для которых на отрезке существуют нетривиальное решение уравнение Лежандра

, (17)

с областью с условием ограниченности при и удовлетворяющие условию нормировки . Таким образом, нетривиальное решение существует при

.