14. Последовательные этапы построения модели множественной регрессии.

Начальными этапами являются выбор одной из наиболее существенных независ переменных и выбор формы уравнения регрессии. В общем виде: y=f(x1,x2…xn). Для отбора независ переменных проводится предварительный теоретич анализ, а затем количественное измерение тесноты связи у с отобранными ф-рами. Теоретический анализ базируется на экспертных оценках значимости важнейших условий и предпосылок, которыми определяют состояние зависимой переменной. На этапе количественного анализа из предварительно отобранных ф-в необходимо отобрать наиболее значимые и проверить их на мультиколлениарность(связь независимых ф-в м/у собой). Если м/у некоторыми ф-рами пресутствует достаточно тесная связь, то будут искажены результаты оценки связи этих ф-в с у. Общие требования: 1. Д.б. существенные ф-ры реально влияющие на у. 2. Ф-ры д.б. количественно измеряемы, если прямой колич меры нет, то необходимо попытаться дать им бальную оценку. 3. Ф-ры не д.б. зависимы друг от друга, проверка на мультиколлениарность. Отбор ф-в можно выполнить используя таблицу парных коэф корреляции или применить спец. мат. приемы: 1. Отсев ф-в. 2. Добавление ф-в. 3. Пошаговое

16. Выбор формы уравнения множественной регрессии.

Наиболее растпространенным элементом является линейный модуль: y=a+b1x1+b2x2+b3x3+E. Среди нелинейных модулей: 1. Гипербола y= 1/ (a+b1x1+b2x2) 2степенная y=a+x1^b1*x2^b2. Различие линейной и нелинейной модели в том, что в нелин модели трудней интерпретировать параметры. В лин модели коэф регрессии b имеет очевидный экономический смысл и показывает на сколько измеряется у при изменении х, при условии предположения, что влияние всех остальных ф-в сохраняется неизменным. В нелинейной модели b инетрпретируется в относит величинах и такая интерпретация менее очевидна. Расчет параметров нелин модели можно выполнять либо ручным способом используя логарифмирование, либо на калькуляторе. Чем больше переменных в моделе тем строже требования к числу наблюдений.

17. Натуральная и стандартизованная формы модели множественной регрессии.

y=a+b1x1+b2x2 – естественная(натуральная) форма.

Чтобы обеспечить сопоставимость характеристик силы связи при множествен регрессии необходимо от абсолютной формы перейти к их относительной форме.

t_y= β₁t_x1+ β₂t_x2 – стандартизованная модель

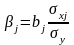
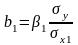
Для расчета β-коэф необходимо использовать информацию о парных коэф корреляции в зависимости от числа независ переменных в модели, ф-лы расчета β-коэф имеют вид:

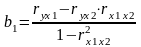
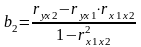
Определить силу связи м/у ф-ром х и следствием у в относит форме и благодаря этому есть возможность оценить какой ф-р и во сколько раз сильнее влияет на следствие у.

19. Показатели силы связи во множественной регрессии в абсолютной и относительной форме.

Для обеспечения сопоставимости характеристик силы связи для лин моделей используется замена натуральной формы уравнения на стандартизованную. При этом коэф регрессии b заменяется на β-коэф, кот имеет относительную форму. Для лин моделей в кач-ве относит характеристики силы связи применяются коэф эластичности:

(δ) линейная модель (%) – для лин и нелин моделей.

b_i- на какую величину изменится у, при увелич х на 1 ед. β_i – коэф дают оценку влияния ф-ра x в относительной форме и определяют на сколько своих средних квадратичных отклонений (δ_у) в среднем изменяется зависимая переменная у при изменении переменной х на одно свое среднеквадратичное отклонение при фиксированных значениях других переменных, включенных в данную модель регрессии. 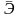(относительная оценка силы связи) показывает на сколько % в среднем изменится зависимая переменная у при изменении переменной на 1%, если другие независимые переменные считать неизменными. Коэф эластичности – универсальный инструмент и м.б. использован при анализе как множественных так и парных связей.

20. коэф множественной корреляции и коэф множественной детерминации. Сущ несколько способов оценки тесноты связи: R – коэф множественной корреляции, R²скорректир – скорректированный коэф множественной детерминации, R² – множественный коэф детерминации.

Р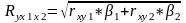 асчет линейного коэф множественной корреляции с использованием коэф r_yxi и β_i:

коэф множественной детерминации на основе парных коэф корреляции:

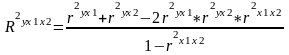
где парные коэф корреляции высчитываются по ф-лам: 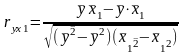и т.п.

Интерпретация R: дается в мерах тесноты связи путем оценки степени близости показателя к единице. Меньше 0,3 – лабая теснота связи, больше 0,3 – умеренная теснота связи.

R²скорректир. Для одного и того же числа наблюдений n, коэф детерминации принимает разные значения в зависимости от числа переменных в модели и степени нелинейности связи.

Коэф скорректированный на число степеней свободы:

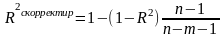
скорректированный коэф множественной детерминации не имеет самостоятельного эластичного значения, используется только для сравнения с обычным коэф детерминации. Модель считается хорошей, если невелика разница м/у обычным и скорректированным коэф детерминации, а сама величина этих коэф близка к 1.