Побудова економіко-математичної моделі.

Позначимо через хj кількість j-го компонента в суміші (т), j = 1,2,3,4.

Перше обмеження забезпечує потрібне значення октанового числа в суміші:

.

Вміст сірки в суміші має не перевищувати 0,3 %:

,

а загальна маса утвореної суміші має дорівнювати 1000 т:

.

Використання кожного компонента має не перевищувати його наявного обсягу:

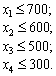
Собівартість суміші визначається за формулою:

.

Загалом, економіко-математична модель задачі має вигляд:

за умов:

.

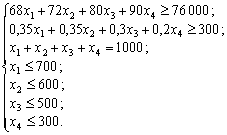
Розв’язавши цю задачу симплексним методом отримуємо оптимальний план: х1=0, х2=500, х3=500, х4=0. Цільова функція дорівнює:

min F = 40*0+45*500+60*500+90*0 = 52500 (грош. од.)

Отже, для того, щоб отримати 1000 т бензину А-76 з мінімальною собівартістю у 52500 грош. од. потрібно використати 500 тонн 2 компоненту та 500 тонн третього компоненту.

2. Симплексним методом знайти розв’язок задачі лінійного програмування

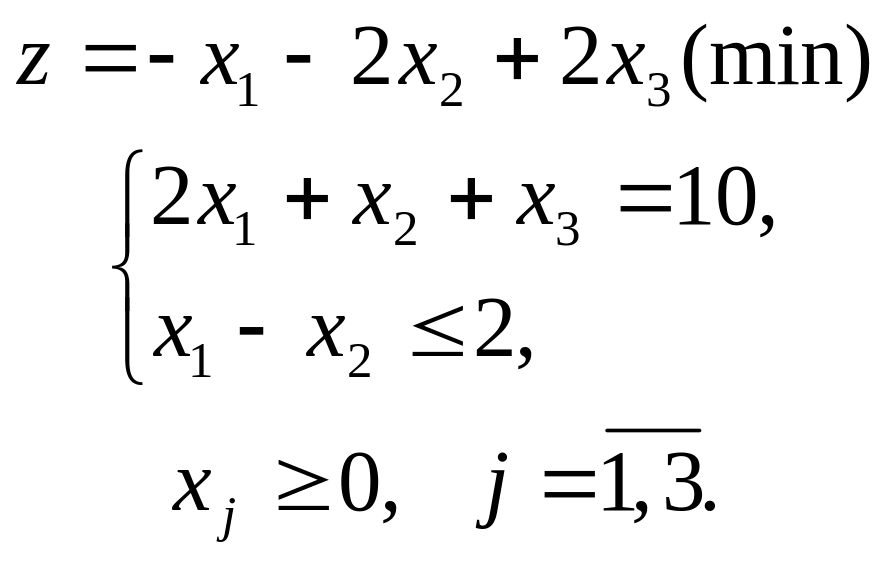
Розв’язання

Застосуємо алгоритм симплекс-методу:

1. min Z = – x₁ -2x₂ + 2x₃ + 0x₄;

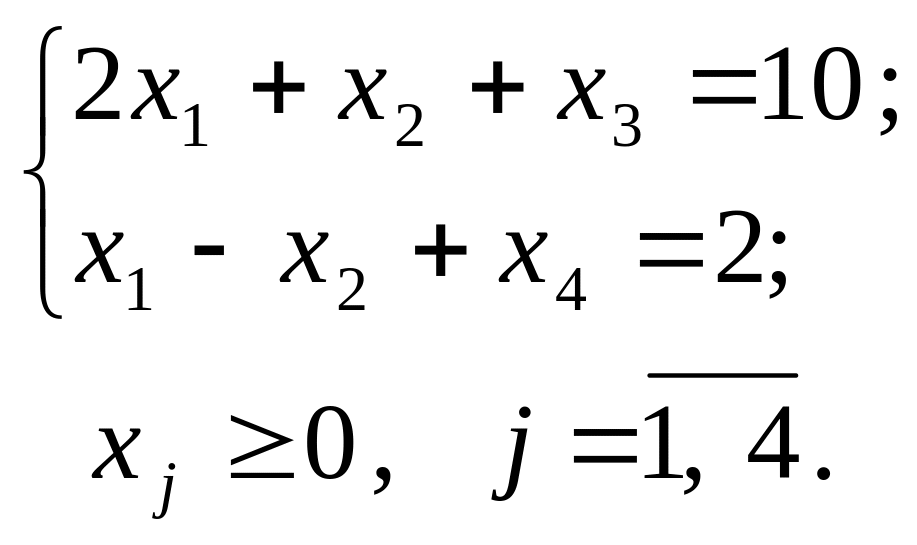
2. Векторна форма запису системи обмежень має вигляд:

,

де , , , , .

У цій задачі х₃ та х₄ — базисні змінні, а х₁, х₂ — вільні. Нехай х₁ = х₂ = 0, тоді х₃ = 10; х₄ = 2.

Перший опорний план задачі:

X₀ = (0; 0; 10; 2), Z₀ = 20.

_{4. Подальше розв’язування прямої задачі подано у вигляді симплексної таблиці:}

Базис	Сбаз		План	-1	-2	2	0	
				х1	х2	х3	х4
х3	2		10	2	1	1	0	5
х4	0		2	1	-1	0	1	2
Zj – сj  0			20	5	4	0	0
х3	2		6	0	3	1	-2	2
х1	-1		2	1	-1	0	1	-2
Zj – сj  0			10	0	9	0	-5
х2		-2	2	0	1	0,33	-0,67	-3
х1		-1	4	1	0	0,33	0,33	12
Zj – сj  0			-8	0	0	-3	1
х2		-2	10	2	1	1	0
х4		0	12	3	0	1	1
Zj – сj  0			-20	-3	0	-4	0

Оскільки всі , то з останньої симплекс-таблиці оптимальним планом задачі є вектор:

Х^* = (0; 10; 0; 12; 0),

Б ілет №21

1. Учасник експедиції складає рюкзак, і йому необхідно розв’язати питання про те, які взяти продукти. У розпорядженні є м’ясо, борошно, сухе молоко, цукор. У рюкзаку залишилось для продуктів лише 45 дм3 об’єму, до того ж необхідно, щоб загальна маса продуктів не перевищувала 35 кг. Лікар експедиції рекомендував, щоб м’яса (за масою) було більше, ніж борошна принаймні удвічі, борошна не менше, ніж молока, а молока хоча б у вісім разів більше, ніж цукру. Скільки і яких продуктів потрібно покласти в рюкзак, щоб сумарна калорійність продуктів була найбільшою? Характеристики продуктів наведені в табл. 1.

Таблиця 1 – Характеристики продуктів

Показники	Продукт
	м’ясо	борошно	молоко	цукор
Об’єм (дм3/кг)	1	1,5	2	1
Калорійність (ккал/кг)	1500	5000	5000	4000

Побудувати економіко-математичну модель задачі.