Обоснование эффективности оптимального плана. ( рентабельность)

При подстановке оптимальных двойственных оценок в систему ограничений двойственной задачи получим:

4*5³/₄ + 3*0 + 1*1¹/₄ = 24¹/₄ > 10

2*5³/₄ + 1*0 + 2*1¹/₄ = 14 = 14

1*5³/₄ + 3*0 + 5*1¹/₄ = 12 = 12

1-ое ограничение выполняется как строгое неравенство, т.е. ресурс 1-го вида использовать экономически не выгодно. И действительно в оптимальном плане прямой задачи x₁ = 0.

Поскольку теневая (альтернативная) цена больше рыночной цены этого продукта, то выгоднее продать ресурсы по рыночным ценам.

При этом разница между ценами (24¹/₄ - 10 = 14¹/₄) показывает величину изменения целевой функции F(x) при введении дополнительной единицы x_i.

2-ое ограничение двойственной задачи выполняется как равенство. Это означает, что 2-ый ресурс экономически выгодно использовать, а его использование предусмотрено оптимальным планом прямой задачи (x₂>0).

3-ое ограничение двойственной задачи выполняется как равенство. Это означает, что 3-ый ресурс экономически выгодно использовать, а его использование предусмотрено оптимальным планом прямой задачи (x₃>0).

БИЛЕТ№7

ЗАДАЧА №1

ЗАДАЧА №2

Визначити точку та характер умовного екстремуму функції за методом множників Лагранжа.

,

.

Z = 2x1^2 -4x1 +2 + 3x2^2 -18x2 + 27

Запишемо функцію Лаграyжа:

Візьмемо частинні похідні і прирівняємо їх до нуля:

З цієї системи рівнянь визначаємо координати сідлових точок.

Тобто отримали сідловy точкy:

Перевіримо за допомогою достатньої умови існування екстремуму сідлову точку .

Матриця Гессе має такий вигляд:

= - ( 0 + 0 + 0 - 4 – 0 – 6) = 10

10 > 0 => Сідлова точка, точка min

БИЛЕТ№8

ЗАДАЧА №1

ЗАДАЧА №2

Визначити точку та характер умовного екстремуму функції за методом множників Лагранжа.

,

Запишемо функцію Лаграyжа:

Візьмемо частинні похідні і прирівняємо їх до нуля:

З цієї системи рівнянь визначаємо координати сідлових точок.

Тобто отримали сідловy точкy:

Перевіримо за допомогою достатньої умови існування екстремуму сідлову точку .

Матриця Гессе має такий вигляд:

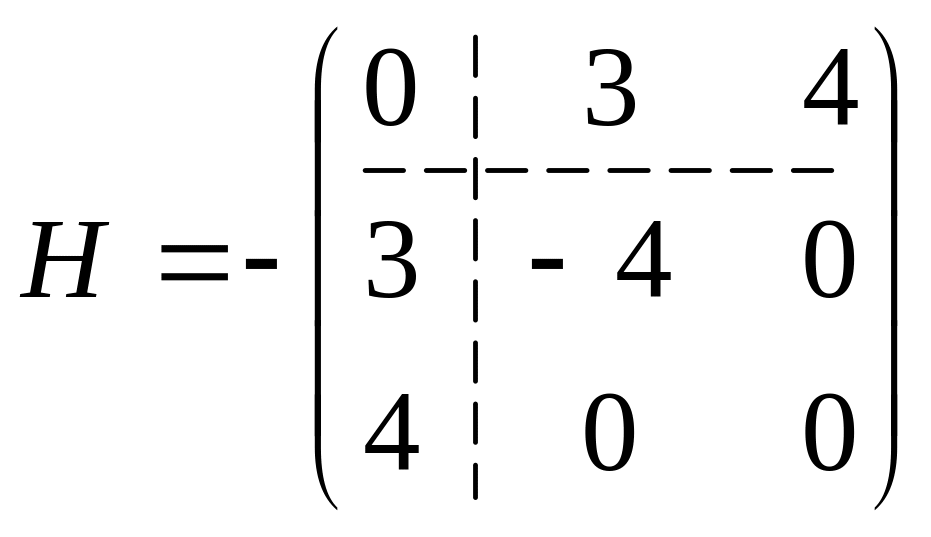
= - ( 0 +0+0+64-0 – 0 ) = -64

-64 < 0 => Сідлова точка, точка max

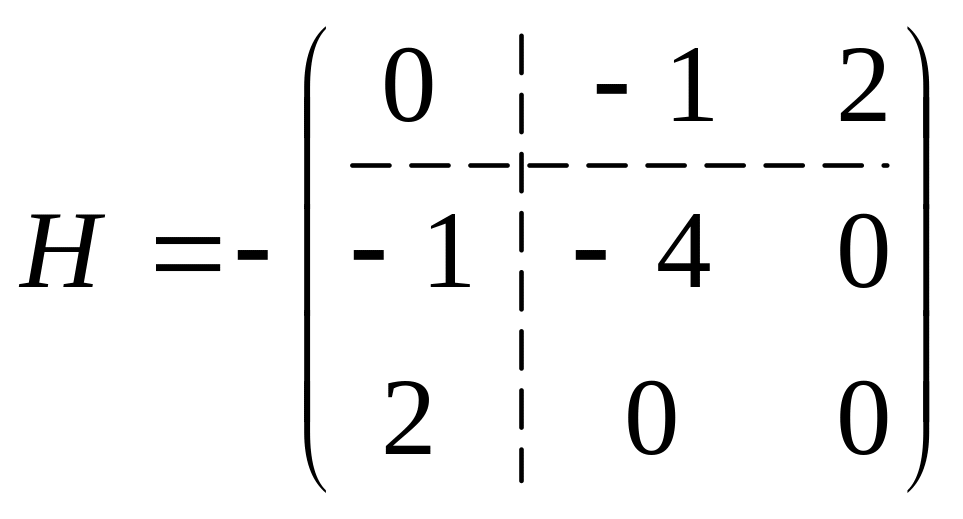
= - ( 0 +0+0+16-0 – 0 ) = -16

-16 < 0 => Сідлова точка, точка max

Ответ: Сідлова точка , точка max

БИЛЕТ№9

ЗАДАЧА №1

Сільськогосподарське підприємство задумало створити сушильний цех на виробничій площі 190м², маючи для цього 100 тис.грн. і можливість придбати устаткування двох типів А і В. Техніко-економічну інформацію про ці два види устаткування подано в таблиці:

Техніко-економічний показник	Устаткування		Ресурс
	А	В
Вартість, тис. грн.	25	10	100
Необхідна виробнича площа, м2	40	20	190
Потужність, тис. грн./рік	350	150	

Розв'язування. Нехай і — кількість комплектів устатку вання відповідно типу А і В.

Запишемо економіко-математичну модель:

і  цілі.

Розв'язуємо задачу, нехтуючи умовою цілочисловості. Остання симплексна таблиця набере вигляду:

		План	350	150	0	0
	350	1	1	0
	150		0	1
		1475	0	0	10

Значення другої змінної є дробовим числом, що не задовольняє початкові умови задачі. Побудуємо для другого рядка наведеної симплексної таблиці додаткове обмеження виду

Оскільки то додаткове обмеження набирає вигляду

Зведемо його до канонічної форми та введемо штучну змінну:

Приєднавши здобуте обмеження до останньої симплексної таблиці з умовно-оптимальним планом, дістанемо:

		План	350	150	0	0	0	М
	350	1	1	0			0	0
	150		0	1			0	0
	М		0	0			1	1
		1475	0	0	10		0	0
		М	0	0	М	М	М	0

Розв'язуючи наведену задачу, остаточно знаходимо цілочисловий оптимальний план:

.

ЗАДАЧА №2

Визначити точку та характер умовного екстремуму функції за методом множників Лагранжа.

,

.

Запишемо функцію Лаграyжа:

Візьмемо частинні похідні і прирівняємо їх до нуля:

З цієї системи рівнянь визначаємо координати сідлових точок.

Тобто отримали сідловy точкy:

Перевіримо за допомогою достатньої умови існування екстремуму сідлову точку .

Матриця Гессе має такий вигляд:

= - ( 0 + 0 + 0 - 36 – 0 – 8) = 44

44 > 0 => Сідлова точка, точка min

БИЛЕТ№10

ЗАДАЧА №1

Ф ермеру для удобрення земельної ділянки необхідно придбати 107 кг добрив. Він може купити добрива в упаковках по 35 кг вартістю 14 ум. од. або по 24 кг вартістю 12 ум. од. Метою фермера є закупівля не менше, ніж 107 кг добрив з мінімальними витратами. Причому потрібно купувати або цілу упаковку, або не купувати її зовсім, бо частину упаковки придбати неможливо.

Розв’язання. Позначимо кількість упаковок вагою 35 кг та вагою 24 кг відповідно змінними та . Маємо модель цієї задачі:

;

, — цілі числа.

У результаті розв’язування задачі будь-яким з вищенаведених методів отримаємо оптимальний план: , . Отже, за оптимальним планом найменші витрати, що дорівнюють 50 ум. од., можливі у разі закупівлі однієї упаковки добрив вагою 35 кг та трьох вагою по 24 кг.

ЗАДАЧА №2

До заданоїзадачілінійногопрограмуваннязаписатидвоїсту задачу. Розв’язавшидвоїсту задачу графічно, визначитиоптимальний план прямоїзадачі.

minZ = x1 + 2x2 + 2x3;

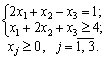
Розв’язання. За відповідними правилами побудуємодвоїсту задачу:

mахF = y1 + 4y2;

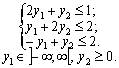
Зауважимо, щозадачінесиметричні, і тому змінна у1, щовідповідаєпершомурівнянню в системіобмеженьпрямоїзадачі, можемати будь-який знак, а змінна у2 — лишеневід’ємна.

Двоїста задача маєдвізмінні, а отже, їїможнарозв’язатиграфічно (рис. 3.2).

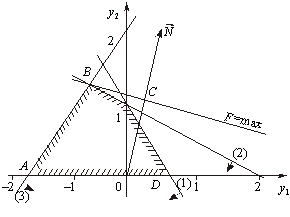
Рис. 3.2

НайбільшогозначенняцільовафункціядвоїстоїзадачіFдосягає в точціВбагатокутникаABCD. Їїкоординативизначиморозв’язаннямсистемирівнянь:

Отже, Y* = (– 2/3; 4/3); mахF = 1 х (– 2/3) + 4 х 4/3 = 14/3.

Оптимальний план прямоїзадачівизначимо за допомогоюспіввідношеньдругоїтеоремидвоїстості.

ПідставимоY* у систему обмеженьдвоїстоїзадачі і з’ясуємо, як виконуютьсяобмеженняцієїзадачі:

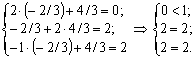
Оскільки перше обмеження для оптимального плану двоїстоїзадачівиконується як строга нерівність, то висновуємо, що перша зміннапрямоїзадачідорівнюватиме нулю х1 = 0 (перша частинадругоїтеоремидвоїстості).

Теперпроаналізуємооптимальний план двоїстоїзадачі. Оскільки друга компонента плану у2 = 4/3 додатна, то друге обмеженняпрямоїзадачі для Х*виконуватиметься як строгерівняння (друга частинадругоїтеоремидвоїстості).

Об’єднуючиздобутуінформацію, можназаписати систему обмеженьпрямоїзадачі як систему двохрівнянь, в якійх1 = 0, та визначитирештузмінних:

тобтоХ* = (0; 5/3; 2/3), minZ = 1 х 0 + 2 х 5/3 + 2 х 2/3 = 14/3.

УмоваminZ = maxF = 14/3 виконується, і тому Х* = (0; 5/3; 2/3); Y* = (– 2/3; 4/3) є оптимальними планами відповіднопрямої та двоїстої задач.

БИЛЕТ№11

ЗАДАЧА №1

На основі умовно-оптимального плану цілочисельної задачі побудувати допоміжне обмеження Гоморі, приєднати його до умовно-оптимального плану, показаного у наведений нижче таблиці, і знайти цілі значення змінних задачі лінійного програмування

І	Базис	Сб	А0	1	-1	3	4	2
				А1	А2	А3	А4	А5
1	Х1	1	14/3	1	-2/3	0	5/3	1/3
2	Х3	3	11/3	0	1/3	1	7/3	1
			47/3	0	4/3	0	14/3	11/3

Значення першої та третьої змінних є дробовими числами, що не задовольняє початкові умови задачі. Побудуємо для першого рядка наведеної симплексної таблиці додаткове обмеження виду :

.

Оскільки , , , і ,то додаткове обмеження набуває вигляду:

.

І	Базис	Сб	А0	1	-1	3	4	2	0
				А1	А2	А3	А4	А5	А6
1	Х1	1	14/3	1	-2/3	0	5/3	1/3	0	14/5
2	Х3	3	11/3	0	1/3	1	7/3	1	0	11/7
3	Х6	0	2/3	0	1/3	0	2/3	1/3	1	2
			47/3	0	4/3	0	14/3	11/3	0
			0	-	4	-	7	11	-

І	Базис	Сб	А0	1	-1	3	4	2	0
				А1	А2	А3	А4	А5	А6
1	Х1	1	6	1	0	0	3	1	2
2	Х3	3	3	0	0	0	5/3	1/3	-1
3	Х2	-1	2	0	1	0	2	1	3
			-8	0	0	0	2	7/3	-4

Розв’язавши наведену задачу, знаходимо цілочисловий оптимальний план:

ЗАДАЧА №2

Побудувати двоїсту задачу до заданої задачі лінійного програмування.

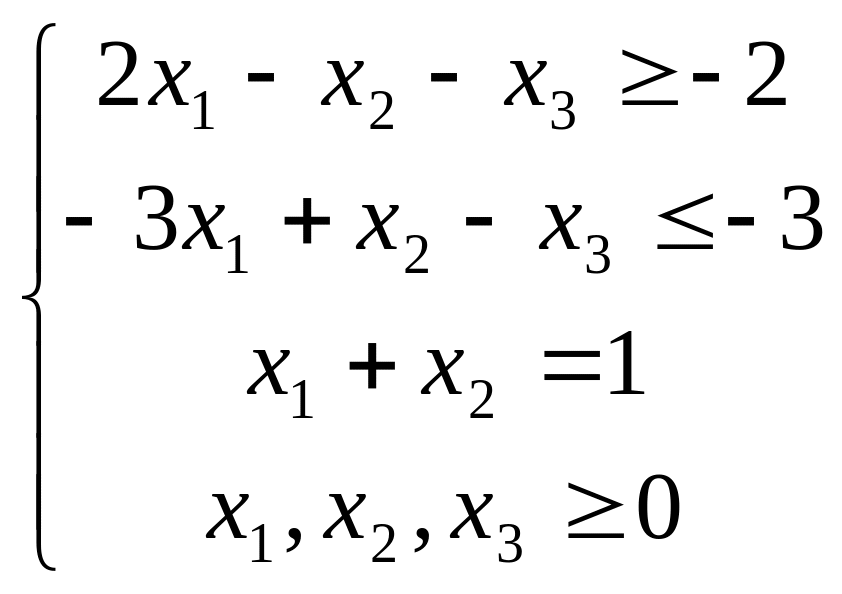
Розв’язання. Пряму задачу зведемо до стандартного вигляду. Оскільки цільова функція Z максимізується і в системі обмежень є нерівності, то вони мають бути виду « ». Тому перше обмеження задачі необхідно помножити на (–1). При цьому знак нерівності зміниться на протилежний. Отримаємо:

Двоїста задача:

Оскільки третє обмеження початкової задачі є рівнянням, то відповідна йому змінна двоїстої задачі може набувати як додатного, так і від’ємного значення.

БИЛЕТ№12

ЗАДАЧА №1

На основі умовно-оптимального плану цілочисельної задачі побудувати допоміжне обмеження Гоморі, приєднати його до умовно-оптимального плану, показаного у наведений нижче таблиці, і знайти цілі значення змінних задачі лінійного програмування

І	Базис	Сб	А0	-4	1	2	0	3
				А1	А2	А3	А4	А5
1	Х1	-4	7/2	1	-5/2	0	5/2	-3/2
2	Х3	2	5/2	0	1/2	1	31/2	11/2
			-9	0	10	0	21	14

Значення першої та третьої змінних є дробовими числами, що не задовольняє початкові умови задачі. Побудуємо для першого рядка наведеної симплексної таблиці додаткове обмеження виду :

Наприклад, для , ;

для , .

.

Оскільки , , , і ,то додаткове обмеження набуває вигляду:

.

І	Базис	Сб	А0	-4	1	2	0	3	0
				А1	А2	А3	А4	А5	А6
1	Х1	-4	7/2	1	-5/2	0	5/2	-3/2	0
2	Х3	2	5/2	0	1/2	1	31/2	11/2	0
3	Х6	0	1/2	0	1/2	0	1/2	1/2	1
			-9	0	10	0	21	14	0
			0	-	5	-	10,5	7	-

І	Базис	Сб	А0	1	-1	3	4	2	0
				А1	А2	А3	А4	А5	А6
1	Х1	-4	6	1	0	0	5	1	5
2	Х3	2	2	0	0	1	15	5	-1
3	Х2	1	1	0	1	0	1	1	1
			-19	0	0	0	11	4	-5

Розв’язавши наведену задачу, знаходимо цілочисловий оптимальний план:

ЗАДАЧА №2

Побудувати двоїсту задачу до заданої задачі лінійного програмування.

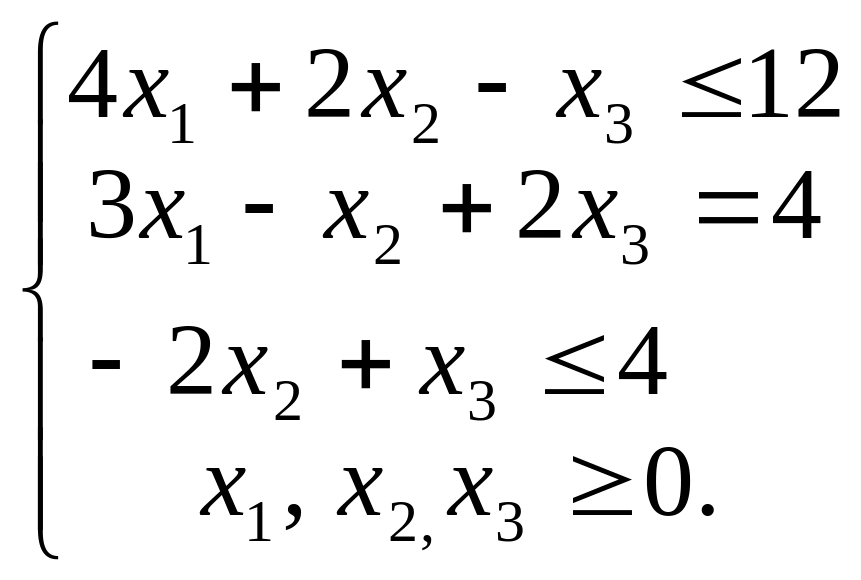
Розв’язання. Пряму задачу зведемо до стандартного вигляду. Оскільки цільова функція Z максимізується і в системі обмежень є нерівності, то вони мають бути виду « ».

Двоїста задача:

Оскільки третє обмеження початкової задачі є рівнянням, то відповідна йому змінна двоїстої задачі може набувати як додатного, так і від’ємного значення.

БИЛЕТ №14

Задача 1

Фірма має 1 млн грн обігових коштів. Відомі вит­рати грошей у кожному місяці, а також обов’яз­кові залишки обігових коштів на кінець кожного місяця. Також передбачається, що для успішного функціонування фірма витрачатиме значно меншу суму, ніж 1 млн грн. Отже, решту коштів можна надавати у кредит. Необхідно визначити оптимальний розподіл обігових коштів протягом кварталу для досягнення максимального прибутку за процентними ставками, якщо відомі витрати та потреби в резервах:

1.01 —31.01: витрати — 80 000 грн; необхідний запас на 31.01 — 300 000 грн;

1.02 —28.02: витрати — 30 000 грн; необхідний запас на 28.02 — 200 000 грн;

1.03 —31.03: витрати — 50 000 грн; необхідний запас на 31.03 — 190 000 грн.

Кредит терміном на 1 місяць дає 2 % прибутку, терміном на 2 місяці — 5 %, а терміном на 3 місяці — 8 %.

Вважатимемо, що кредити надаються першого числа кожного місяця і погашаються також першого числа відповідного місяця.

Побудова економіко-математичної моделі.

Кредити терміном на один місяць можна надавати кожного місяця протягом кварталу, тому позначимо через х₁₁ суму кредиту, що надано на один місяць з 1.01, аналогічно х₁₂,х₁₃ — суми одномісячних кредитів, що надані відповідно в другому та у третьому місяцях.

Кредити терміном на два місяці протягом першого кварталу можна надавати лише в першому і другому місяцях, тому позначимо через х₂₁ суму кредиту, що надано на два місяці в січні, х₂₂ — суму кредиту, що надана в лютому на два місяці. Нарешті, кредит на три місяці можна надати лише один раз із 1.01, його позначимо через х₃₁.

Розглянемо ситуацію на початку першого місяця кварталу: початкова сума 1 млн грн витрачатиметься на вкладення коштів у всі види кредитів, потреби в обігових коштах для господарської діяльності фірми становитимуть 80 000 грн, а на кінець місяця фірма бажає мати резерв обсягом 300 000 грн. Отже, використання коштів у січні можна описати у моделі так:

.

Наявні кошти в кінці місяця (окрім резерву) визначаються за формулою:

На початку другого місяця сума S1 може надаватися в кредит, але лише двох видів та має забезпечувати витрати діяльності. Одночасно на початку другого місяця повертаються кошти, що є процентами за одномісячний кредит, який було надано в січні. Враховуючи необхідність резерву на кінець другого місяця, маємо таке обмеження щодо використання коштів у лютому:

,

а наприкінці лютого обсяг наявних коштів становитиме:

.

Аналогічно запишемо використання коштів у березні:

.

Загальна сума коштів, отриманих як проценти за надані кредити, дорівнюватиме:

.

Загалом математична модель цієї задачі має вигляд:

за умов:

Задача 2

F(X) = x₁ - 3x₂ + x₃

x₁ + 2x₂ - x₃≥2

2x₂ + 4x₃≤7

Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).

В 1-м неравенстве смысла (≥) вводим базисную переменную x₄ со знаком минус. В 2-м неравенстве смысла (≤) вводим базисную переменную x₅.

1x₁ + 2x₂-1x₃-1x₄ + 0x₅ = 2

0x₁ + 2x₂ + 4x₃ + 0x₄ + 1x₅ = 7

Введем искусственные переменные x: в 1-м равенстве вводим переменную x₆;

1x₁ + 2x₂-1x₃-1x₄ + 0x₅ + 1x₆ = 2

0x₁ + 2x₂ + 4x₃ + 0x₄ + 1x₅ + 0x₆ = 7

Для постановки задачи на минимум целевую функцию запишем так:

F(X) = x₁-3x₂+x₃+Mx₆ → min

Разрешающий элемент равен (2) и находится на пересечении ведущего столбца и ведущей строки.

Базис	B	x1	x2	x3	x4	x5	x6	min
x6	2	1	2	-1	-1	0	1	1
x5	7	0	2	4	0	1	0	31/2
F(X1)	2M	-1+1M	3+2M	-1-1M	-1M	0	0	0

Базис	B	x1	x2	x3	x4	x5	x6	min
x2	1	1/2	1	-1/2	-1/2	0	1/2	-
x5	5	-1	0	5	1	1	-1	5
F(X2)	-3	-21/2	0	1/2	11/2	0	-11/2-1M	0

Окончательный вариант симплекс-таблицы:

Базис	B	x1	x2	x3	x4	x5	x6
x2	31/2	0	1	2	0	1/2	0
x4	5	-1	0	5	1	1	-1
F(X3)	-101/2	-1	0	-7	0	-11/2	-1M

Оптимальный план можно записать так:

x₂ = 3¹/₂

x₄ = 5

F(X) = -3•3¹/₂ = -10¹/₂

БИЛЕТ №15

Задача 1

F(X) = - x₁ - x₂ + 3x₃

x₁ - x₂ + 2x₃≤2

2x₁ + x₂ + 3x₃≤8

Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).

В 1-м неравенстве смысла (≤) вводим базисную переменную x₄. В 2-м неравенстве смысла (≤) вводим базисную переменную x₅.

1x₁-1x₂ + 2x₃ + 1x₄ + 0x₅ = 2

2x₁ + 1x₂ + 3x₃ + 0x₄ + 1x₅ = 8

Базис	B	x1	x2	x3	x4	x5
x4	2	1	-1	2	1	0
x5	8	2	1	3	0	1
F(X0)	0	1	1	-3	0	0

Базис	B	x1	x2	x3	x4	x5	min
x4	2	1	-1	2	1	0	1
x5	8	2	1	3	0	1	22/3
F(X1)	0	1	1	-3	0	0	0

Базис	B	x1	x2	x3	x4	x5	min
x3	1	1/2	-1/2	1	1/2	0	-
x5	5	1/2	21/2	0	-11/2	1	2
F(X2)	3	21/2	-1/2	0	11/2	0	0

Окончательный вариант симплекс-таблицы:

Базис	B	x1	x2	x3	x4	x5
x3	2	3/5	0	1	1/5	1/5
x2	2	1/5	1	0	-3/5	2/5
F(X3)	4	23/5	0	0	11/5	1/5

Оптимальный план можно записать так:

x₃ = 2

x₂ = 2

F(X) = 3•2 + -1•2 = 4

Білет №20

1.Стандартом передбачається, що октанове число бензину А-76 має бути не нижчим 76, а вміст сірки – не більшим, ніж 0,3 %. Для виготовлення такого бензину на заводі використовуються чотири компоненти. Дані про обсяги запасів компонентів, які змішуються, їх вартості, октанові числа та вміст сірки наведені в табл. 1:

Таблиця 1 – Техніко-економічні показники компонент бензину

Показник	Компонента бензину
	№ 1	№ 2	№ 3	№4
Октанове число	68	72	80	90
Вміст сірки, %	0,35	0,35	0,30	0,20
Наявний обсяг, т	700	600	500	300
Вартість, грош. од./т	40	45	60	90

Необхідно визначити, скільки тонн кожного компонента потрібно використати для того, щоб отримати 1000 т бензину А-76 з мінімальною собівартістю.

Побудувати економіко-математичну модель задачі.