БИЛЕТ№1

ЗАДАЧА №1

Розв’язати наступну задачу: компанія контролює три фабрики А₁, А₂, А₃, здатні виготовляти 150, 60 та 80 тис.од. продукції щотижня. Компанія уклала договір з чотирма замовниками В₁, В₂, В₃, В₄, яким потрібно щотижня відповідно 110, 40, 60 та 80 тис.од. продукції. Вартість виробництва та транспортування 1000 од. продукції замовниками з кожної фабрики наведено в таблиці.

Фабрика	Вартість виробництва і транспортування 1000 од. продукції за замовниками
	В1	В2	В3	В4
А1	4	4	2	5
А2	5	3	1	2
А3	2	1	4	2

Визначити для кожної фабрики оптимальний план перевезення продукції до замовників, що мінімізує загальну вартість виробництва і транспортних послуг.

Відповідь: Z₃ = 720 (ум. од.), .

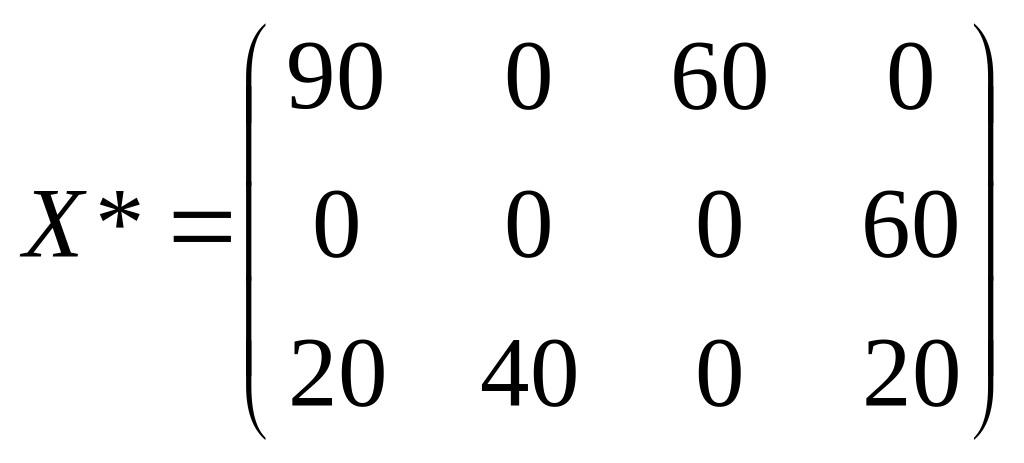Побудова математичної моделі. Нехай xij — кількість продукції, що перевозиться з і-ї фабрики до j-го замовника . Оскільки транспортна задача за умовою є збалансованою, закритою , то математична модель задачі матиме вигляд

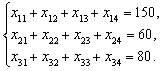
Економічний зміст записаних обмежень полягає ось у чому: уся вироблена на фабриках продукція має вивозитися до замовників повністю. Аналогічні обмеження можна записати відносно замовників: продукція, що надходить до споживача, має повністю задовольняти його попит. Математично це записується так: 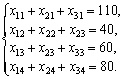Загальні витрати, пов’язані з виробництвом і транспортуванням продукції, складаються як добуток обсягу перевезеної продукції та питомої вартості перевезень за відповідним маршрутом і за умовою задачі мають бути мінімальними. Тому Z = 4 ? x11 + 4 ? x12 + 2 ? x13 + 5 ? x14 + 5 ? x21 + 3 ? x22 + x23 + + 2 ? x24 + 2 ? x31 + x32 +4 ? x33 +2 ? x34 ® min. 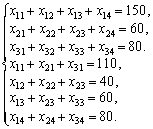У цілому математичну модель поставленої задачі можна записати так: Z = 4x11 + 4x12 + 2x13 + 5x14 + 5x21 + 3x22 + x23 + 2x24 + + 2x31 + x32 +4x33 +2x34 ® min Розв’язування.Розв’язування задачі подамо в таблицях, які назвемо транспортними. Перший опорний план задачі побудуємо методом мінімальної вартості.

Aj	Bj				ui
	B1= 110	B2= 40	B3= 60	B4= 80
A1= 150	4 110	4	2 2     +	5 40–	u1= 5
A2= 60	5	3	1 –60	2 0+	u2= 2
A3= 80	2	1 40	4	2 40	u3= 2
vj	v1= –1	v2= –1	v3= –1	v4= 0

Тому Z = 4 ? 110 + 5 ? 40 + 1 ? 60 + 1 ? 40 + 2 ? 40 = 820 ум. од. Перший опорний план транспортної задачі вироджений, оскільки кількість заповнених клітинок у таблиці дорівнює п’яти, а (m + n – 1) = 3 + 4 – 1 = 6. Для подальшого розв’язування задачі необхідно в одну з порожніх клітинок записати «нульове перевезення» так, щоб не порушити опорності плану, тобто можна зай­няти будь-яку вільну клітинку, яка не утворює замкненого циклу. Наприклад, заповнимо клітинку А2В4. Тепер перший план транспортної задачі є невиродженим, і його можна перевірити на оптимальність за допомогою методу потенціалів. На основі першої умови оптимальності ui + vj = cij складемо систему рівнянь для визначення потенціалів плану: 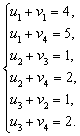Записана система рівнянь є невизначеною, і один з її розв’язків дістанемо, якщо, наприклад, v4 = 0. Тоді всі інші потенціали однозначно визначаються: u1 = 5, u2 = 2, u3 = 2, v1 = –1, v2 = –1, v3 = –1. Далі згідно з алгоритмом методу потенціалів перевіряємо виконання другої умови оптимальності ui + vj ? cij (для порожніх клітинок таблиці): А1B2: u1 + v2 = 5 + (–1) = 4 = 4; А1B3: u1 + v3 = 5 + (–1) = 4 > 2; А2B1: u2 + v1 = 2 + (–1) = 1 < 5; А2B2: u2 + v2 = 2 + (–1) = 1 < 3; А3B1: u3 + v1 = 2 + (–1) = 1 < 2; А3B3: u3 + v3 = 2 + (–1) = 1 < 4. Умова оптимальності не виконується для клітинки А1B3. Порушення D13 = (u1 + v3) – c13 = 4 – 2 = 2 записуємо в лівому нижньому кутку відповідної клітинки. Перший опорний план транспортної задачі є неоптимальним. Тому від нього необхідно перейти до другого плану, змінивши співвідношення заповнених і порожніх клітинок таблиці. Потрібно заповнити клітинку А1B3, в якій є єдине порушення умови оптимальності. Ставимо в ній знак «+». Для визначення клітинки, що звільняється, будуємо цикл, починаючи з клітинки А1B3, та позначаємо вершини циклу почергово знаками «–» і «+». Тепер необхідно перемістити продукцію в межах побудованого циклу. Для цього у вільну клітинку А1B3 переносимо менше з чисел хij, які розміщуються в клітинках зі знаком «–». Одночасно це саме число хij додаємо до відповідних чисел, що розміщуються в клітинках зі знаком «+», та віднімаємо від чисел, що розміщуються в клітинках, позначених знаком «–». У даному випадку , тобто . Виконавши перерозподіл продукції згідно із записаними правилами, дістанемо такі нові значення: клітинка А1B3 — 40 од. продукції, А2B3 – (60 – 40) = 20 од., А2B4 – (0 + 40) = 40 од. Клітинка А1B4, звільняється і в новій таблиці буде порожньою. Усі інші заповнені клітинки першої таблиці, які не входили до циклу, переписують у другу таблицю без змін. Кількість заповнених клітинок у новій таблиці також має відповідати умові невиродженості, тобто дорівнювати (n + m – 1). Отже, другий опорний план транспортної задачі матиме такий вигляд:

Aj	Bj				ui
	B1= 110	B2= 40	B3= 60	B4= 80
A1= 150	4 –110	4	2 40+	5	u1= 0
A2= 60	5	3	1 –20	2 40+	u2= –1
A3= 80	2 1   +	1 40	4	2 40–	u3= –1
vj	v1= 4	v2= –2	v3= 2	v4= 3

Тому Z2 = 4 ? 110 + 2 ? 40 + 1 ? 20 + 2 ? 40 + 1 ? 40 + 2 ? 40 = 740 ум. од. Новий план знову перевіряємо на оптимальність, тобто повторюємо описані раніше дії. Другий план транспортної задачі також неоптимальний (порушення для клітинки А3B1). За допомогою побудованого циклу виконаємо перехід до третього опор­ного плану транспортної задачі і дістанемо таку таблицю:

Aj	Bj				ui
	B1= 110	B2= 40	B3= 60	B4= 80
A1= 150	4 90	4	2 60	5	u1= 2
A2= 60	5	3	1	2 60	u2= 0
A3= 80	2 20	1 40	4	2 20	u3= 0
vj	v1= 2	v2= 1	v3= 0	v4= 2

Тому Z3 = 4 ? 90 + 2 ? 60 + 2 ? 60 + 2 ? 20 + 1 ? 40 + 2 ? 20 = 720 ум. од. Перевірка останнього плану на оптимальність за допомогою методу потенціалів показує, що він оптимальний. Тому ; За оптимальним планом перевезень перший замовник отримує 90 тис. од. продукції з першої фабрики та 20 тис. од. — з третьої. Другий споживач задовольняє свій попит за рахунок виробництва та перевезення 40 тис. од. продукції з третьої фабрики і т. д. При цьому загальна вартість виробництва та перевезення всієї продукції є найменшою і становить 720 ум. од

ЗАДАЧА №2

Побудувати двоїсту задачу до заданої задачі лінійного програмування.

Розв’язання. Пряму задачу зведемо до стандартного вигляду. Оскільки цільова функція Z мінімізується і в системі обмежень є нерівності, то вони мають бути виду « ». Тому друге обмеження задачі необхідно помножити на (–1). При цьому знак нерівності зміниться на протилежний. Отримаємо:

Двоїста задача:

Оскільки третє обмеження початкової задачі є рівнянням, то відповідна йому змінна двоїстої задачі може набувати як додатного, так і від’ємного значення.

БИЛЕТ№2

ЗАДАЧА №1

Фірмаспеціалізується на виробництвіофіснихмеблів, зокрема вона випускає два видизбірнихкнижковихполиць — А та В. Полиціобохвидіввиготовляють на верстатах 1 та 2. Тривалістьобробки деталей однієїполицікожноїмоделі подано в табл. (2.4).

Таблиця 2.4

ТРИВАЛІСТЬ ВИГОТОВЛЕННЯ КНИЖКОВИХ ПОЛИЦЬ

Верстат	Тривалістьобробкиполицімоделі, хв.		Ресурс робочого часу верстатів, год.на тиждень
	А	В
1	30	15	40
2	12	26	36

Прибутокфірмивідреалізаціїоднієїполицімоделі Адорівнює 50 у. о., а моделі В — 30 у. о. Вивчення ринку збуту показало, щотижневий попит на книжковіполицімоделі А ніколи не перевищуєпопиту на модель В більш як на 30 одиниць, а продаж полицьмоделі В не перевищує 80 одиниць на тиждень.

Необхідновизначитиобсягивиробництвакнижковихполицьцихдвох моделей, щомаксимізуютьприбутокфірми. Для цьогослідпобудуватиекономіко-математичну модель поставленоїзадачі та розв’язатиїїграфічно.

Побудоваматематичноїмоделі. Змінними в моделі є тижневіобсягивиробництвакнижковихполиць моделей А та В. Нехай х1 — кількістьполицьмоделі А, виготовленихфірмою за тиждень, а х2 — кількістьполицьмоделі В. Цільовафункціязадачі — максимум прибуткуфірмивідреалізаціїпродукції. Математично вона подається так:

.

Обмеженнязадачівраховуютьтривалістьроботиверстатів 1 та 2 для виготовленняпродукції та попит на полицірізних моделей.

Обмеження на тривалістьроботиверстатів 1 та 2 мають вид:

для верстата 1:

30х1 + 15х2 ≤ 2400 (хв);

для верстата 2:

12х1 + 26х2 ≤ 2160 (хв).

Обмеження на попит записуються так:

х1 – х2 ≤ 30 та х2 ≤ 80.

Загаломекономіко-математичну модель цієїзадачіможназаписати так:

maxZ = 50Х1 + 30Х2 (2.20)

за умов:

Цяекономіко-математична модель є моделлюзадачілінійногопрограмування, щоміститьлишедвізмінні, і тому може бути розв’язанаграфічно.

Розв’язання. Перший крокзгідно з графічним методом полягає в геометричномузображеннідопустимихпланівзадачі, тобто у визначеннітакоїобласті, де водночасвиконуютьсявсіобмеженнямоделі. Замінимо знаки нерівностей на знаки строгих рівностей і побудуємографікивідповіднихпрямих (рис. 2.14). Кожна з побудованихпрямихподіляєплощинусистеми координат на двіпівплощини. Координатиточокоднієї з півплощинзадовольняютьрозглядуванунерівність, а іншої — ні. Щобвизначитинеобхіднупівплощину (на рис. 2.14 їїнапрямпозначенострілкою), потрібновзяти будь-яку точку і перевірити, чизадовольняютьїїкоординатизазначенеобмеження. Якщозадовольняють, то півплощина, в якійміститьсявибрана точка, є геометричнимзображеннямнерівності. Інакше таким зображенням є іншапівплощина.

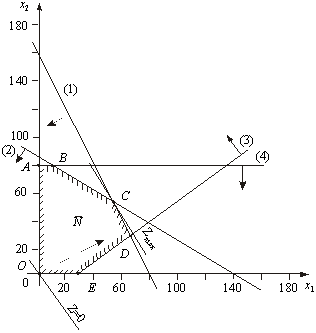
Рис. 2.14

Умованевід’ємностізміннихх1 ≥ 0, х2 ≥ 0 обмежує область допустимихпланівзадачі першим квадрантом системи координат. Перерізусіхпівплощинвизначає область допустимихпланівзадачі — шестикутникOABCDE. Координатибудь-якоїйого точки задовольняють систему обмеженьзадачі та умовуневід’ємностізмінних. Тому поставлену задачу буде розв’язано, якщо ми зможемовідшукатитаку точку багатокутникаOABCDE, вякійцільовафункціяZнабираєнайбільшогозначення.

Для цьогопобудуємо вектор , координатами якого є коефіцієнти при змінних у цільовійфункціїзадачі. Вектор завждивиходитьіз початку координат і напрямлений до точки з координатами (х1 = с1; х2 = с2). Унашійзадачі вектор . ВінзадаєнапрямзбільшеннязначеньцільовоїфункціїZ, а вектор, протилежниййому, — напрямїхзменшення.

Побудуємолінію, щовідповідає,наприклад, значеннюZ = 0. Це буде пряма 50х1 + 30х2 = 0, яка перпендикулярна до вектора і проходить через початок координат. Оскільки в даномуприкладінеобхідновизначитинайбільшезначенняцільовоїфункції, то пересуватимемопряму 50х1 + 30х2 = 0 паралельносамійсобізгідно з напрямом вектора доти, доки не визначимо вершину багатокутника, яка відповідає оптимальному плану задачі.

Із рис. 2.14 видно, щоостанньоюспільною точкою прямоїцільовоїфункції та багатокутникаOABCDE є точка С. Координатицієї точки є оптимальним планом задачі, тобтотакимиобсягамивиробництвакнижковихполицьвидів А та В, щозабезпечують максимум прибуткувідїхреалізації за даних умов.

Координати точки С є розв’язкомсистемирівнянь (2.17) і (2.18):

звідсимаємо: х1 = 50; х2 = 60.

Отже, Х* = (50; 60);

Цеозначає, що коли фірмащотижнявиготовлятиме 50 збірнихкнижковихполицьмоделі А та 60 — моделі В, то вона отримаємаксимальнийприбуток — 4300 у. о. Цепотребуватимеповноговикористаннятижневихресурсівробочого часу верстатів 1 та 2.

ЗАДАЧА №2

Однорідний вантаж, зосереджений у m постачальників в обсягах a_i ( ) необхідно поставити n споживачам в обсягах b_j ( ). Відомі с_ij ; ) – вартості перевезення одиниці вантажу від кожного i-го постачальника до кожного j-го споживача. Необхідно скласти такий план перевезень, при якому запаси усіх постачальників вивозяться повністю й сумарні витрати на перевезення усього вантажу мінімальні. Побудувати опорний план транспортної задачі методами мінімальної вартості, північно-західного кута.

a = (30; 50; 20);

b = (15; 15; 40; 30);

Розв’язування.Розв’язування задачі подамо в таблицях, які назвемо транспортними. Опорний план задачі побудуємо методом мінімальної вартості.

Aj	Bj
	B1= 15	B2= 15	B3=40	B4= 30
A1= 30	1 15	8	2 15	3
A2= 50	4	7	5 20	1 30
A3= 20	5	3 15	4 5	4

Опорний план задачі побудуємо методом північно-західного кута.

Aj	Bj
	B1= 15	B2= 15	B3=40	B4= 30
A1= 30	1 15	8 15	2	3
A2= 50	4	7	5 40	1 10
A3= 20	5	3	4	4 20

БИЛЕТ№3

ЗАДАЧА №1

Однорідний вантаж, зосереджений у m постачальників в обсягах a_i ( ) необхідно поставити n споживачам в обсягах b_j ( ). Відомі с_ij ; ) – вартості перевезення одиниці вантажу від кожного i-го постачальника до кожного j-го споживача. Необхідно скласти такий план перевезень, при якому запаси усіх постачальників вивозяться повністю й сумарні витрати на перевезення усього вантажу мінімальні. Побудувати опорний план транспортної задачі методами мінімальної вартості, північно-західного кута.

a = (40; 30; 35); b = (20; 34; 16; 10; 25);

Розв’язування.Розв’язування задачі подамо в таблицях, які назвемо транспортними. Опорний план задачі побудуємо методом мінімальної вартості.

Aj	Bj
	B1= 20	B2= 34	B3=16	B4= 10	B5= 25
A1= 40	2	6 5	3	4 10	8 25
A2= 30	1 20	5 10	6	9	7
A3= 35	3	4 19	1 16	6	10

Опорний план задачі побудуємо методом північно-західного кута.

Aj	Bj
	B1= 20	B2= 34	B3=16	B4= 10	B5= 25
A1= 40	2 20	6 20	3	4	8
A2= 30	1	5 14	6 16	9	7
A3= 35	3	4	1	6 10	10 25

ЗАДАЧА №2

Побудувати двоїсту задачу до заданої задачі лінійного програмування. Визначити оптимальні плани прямої та двоїстої задач.

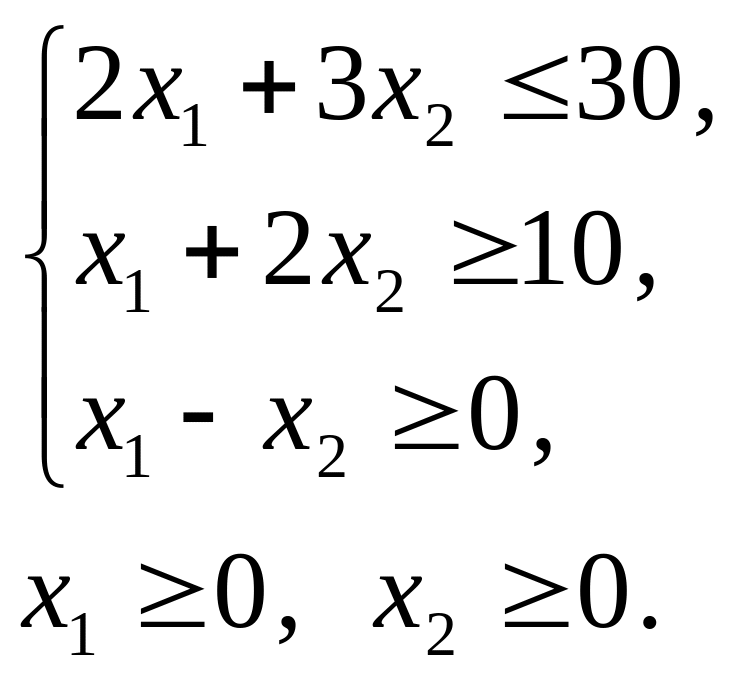
Розв’язання. Пряму задачу зведемо до стандартного вигляду. Оскільки цільова функція Z мінімізується і в системі обмежень є нерівності, то вони мають бути виду « ». Тому перше обмеження задачі необхідно помножити на (–1). При цьому знак нерівності зміниться на протилежний. Отримаємо:

Двоїста задача:

Двойственная задача линейного программирования.

Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы.

Определим минимальное значение целевой функции F(X) = 2x₁ + 3x₂ при следующих условиях-ограничений.

2x₁ + 3x₂≤30

x₁ + 2x₂≥10

x₁ - x₂≥0

Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).

В 1-м неравенстве смысла (≤) вводим базисную переменную x₃. В 2-м неравенстве смысла (≥) вводим базисную переменную x₄ со знаком минус. В 3-м неравенстве смысла (≥) вводим базисную переменную x₅ со знаком минус.

2x₁ + 3x₂ + 1x₃ + 0x₄ + 0x₅ = 30

1x₁ + 2x₂ + 0x₃-1x₄ + 0x₅ = 10

1x₁-1x₂ + 0x₃ + 0x₄-1x₅ = 0

Введем искусственные переменные x: в 2-м равенстве вводим переменную x₆; в 3-м равенстве вводим переменную x₇;

2x₁ + 3x₂ + 1x₃ + 0x₄ + 0x₅ + 0x₆ + 0x₇ = 30

1x₁ + 2x₂ + 0x₃-1x₄ + 0x₅ + 1x₆ + 0x₇ = 10

1x₁-1x₂ + 0x₃ + 0x₄-1x₅ + 0x₆ + 1x₇ = 0

Для постановки задачи на минимум целевую функцию запишем так:

F(X) = 2x₁+3x₂+Mx₆+Mx₇ → min

За использование искусственных переменных, вводимых в целевую функцию, накладывается так называемый штраф величиной М, очень большое положительное число, которое обычно не задается.

Полученный базис называется искусственным, а метод решения называется методом искусственного базиса.

Причем искусственные переменные не имеют отношения к содержанию поставленной задачи, однако они позволяют построить стартовую точку, а процесс оптимизации вынуждает эти переменные принимать нулевые значения и обеспечить допустимость оптимального решения.

Из уравнений выражаем искусственные переменные:

x₆ = 10-x₁-2x₂+x₄

x₇ = 0-x₁+x₂+x₅

которые подставим в целевую функцию:

F(X) = 2x₁ + 3x₂ + M(10-x₁-2x₂+x₄) + M(0-x₁+x₂+x₅) → min

или

F(X) = (2-2M)x₁+(3-1M)x₂+(1M)x₄+(1M)x₅+(10M) → min

Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:

2	3	1	0	0	0	0
1	2	0	-1	0	1	0
1	-1	0	0	-1	0	1

Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом.

Решим систему уравнений относительно базисных переменных:

x₃, x₆, x₇,

Полагая, что свободные переменные равны 0, получим первый опорный план:

X1 = (0,0,30,0,0,10,0)

Базисное решение называется допустимым, если оно неотрицательно.

Базис	B	x1	x2	x3	x4	x5	x6	x7
x3	30	2	3	1	0	0	0	0
x6	10	1	2	0	-1	0	1	0
x7	0	1	-1	0	0	-1	0	1
F(X0)	10M	-2+2M	-3+1M	0	-1M	-1M	0	0

Переходим к основному алгоритму симплекс-метода.

Итерация №0.

1. Проверка критерия оптимальности.

Текущий опорный план неоптимален, так как в индексной строке находятся положительные коэффициенты.

2. Определение новой базисной переменной.

В качестве ведущего выберем столбец, соответствующий переменной x₁, так как это наибольший коэффициент .

3. Определение новой свободной переменной.

Вычислим значения D_i по строкам как частное от деления: b_i / a_i1

и из них выберем наименьшее:

min (30 : 2 , 10 : 1 , 0 : 1 ) = 0

Следовательно, 3-ая строка является ведущей.

Разрешающий элемент равен (1) и находится на пересечении ведущего столбца и ведущей строки.

Базис	B	x1	x2	x3	x4	x5	x6	x7	min
x3	30	2	3	1	0	0	0	0	15
x6	10	1	2	0	-1	0	1	0	10
x7	0	1	-1	0	0	-1	0	1	0
F(X1)	10M	-2+2M	-3+1M	0	-1M	-1M	0	0	0

4. Пересчет симплекс-таблицы.

Формируем следующую часть симплексной таблицы.

Вместо переменной x в план 1 войдет переменная x₁ .

Строка, соответствующая переменной x₁ в плане 1, получена в результате деления всех элементов строки x₇ плана 0 на разрешающий элемент РЭ=1

На месте разрешающего элемента в плане 1 получаем 1.

В остальных клетках столбца x₁ плана 1 записываем нули.

Таким образом, в новом плане 1 заполнены строка x₁ и столбец x₁ .

Все остальные элементы нового плана 1, включая элементы индексной строки, определяются по правилу прямоугольника.

Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.

НЭ = СЭ - (А*В)/РЭ

СТЭ - элемент старого плана, РЭ - разрешающий элемент (1), А и В - элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ.

Представим расчет каждого элемента в виде таблицы:

B	x 1	x 2	x 3	x 4	x 5	x 6	x 7
30-(0 • 2):1	2-(1 • 2):1	3-(-1 • 2):1	1-(0 • 2):1	0-(0 • 2):1	0-(-1 • 2):1	0-(0 • 2):1	0-(1 • 2):1
10-(0 • 1):1	1-(1 • 1):1	2-(-1 • 1):1	0-(0 • 1):1	-1-(0 • 1):1	0-(-1 • 1):1	1-(0 • 1):1	0-(1 • 1):1
0 : 1	1 : 1	-1 : 1	0 : 1	0 : 1	-1 : 1	0 : 1	1 : 1
(0)-(0 • (-2+2M)):1	(-2+2M)-(1 • (-2+2M)):1	(-3+1M)-(-1 • (-2+2M)):1	(0)-(0 • (-2+2M)):1	(-1M)-(0 • (-2+2M)):1	(-1M)-(-1 • (-2+2M)):1	(0)-(0 • (-2+2M)):1	(0)-(1 • (-2+2M)):1

Получаем новую симплекс-таблицу:

Базис	B	x1	x2	x3	x4	x5	x6	x7
x3	30	0	5	1	0	2	0	-2
x6	10	0	3	0	-1	1	1	-1
x1	0	1	-1	0	0	-1	0	1
F(X1)	10M	0	-5+3M	0	-1M	-2+1M	0	2-2M

Итерация №1.

1. Проверка критерия оптимальности.

Текущий опорный план неоптимален, так как в индексной строке находятся положительные коэффициенты.

2. Определение новой базисной переменной.

В качестве ведущего выберем столбец, соответствующий переменной x₂, так как это наибольший коэффициент .

3. Определение новой свободной переменной.

Вычислим значения D_i по строкам как частное от деления: b_i / a_i2

и из них выберем наименьшее:

min (30 : 5 , 10 : 3 , - ) = 3¹/₃

Следовательно, 2-ая строка является ведущей.

Разрешающий элемент равен (3) и находится на пересечении ведущего столбца и ведущей строки.

Базис	B	x1	x2	x3	x4	x5	x6	x7	min
x3	30	0	5	1	0	2	0	-2	6
x6	10	0	3	0	-1	1	1	-1	31/3
x1	0	1	-1	0	0	-1	0	1	-
F(X2)	10M	0	-5+3M	0	-1M	-2+1M	0	2-2M	0