1)Матриця — математичний об'єкт, записаний у вигляді прямокутної таблиці чисел (чи елементів кільця), він допускає операції (додавання, віднімання, множення тамноження на скаляр). Зазвичай матриці представляються двовимірними (прямокутними) таблицями. Іноді розглядають багатовимірні матриці або матриці непрямокутної форми. В цій статті вони розглядатися не будуть.
Додавання
Якщо дано дві матриці m-на-n A і B, можемо означити їх суму A + B як матрицю m-на-n, що утворюється додаванням відповідних елементів, себто,
Множення на скаляр
Якщо дано матрицю A і число c, можемо означити множення на скаляр cA як (cA)[i, j] = cA[i, j]. Наприклад,
З цими двома операціями множина M(m, n, R) усіх матриць m-на-n з дійсними елементами є дійсним векторним простором розмірності mn.
Множення матриць
Множення двох матриць має сенс лише тоді, коли число стовпчиків першої матриці дорівнює числу рядків другої матриці. Якщо A — матриця m-на-n (m рядків, n стовпчиків), а B — матриця n-на-p (n рядків, p стовпчиків), їх добуток AB є матрицею m-на-p (m рядків, pстовпчиків), що розраховується за формулою:
Це множення має такі властивості:
(AB)C = A(BC) для всіх матриць A розмірності k-на-m, B розмірності m-на-n і C розмірності n-на-p (асоціативність).
(A + B)C = AC + BC для всіх матриць A і B розмірності m-на-n і матриць C розмірності n-на-k (дистрибутивність).
C(A + B) = CA + CB для всіх матриць A і B розмірності m-на-n і матриць C розмірності k-на-m (дистрибутивність).
Зауваження: комутативність має місце не завжди: для добутку певних матриць A і B може бути AB ≠ BA.
Матриці називають антикомутативними, якщо AB = −BA. Такі матриці є дуже важливими в представленнях алгебр Лі та в представленнях алгебр Кліффорда.
2)Визначення
Визначник
матриці ![]() задається
формулою:
задається
формулою:
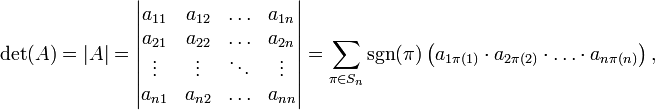
де ![]() — перестановка множини
— перестановка множини ![]() і
і ![]() це
знак (або парність) перестановки, тобто
дорівнює 1 чи -1 залежно від парності
числа інверсій
це
знак (або парність) перестановки, тобто
дорівнює 1 чи -1 залежно від парності
числа інверсій ![]()
Кількість
доданків у сумі дорівнює ![]() і
номери рядка та стовпця елементів
матриці, що входять у один добуток, не
повторюються.
і
номери рядка та стовпця елементів
матриці, що входять у один добуток, не
повторюються.
Матриця називається виродженою, якщо її визначник дорівнює нулю, а в іншому випадку невиродженою.
Визначник 2×2 матриці
Щоб
знайти визначник ![]() матриці,
множимо елементи головної
діагоналі та
віднімаємо добуток елементів побічної
діагоналі:
матриці,
множимо елементи головної
діагоналі та
віднімаємо добуток елементів побічної
діагоналі:
![]()
[ред.]Визначник 3×3 матриці
Щоб
знайти визначник ![]() матриці,
будуємо шість добутків таким чином:
матриці,
будуємо шість добутків таким чином:
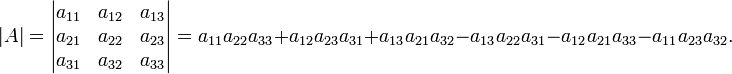
Для
знаходження визначників високого
порядку застосовуються принципово інші
методи (насамперед, метод
Гауса),
що вимагають значно меншої кількості
арифметичних операцій (![]() замість
замість ![]() )
)
Властивості
Якщо помножити якийсь рядок на константу
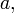 то
визначник також помножиться на
то
визначник також помножиться на 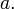
Якщо у матриці поміняти місцями будь-які два рядки, то знак визначника зміниться на протилежний.
При додаванні до будь-якого рядка лінійної комбінації кількох інших рядків визначник не зміниться.
У матриці з двома однаковими рядками або з нульовим рядком, визначник дорівнює нулю.
Всі властивості визначників, що стосуються рядків, так само справедливі і для стовпців.
Визначник трикутної матриці дорівнює добутку елементів на діагоналі.
Теорема Лапласа: визначник квадратної матриці дорівнює сумі добутків елементів деякого рядка на відповідні їм алгебраїчні доповнення.
Лема про фальшивий розклад: сума добутків елементів деякого рядка на алгебраїчні доповнення відповідних елементів паралельного рядка дорівнює нулю.
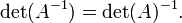
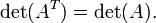

В лінійній
алгебрі доводиться,
що перші три властивості майже
характеризують визначник матриць з
елементами у полі.
А саме, якщо функція елементів матриці
задовільняє 1,2,3, то така функція
пропорціональна ![]() .
.
4. метод крамера
Опис методу
Для
системи ![]() лінійних
рівнянь з
невідомими
(над довільним полем)
лінійних
рівнянь з
невідомими
(над довільним полем)

з
визначником матриці системи ![]() ,
що не рівний нулю, розв'язок записується
у такому вигляді:
,
що не рівний нулю, розв'язок записується
у такому вигляді:
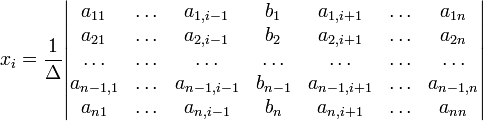
(i-й стовпчик матриці системи замінюється стовпчиком вільних членів). Іншим чином правило Крамера формулюється так: для будь-яких коефіцієнтів c1, c2, …, cn виконується рівність:

У такій
формі формула Крамера справедлива без
припущення, що
не
рівне нулю, не треба навіть, аби коефіцієнти
системи були елементами цілісного
кільця (визначник системи навіть може
бути дільником нуля у кільці коефіцієнтів).
Також можна вважати, що або набори ![]() та
та ![]() ,
або набір
,
або набір ![]() складаються
не з елементів кільця коефіциєнтів
системи, а деякого модуля над
цим кільцем. В такому вигляді формула
Крамера використовується, наприклад,
при доведенні формули для визначника
Грама і Леми
Накаями.
складаються
не з елементів кільця коефіциєнтів
системи, а деякого модуля над
цим кільцем. В такому вигляді формула
Крамера використовується, наприклад,
при доведенні формули для визначника
Грама і Леми
Накаями.
5. метод гаусса
Ме́тод Га́уса — алгоритм розв'язку системи лінійних алгебраїчних рівнянь.
Початок
алгоритму. 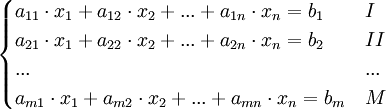
Прямий хід: Шляхом елементарних перетворень рядків (додавань до рядка іншого рядка, помноженого на число, і перестановок рядків) матриця приводиться доверхньотрикутного вигляду.
З цього моменту починається зворотний хід.
З останнього ненульового рівняння виражаємо кожну з базисних змінних через небазисні і підставляємо в попередні рівняння. Повторюючи цю процедуру для всіх базисних змінних, отримуємо фундаментальний розв'язок.
6. обернена матриця
Обернена
матриця — матриця (позначається ![]() ),
яка існує для кожної невиродженої квадратної матриці
,
розмірності
),
яка існує для кожної невиродженої квадратної матриці
,
розмірності ![]() ,
причому:
,
причому:
![]()
де ![]() одинична
матриця.
одинична
матриця.
Якщо для матриці існує , то така матриця називається оборотною, тобто кожна невироджена матриця є оборотною, і навпаки — кожна оборотна матриця є невиродженою.
7. вектори на площині
Вектор - це напрямлений відрізок або вектор - це паралельний перенос.
Вектори
позначають:![]()
|
|
|
|
Або за початком і кінцем
|
|
|
|
Якщо початок і кінець співпадають, вектор називають нульовим або О Два вектори називають рівними, якщо їх довжини рівні, а напрями співпадають

Вектори, які лежать на паралельних прямих, називають колінеарними.
|
|
|
|
(а якщо ця умова не виконується, то не колінеарними)
![]()
Вектори, які лежать в одній площині, називають компланарними (а якщо
ц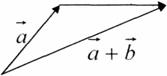 я
умова не виконується, не компланарними).
я
умова не виконується, не компланарними).
![]()
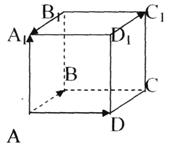 -
не компланарні
-
не компланарні
![]() -
компланарні
-
компланарні
2. Додавання векторів Правило трикутника
П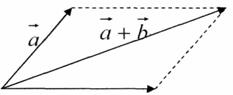 равило
паралелограма
равило
паралелограма
Сумою двох не колінеарних векторів, що виходять з однієї точки, є діагональ паралелограма, побудованого на цих векторах, яка виходить з цієї ж точки.
Правило паралелепіпеда
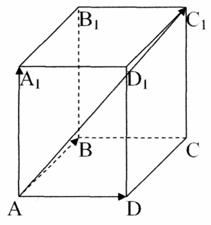
Сумою трьох не колінеарних векторів, що виходять з однієї точки, є діагональ паралелепіпеда, побудованого на цих векторах, яка виходить з цієї ж точки.
Властивості додавання
1) ![]() —
комутативність
—
комутативність
2) ![]() —
асоціативність
—
асоціативність
3) ![]()
4)
якщо ![]() ,
то
,
то ![]() і
називається протилежним
і
називається протилежним
Віднімання векторів
Щоб відняти два вектори, потрібно відкласти їх від спільної точки, з'єднати кінці і стрілку поставити до того вектора, від якого віднімаємо
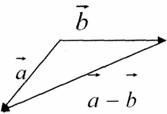
Множення вектора на число.
Добутком ![]() на
число k називають вектор, який має
довжину
на
число k називають вектор, який має
довжину ![]() і
співнапрямлений з
,
якщо k > 0 та протилежний до нього, якщо
k < 0.
і
співнапрямлений з
,
якщо k > 0 та протилежний до нього, якщо
k < 0.
|
|
|
|
Як видною, при множенні вектора на число, одержуємо колінеарні вектори. Справедливе обернене твердження, яке?.
Скалярний добуток векторів.
Скалярним добутком двох векторів називають число, що дорівнює добутку довжин цих векторів на косинус кута між ними.
![]() ,
де
,
де ![]()


Якщо ![]() то
то ![]() і
навпаки , якщо
і
навпаки , якщо ![]() ,
тобто
.
,
тобто
.
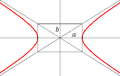
8. Гіпербола
Гіпербола (грец. ὑπερβολή) — крива другого порядку з ексцентриситетом більшим за одиницю.
Визначення
Гіпербола є невиродженою кривою другого порядку, яка задається рівнянням:[1]
![]()
де ![]() та
та ![]() —
параметри. Таке рівняння називається канонічним
рівнянням гіперболи.[2]
—
параметри. Таке рівняння називається канонічним
рівнянням гіперболи.[2]
Нехай канонічне рівняння кривої другого порядку шляхом переносу центру координат перетворено у вигляд:
![]()
В цьому
випадку крива проходить через початок
координат нової системи; вісь абсцис є
віссю симетрії кривої. Це рівняння
відображає той факт, що невироджена
крива другого порядку є геометричним
місцем точок, відношення відстаней
яких ![]() (ексцентриситет)
від заданої точки (фокуса)
та від заданої прямої (директриса)
незмінна. Крива є гіперболою,
якщо
(ексцентриситет)
від заданої точки (фокуса)
та від заданої прямої (директриса)
незмінна. Крива є гіперболою,
якщо ![]() .[1] Тобто,
гіпербола є геометричним місцем точок,
абсолютна величина різниці відстаней
яких від фокусів дорівнює
.[1] Тобто,
гіпербола є геометричним місцем точок,
абсолютна величина різниці відстаней
яких від фокусів дорівнює ![]() (фокальна
властивість гіперболи). Директоріальна
властивість гіперболи полягає в тому,
що гіпербола є геометричним місцем
точок, відношення відстаней яких від
фокуса до одноіменної директриси
дорівнює
(фокальна
властивість гіперболи). Директоріальна
властивість гіперболи полягає в тому,
що гіпербола є геометричним місцем
точок, відношення відстаней яких від
фокуса до одноіменної директриси
дорівнює ![]() .[2]
.[2]
Властивості
Гіпербола та її фокуси.
Гіпербола та її напіввіссі та асимптоти.
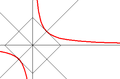
Рівнобічна гіпербола.
|
Якщо
в канонічному рівнянні гіперболи ![]() ,
то гіпербола називається рівнобічною.
В координатах
,
то гіпербола називається рівнобічною.
В координатах
![]()
рівняння рівнобічної гіперболи
![]()
матиме вигляд:
![]()
звідки
випливає, що по відношенню до
координат ![]() та
та ![]() рівнобічна
гіпербола представляє собою
графік звортньо-пропорційної
залежності.
В координатах
рівнобічна
гіпербола представляє собою
графік звортньо-пропорційної
залежності.
В координатах ![]() та
та ![]() маємо
такий саме графік обернений на кут
маємо
такий саме графік обернений на кут ![]() .[2]
.[2]
При ![]() (а
також при
(а
також при ![]() )
графік зворотньо-пропорційної залежності
щільніше притіскається до осі
абсцис
)
графік зворотньо-пропорційної залежності
щільніше притіскається до осі
абсцис ![]() (відповідно,
до осі ординат
(відповідно,
до осі ординат ![]() ),
оскільки ці осі є асимптотами (двобічними)
графіку. В канонічних координатах
,
ці
асимптоти є бісектрисами
),
оскільки ці осі є асимптотами (двобічними)
графіку. В канонічних координатах
,
ці
асимптоти є бісектрисами ![]() та
та ![]() координатних
кутів.
координатних
кутів.
З гіперболою пов'язані такі числові властивості:
число
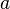 ,
що зветься дійсною
напіввіссю;
,
що зветься дійсною
напіввіссю;число
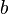 ,
що зветься уявною
напіввіссю;
,
що зветься уявною
напіввіссю;число
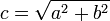 ,
що зветься лінійним
ексцентриситетом;
,
що зветься лінійним
ексцентриситетом;число
 ,
що зветься фокусною
відстаню;
,
що зветься фокусною
відстаню;число
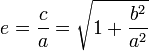 ,
що називається числовим
ексцентриситетом;
,
що називається числовим
ексцентриситетом;число
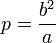 ,
що зветься фокальним
параметром;
,
що зветься фокальним
параметром;вісь абсцис, що зветься дійсною (або фокальною) віссю;
вісь ординат, що зветься уявною віссю;
точка
 ,
що зветься центром;
,
що зветься центром;точки
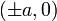 ,
що звуться вершинами;
,
що звуться вершинами;точки
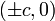 ,
що звуться фокусами;
,
що звуться фокусами;прямі
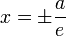 ,
що звуться директрисами.
,
що звуться директрисами.
9. Парабола
Пара́бола (від грец. παραβολή) — геометричне місце точок, що рівновіддалені від точки і прямої. Одна з кривих другого порядку.
Точка зветься фокусом, а пряма - директрисою.
Парабола, гіпербола та еліпс є конічними перерізами. Парабола є конічним перерізом з одиничним ексцентриситетом.Якщоточкове джерело світла розміщене у фокусі параболоїдного дзеркала, то відбиті від поверхні промені будуть розповсюджуватисяпаралельно.
Графік функції, що задається за допомогою поліному другого порядку від однієї змінної являє собою параболу.
Рівняння
Канонічне рівняння параболи в прямокутній системі координат:
![]() (або
(або ![]() ,
якщо поміняти місцями осі).
,
якщо поміняти місцями осі).
Квадратне
рівняння ![]() при
при ![]() також
представляє собою параболу і графічно
зображаєтся тією ж параболою, що і
також
представляє собою параболу і графічно
зображаєтся тією ж параболою, що і ![]() ,
але на відміну від останньої має вершину
не в початку координат, а в деякій
точці
,
але на відміну від останньої має вершину
не в початку координат, а в деякій
точці ![]() ,
координати якої обчислюються за
формулами :
,
координати якої обчислюються за
формулами :
![]()
Рівняння
може
бути представлено у вигляді ![]() ,
а у випадку переносу початку координат
в точку
канонічним
рівнянням. Таким чином для кожного
квадратного рівняння можна найти систему
координат таку, що в цій системі воно
представиться канонічним.
,
а у випадку переносу початку координат
в точку
канонічним
рівнянням. Таким чином для кожного
квадратного рівняння можна найти систему
координат таку, що в цій системі воно
представиться канонічним.
Розрахунок коефіцієнтів квадратного рівняння
Якщо
для рівняння
відомі
координати 3-х різних точок його
графіка ![]() ,
, ![]() ,
, ![]() ,
то його коефіцієнти можуть бути знайдені
так:
,
то його коефіцієнти можуть бути знайдені
так:
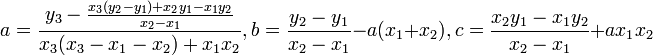
Властивості
Парабола - крива другого порядку.
Вона має вісь симетрії, що називається віссю параболи. Вісь проходить через фокус і перпендикулярна директрисі.
Оптична властивість. Пучок променів, паралельних осі параболи, відбиваючись у параболі, збирається в її фокусі. І навпаки, світло від джерела, що знаходиться у фокусі, відображається параболою в пучок паралельних її осі променів.
Для параболи
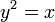 фокус
знаходиться в точці (0,25; 0).
фокус
знаходиться в точці (0,25; 0).Якщо фокус параболи відобразити щодо дотичній, то його образ буде лежати на директрисі.
Парабола є антиподерою прямій.
Всі параболи подібні. Відстань між фокусом і директрисою визначає масштаб.
При обертанні параболи навколо осі симетрії виходить еліптичний параболоїд.
Еволютою параболи є напівкубічна парабола.
10. Вектори у просторі
Координати і вектори в просторі
|
Прямокутна (декартова) система координат в просторі задається трійкою попарно перпендикулярних осей. Відстань між двома точками A(XA; YA; ZA) i B(XB; YB; ZB) в просторі визначається формулою:
Якщо С(XС; YС; ZС) – середина відрізка AB, то
|
Якщо
вектор a, який знаходиться в прямокутній
системі координат OXYZ, має початком точку
A з координатами XA,
YA,
ZA,
а кінцем – точку B з координатами XB,
YB,
ZB,
то числа XB -
XA,
YB -
YA,
ZB -
ZA називається
його координатами: a( XB -
XA;
YB -
YA;
ZB -
ZA).
Довжина
(модуль) цього вектора:
![]()
Сумою векторів a(XA; YA; ZA) і b(XB; YB; ZB) називається вектор c(XA + XB; YA + YB; ZA + ZB).
Добутком вектора a(XA; YA; ZA) на число λ називається вектор λa(λXA; λYA; λZA).
Скалярним добутком векторів a та b, якщо відомі їх координати, є величина a•a = XA•XB + YA•YB + ZA•ZB.
Для кута φ між векторами a та b:

11. Рівняння прямої на площині
Рівняння прямої з кутовим коефіцієнтом
Рівняння прямої в відрізках на осях
Рівняння прямої, що проходить через дві різні точки на площині
Параметричне рівняння прямої на площині
Канонічне рівняння прямої на площині
Рівняння прямої на площині
Будь-яку пряму на площині можна задати рівнянням прямої першого ступеня вигляду
A x + B y + C = 0
Де A і B не можуть одночасно дорівнювати нулю.
Дві площини називаються перпендикулярними, якщо двогранний кут між ними дорівнює 90 градусам. Теорема 1. Якщо дві прямі, які перетинаються, паралельні відповідно двом іншим перпендикулярним прямим, то інші прямі теж перпендикулярні. Теорема 2. Через будь-яку точку прямої у просторі можна провести безліч перпендикулярних до неї прямих (див. рисунок). (Усі прямі лежать у площині, яка перпендикулярна до даної прямої і перетинає її у даній точці.)
Паралельними (рівнобіжними) прямими називають прямі, котрі лежать в одній площині і або збігаються, або не перетинаються. В деяких шкільних означеннях, щоправда, паралельні прямі не можуть збігатись, але тут цей факт не береться до уваги.
Властивості
Паралельність — Бінарне відношення еквівалентності, тому разбиває всю множину прямих на класи паралельних між собою.
Через довільну точку можна провести лише одну пряму, паралельную даній. Це властивість евклідової геометрії, в інших геометріях число 1 замінено іншими (в геометрії Лобачевского таких прямих минімум дві).
Дві паралельні прямі в просторі лежать в одній площині.
При перетині двох паралельних прямих третьою, т. зв. січною:
Січна обов'язково перетинає обидві прямі.
При перетині утворюється 8 кутів, при чому деякі характерні їх пари мають особливі назви та властивості:
Перехресні кути рівні.
Відповідні кути рівні.
Односторонні кути в сумі становлять 180°.
І, очевидно, суміжні кути в сумі становлять 180°, а вертикальні — рівні.
Термін походить від грец. ἔλλειψις — нестача, пропуск, випадіння (мається на увазі «неповнота» або «дефектність» еліпсу порівняно з «повним» колом або кругом).
Канонічне рівняння еліпса
![]()
[ред.]Параметричне рівняння еліпса
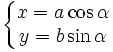
[ред.]Нормальне рівняння еліпса
![]()
Ко́ло — геометричне місце точок площини, відстань від яких до заданої точки, що називається центром кола, є постійною величиною і дорівнюєрадіусу кола.
Коло з центром у точці О і радіусом r позначають О(r).
Коло
на площині, даного радіуса ![]() ,
у певній вибраній декартовій
системі координат
і
,
з центром в точці (a, b)
описується стандартним рівнянням:
,
у певній вибраній декартовій
системі координат
і
,
з центром в точці (a, b)
описується стандартним рівнянням:
![]()
Це рівняння випливає з теореми Піфагора, при її застовуванні до кожної точки кола, як показано на рисунку справа, де радіус цегіпотенуза прямокутного трикутника, катети якого x − a та y − b. Якщо центр кола знаходиться в початку координат (0, 0), тоді рівняння спрощується до такого вигляду:
![]()
Загальне рівняння кола:
![]()
Загальне рівняння площини
Будь-яку площину можна задати рівнянням площини першого ступеня вигляду Ax+ By+ C z + D= 0 де A, B і C не можуть одночасно дорівнювати нулю.
Рівняння площини в відрізках
Якщо площина перетинає осі OX, OY і OZ в точках з координатами (a, 0, 0), (0, b, 0) і (0, 0, с), то вона може бути знайдена, якщо використати формулу рівняння площини в відрізках
x |
+ |
y |
+ |
z |
= 1 |
a |
b |
c |
Рівняння площини, що проходить через точку, перпендикулярно вектору нормалі
Щоб скласти рівняння площини, за координатами точки площини M(x0, y0, z0) і вектора нормалі площини n = {A; B; C} можна використати наступну формулу.
A(x - x0) + B(y - y0) + C(z - z0) = 0
Рівняння площини, що проходить через три задані точки, які не лежать на одній прямій
Якщо задані координати трьох точок A(x1, y1, z1), B(x2, y2, z2) і C(x3, y3, z3), які лежать на площині, то рівняння площини можна знайти за наступною формулою
x-x1 y-y1 z-z1
x2-x1 y2-y1 z2-z1 = 0
x3-x1 3y-y1 z3-z1
Площина — алгебраїчна поверхня першого порядку: в декартовій системі координат площина може бути задана рівнянням першого степеня.
15)
Взаємне розміщення двох прямих в
просторі
|
|
|
|