Задания 13, 18, 23, 28, 33, 38

Построить в трех проекциях геометрические тела. Найти проекции точек, расположенных на их поверхностях.

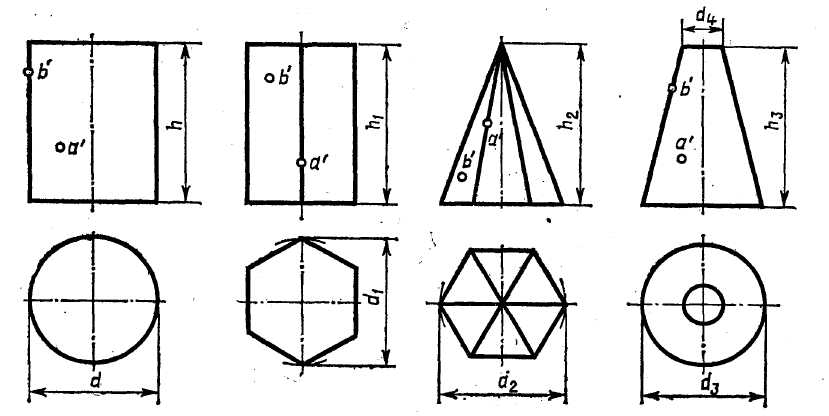
№ задания	13	18	23	28	33	38
d	40	48	44	42	46	50
d1	50	44	42	48	40	40
d2	40	42	48	50	42	44
d 3	40	50	46	40	50	40
h	40	50	60	50	60	50
h1	50	60	50	55	50	60
h2	60	50	50	55	55	50
h3	60	60	55	50	55	60

Задания 14, 19, 24, 29, 34, 39

Построить в трех проекциях геометрические тела. Найти проекции точек, расположенных на их поверхностях.

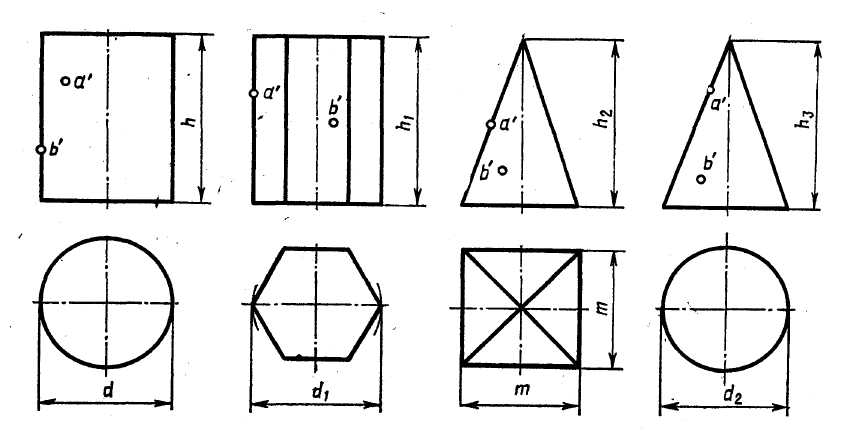
№ задания	14	19	24	29	34	39
d	40	46	42	44	40	48
d1	50	46	50	40	48	44
d2	40	46	40	42	46	42
m	25	20	25	20	20	25
h	60	50	50	60	55	50
h1	50	60	50	50	60	55
h2	60	60	50	60	55	60
h3	60	60	50	60	60	55

Методические указания к листу 1-3.

На листе 1-3 необходимо выполнить комплексный чертеж геометрического тела, пересеченного проецирующей плоскостью, построить действительную фигуру сечения, вычертить развертку и геометрическую проекцию усеченного геометрического тела. Образец выполнения листа 1-3 показан на рис. 17, 18.

Сечение призмы плоскостью

Фигура сечения прямой пятигранной призмы фронтально-проецирующей плоскостью Р (рис. 15, а и б) представляет собой плоский пятиуголь­ник 1 2 3 4 5.

Для построения проекций фигуры сечения нахо­дят проекции точек пересечения плоскости Р с ре­брами призмы и соединяют их прямыми линиями. Фронтальные проекции этих точек получаются при пересечении фронтальных проекций ребер призмы со следом P_v плоскости Р (точки 1'-5').

Горизонтальные проекции точек пересечения 1-5 совпадают с горизонтальными проекциями ребер. Имея две проекции этих точек, с помощью линий связи находят профильные проекции 1"-5". Полу­ченные точки 1" -5" соединяют прямыми линиями и получают профильную проекцию фигуры сечения.

Действительный вид фигуры сечения можно определить любым из способов: вращения, совме­щения или перемены плоскостей проекций.

Рис. 15 – Сечение призмы плоскостью

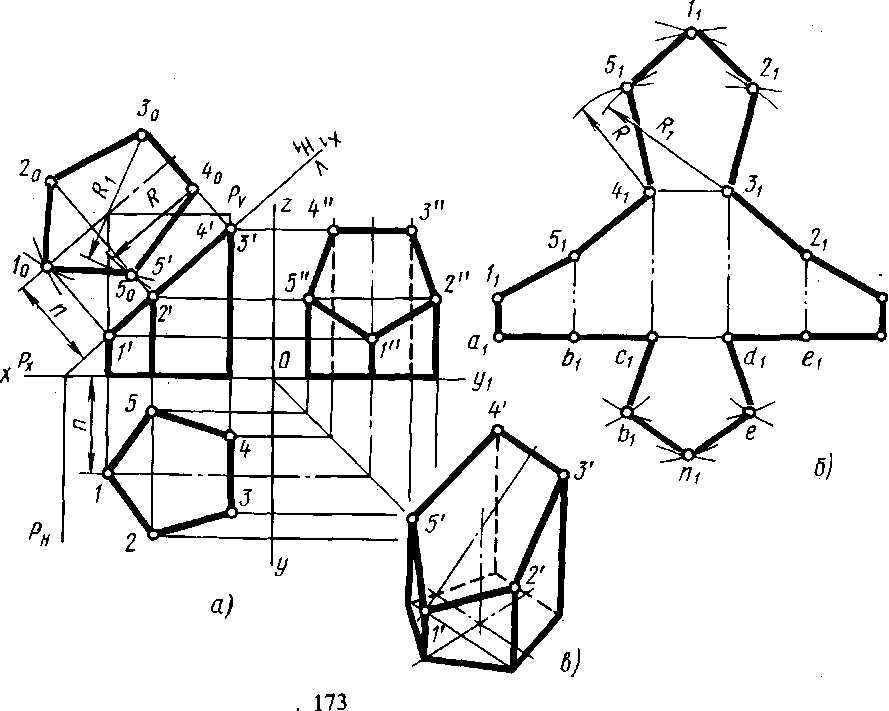
В данном примере (рис. 15, а) применен способ перемены плоскостей проекций. Горизонтальная плоскость проекций заменена новой Н₁, причем ось x₁ (для упрощения построений) совпадает с фрон­тальным следом плоскости Р.

Для нахождения новой горизонтальной проекции какой-либо точки фигуры сечения (например, точки 1) необходимо выполнить следующие построения. Из точки 1' восставляют перпендикуляр к новой оси х₁ и откладывают на нем расстояние от пре­жней оси х до прежней горизонтальной проекции точки 1, т.е. отрезок п. В результате получают точ­ку 1₀. Так же находят и новые горизонтальные про­екции точек 2-5. Соединив прямыми линиями новые горизонтальные проекции 1₀-5₀, получают действительный вид фигуры сечения.

Разверткой называется плоская фигура, получен­ная при совмещении поверхности геометрического тела с одной плоскостью (без наложения граней или иных элементов поверхности друг на друга).

Развертку боковой поверхности с основанием и фигурой сечения призмы строят следующим образом. Проводят прямую, на которой отклады­вают пять отрезков, равных длинам сторон пятиу­гольника, лежащего в основании призмы. Из полу­ченных точек проводят перпендикуляры, на ко­торых откладывают действительные длины ребер усеченной призмы, беря их с фронтальной или про­фильной проекций (рис. 15,б).

К развертке боковой поверхности пристраивают фигуру нижнего основания–пятиугольник и фигуру сечения. При этом используют метод триангуляции или метод координат, известный из геометрического черчения. На рис. 15, а и б показано построение вершины 5 методом триангуляции. Линии сгиба по ГОСТ 2.303-68 показывают на развертке штрихпунктирной линией с двумя точками.

Для наглядности полезно выполнить построение усеченного тела в аксонометрической проекции. На рис. 173, в построена изометрическая проекция усеченной призмы. Порядок построения изометрической проекции следующий. Строят изометрическую проекцию основания призмы; проводят в вертикальном направлении линии ребер, на которых от основания откладывают их действительные длины, взятые с фронтальной или профильной проекции призмы. Полученные точки 1'-5' соединяют прямыми линиями.