
- •1.1. Двойной интеграл
- •2. Геометрический и физический смысл двойного интеграла. Основные свойства двойного интеграла.
- •4 Вычисление двойного интеграла в полярных координатах
- •5 Приложения двойного интеграла Объем тела
- •Площадь плоской фигуры
- •6 Тройной интеграл
- •1) Разбиваем область на «элементарных областей» .
- •3) Возьмем произвольную точку .
- •5) Составляем интегральную сумму
- •Основные свойства тройного интеграла
- •7 Замена переменной в тройном интеграле. Вычисление тройного интеграла в цилиндрических и сферических координатах.
- •8. Некоторые приложения тройного интеграла в геометрии и физике
- •9. Криволинейный интеграл I рода. Основные свойства кри-I.
- •Основные свойства кри-I
- •10. Вычисление криволинейного интеграла I рода: явное представление кривой, параметрическое представление кривой, полярное представление кривой.
- •2.2. Вычисления криволинейного интеграла I рода
- •11. Некоторые приложения кри-I рода в геометрии и физике.
- •Площадь цилиндрической поверхности
- •12. Криволинейный интеграл II рода. Основные свойства кри-II.
- •Криволинейный интеграл II рода (кри-II)
- •Основные свойства кри-II
- •13. Вычисление кри-II: явное представление кривой, параметрическое представление кривой. Некоторые приложения кри-II.
- •2.5. Вычисления криволинейного интеграла II рода
- •Явное представление кривой
- •Параметрическое представление кривой
- •2.6. Некоторые приложения криволинейного интеграла II рода Площадь плоской фигуры
- •Работа переменной силы
- •14. Формула Остроградского – Грина.
- •15.Поверхностный интеграл I рода. Основные свойства поверхностного интеграла I рода. Вычисление поверхностного интеграла I рода.
- •3.2. Вычисление поверхностного интеграла I рода
- •16.Поверхностный интеграл II рода. Свойства поверхностного интеграла II рода.
- •3.3. Поверхностный интеграл II рода
- •17.Вычисление поверхностного интеграла II рода. Формула Остроградского - Гаусса для вычисления поверхностного интеграла II рода.
- •3.4. Вычисление поверхностного интеграла II рода
- •I способ
- •II способ
- •II способ
- •III способ
- •18. Скалярное поле. Поверхность и линии уровня. Производная по направлению. Градиент.
- •Производная по направлению
- •Градиент
- •19.Векторное поле. Векторные (силовые) линии. Векторная трубка.
- •20. Поток векторного поля через поверхность. Формула вычисления потока векторного поля. Источник и сток. Формула Остроградского – Гаусса для вычисления потока.
- •4.3. Поток векторного поля через поверхность
- •21.Дивергенция поля. Некоторые свойства дивергенции. Физический смысл дивергенции.
- •22. Циркуляция поля. Физический смысл циркуляции поля.
- •4.5. Циркуляция поля
- •23. Ротор поля. Некоторые свойства ротора. Формула Стокса.
- •4.6. Ротор поля. Формула Стокса
- •24. Векторные дифференциальные операции первого порядка.
- •Векторные дифференциальные операции первого и второго порядка
- •25. Векторные дифференциальные операции второго порядка.
- •26.Классификация векторных полей: определения соленоидального, потенциального и гармонического векторного поля.
- •4.8. Классификация векторных полей Соленоидальное векторное поле
- •Потенциальное векторное поле
- •Гармоническое векторное поле
- •27.Числовой ряд. -ая частичная сумма ряда. Сходимость и расходимость ряда. Некоторые свойства рядов. -ый остаток ряда.
- •5.1. Основные понятия
- •28. Сформулировать и доказать необходимый признак сходимости ряда. Достаточный признак расходимости ряда. Гармонический ряд.
- •5.2. Необходимый признак сходимости ряда
- •5.3. Достаточные признаки сходимости ряда
- •29. Признаки сравнения рядов. Признак Даламбера Признаки сравнения рядов.
- •Признак Даламбера
- •30. Радикальный признак Коши. Интегральный признак Коши. Ряд Дирихле.
- •Интегральный признак Коши
- •31. Знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимости рядов.
- •6.1. Знакочередующиеся ряды. Признак Лейбница
- •Абсолютная и условная сходимости рядов
- •32. Функциональный ряд. Точка сходимости. Область сходимости функциональног
- •7.1. Функциональные ряды
- •33. Степенной ряд. Сформулировать и доказать теорему Абеля.
- •34. Интервал и радиус сходимости степенного ряда. Интервал и радиус сходимости
- •Свойства степенных рядов
- •35. Ряды Тейлора и Маклорена. Разложение функций в степенной ряд.
- •Разложение функций в степенной ряд
- •36. Некоторые приложения степенных рядов.
- •Некоторые приложения степенных рядов
- •Вычисление значений функции
- •2. Вычисление интегралов
- •3. Приближенное решение дифференциальных уравнений
- •Способ последовательного дифференцирования
- •Способ неопределенных коэффициентов
- •37. Тригонометрический ряд. Формулы коэффициентов ряда Фурье
- •8.1. Периодические функции. Периодические процессы
- •Тригонометрический ряд Фурье
- •38.Разложение в ряд Фурье -периодических функций. Теорема Дирихле. Разложение в ряд Фурье четных и нечетных функций.
- •8.3. Разложение в ряд Фурье -периодических функций
- •8.4. Разложение в ряд Фурье четных и нечетных функций
- •39. Разложение в ряд Фурье функций произвольного периода.
- •40Уравнение колебаний струны.
- •Уравнение колебаний струны
- •Уравнение теплопроводности.
15.Поверхностный интеграл I рода. Основные свойства поверхностного интеграла I рода. Вычисление поверхностного интеграла I рода.
п. 3. Поверхностные интегралы
Обобщением двойного интеграла является так называемый поверхностный интеграл.
3.1. Поверхностный интеграл I рода
Пусть в точках некоторой гладкой поверхности пространства определена непрерывная функция .

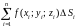 .
.
Если при
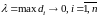 и
интегральная сумма
имеет предел, то он называется поверхностным
интегралом I
рода от функции
по поверхности
и обозначается
и
интегральная сумма
имеет предел, то он называется поверхностным
интегралом I
рода от функции
по поверхности
и обозначается
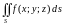 .
.
Таким образом, по определению,
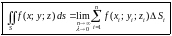 .
(3.1)
.
(3.1)
Основные свойства поверхностного интеграла I рода
1.
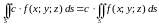 ,
где
.
,
где
.
2.
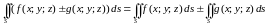 .
.
3. Если поверхность
разбить на части
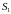 и
и
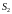 такие, что
такие, что
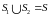 ,
а пересечение
и
состоит лишь из границы, их разделяющей,
то
,
а пересечение
и
состоит лишь из границы, их разделяющей,
то
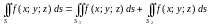 .
.
4. Если на поверхности
функции
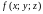 и
и
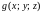 удовлетворяют неравенству
удовлетворяют неравенству
 ,
то и
,
то и
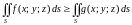 .
.
5. Если
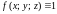 ,
то
,
то
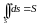 ,
где
площадь поверхности
.
,
где
площадь поверхности
.
6. (Теорема о среднем) Если функция
непрерывна на поверхности
,
то на этой поверхности существует такая
точка
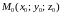 ,
что
,
что
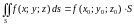 .
.
3.2. Вычисление поверхностного интеграла I рода
Вычисление поверхностного интеграла I рода сводится к вычислению двойного интеграла по области проекции поверхности на плоскости .
Если поверхность
задана уравнением
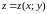 ,
то поверхностный интеграл I
рода вычисляется по следующей формуле:
,
то поверхностный интеграл I
рода вычисляется по следующей формуле:
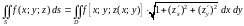 ,
(3.2)
,
(3.2)
где проекция поверхности на координатную плоскость .
Если поверхность
задана уравнениями вида
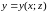 или
или
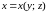 ,
то получаем следующие формулы
,
то получаем следующие формулы
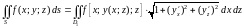
и
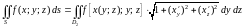 ,
,
где
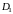 и
и
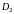 проекции поверхности
на координатную плоскость
проекции поверхности
на координатную плоскость
 и
и
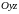 соответственно.
соответственно.
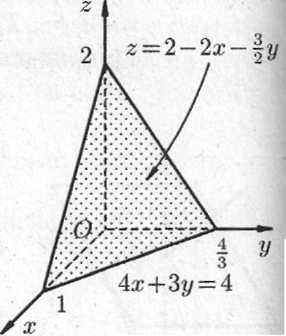
Пример 3.1. Вычислить
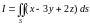 ,
где
часть плоскости
,
где
часть плоскости
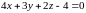 ,
расположенной в первом октанте.
,
расположенной в первом октанте.
Решение. Построим плоскость в пространстве (см. рисунок).
Запишем уравнение плоскости в виде
 .
Находим
.
Находим
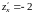 ,
,
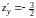 .
.
По формуле (3.2) имеем:
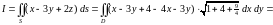
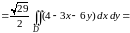
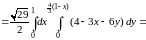
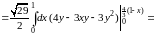
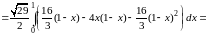
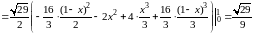 .
.
,
Пример 3.2. Вычислить
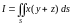 ,
где
часть цилиндрической
поверхности
,
где
часть цилиндрической
поверхности ,
отсеченной плоскостями
,
отсеченной плоскостями
 .
.
Решение. В пространстве строим поверхность .
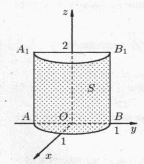
Поскольку
 ,
,
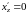 ,
то получаем
,
то получаем
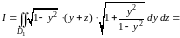
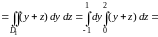
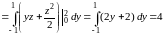 ,
,
где
прямоугольник
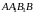 .
.
16.Поверхностный интеграл II рода. Свойства поверхностного интеграла II рода.
3.3. Поверхностный интеграл II рода
Пусть задана гладкая поверхность
.
Сторона поверхности
,
в каждой точки которой построен вектор
нормали
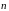 ,
называется положительной, а
другая ее сторона (если она существует)
– отрицательной. Если, в частности,
поверхность
является замкнутой и ограничивает
некоторую область пространства
,
то положительной или внешней стороной
поверхности называется та ее
сторона, нормальные векторы которой
направлены от области
,
а отрицательной или внутренней
– сторона, нормальные векторы которой
направлены в область
.
,
называется положительной, а
другая ее сторона (если она существует)
– отрицательной. Если, в частности,
поверхность
является замкнутой и ограничивает
некоторую область пространства
,
то положительной или внешней стороной
поверхности называется та ее
сторона, нормальные векторы которой
направлены от области
,
а отрицательной или внутренней
– сторона, нормальные векторы которой
направлены в область
.
Поверхность, у которой существует положительная (внешняя) и отрицательная (внутренняя) стороны, называется двухсторонней. Примерами двухсторонних поверхностей являются плоскость, поверхности второго порядка, тор и др. Двухсторонняя поверхность характеризуется следующим свойством: если основание вектора нормали непрерывно перемещать по любому замкнутому контуру , лежащему на такой поверхности, то при возвращении в исходную точку направление совпадает с исходным.
Для односторонних поверхностей указанное
перемещение нормали
при возвращении в исходную точку приводит
к «антинормали», т.е. к вектору
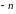 .
Классическим примером односторонней
поверхности является лист Мебиуса.
.
Классическим примером односторонней
поверхности является лист Мебиуса.
Поверхность с выбранной стороной называется ориентированной.
Пусть в прямоугольной системе координат задана некоторая область . И пусть в этой области задана поверхность , ограниченная некоторой пространственной линией .
Относительно поверхности
будем предполагать, что в каждой ее
точке
определяется положительное направление
нормали единичным вектором
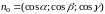 ,
направляющие косинусы которого являются
непрерывными функциями координат точек
поверхности.
,
направляющие косинусы которого являются
непрерывными функциями координат точек
поверхности.
Если поверхность
задана уравнением
,
то нормальный вектор
,
образующий с осью
острый угол
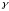 ,
определяется следующим образом:
,
определяется следующим образом:
 ,
тогда координаты единичного вектора
нормали
,
тогда координаты единичного вектора
нормали
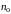 :
:
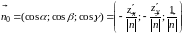 .
.
Если поверхность
задана уравнением
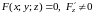 ,
то
,
то
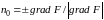 ,
,
где знак «+» берется в случае, когда угол острый, а знак «» в случае, когда тупой.
Пусть в области пространства определена вектор-функция
,
где
 функции непрерывные
в области
.
функции непрерывные
в области
.
Разобьем поверхность
на элементарные площадки
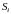 ,
площадки которых
,
площадки которых
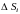 ,
а диаметры – через
,
а диаметры – через
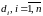 .
На каждой площадке
выберем произвольную точку
.
На каждой площадке
выберем произвольную точку
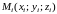 .
Найдем интегральную сумму
.
Найдем интегральную сумму
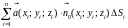 .
.
Предел интегральной суммы, найденный
при условии, что
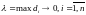 ,
,
называется поверхностным интегралом
второго рода от вектор-функции
по поверхности
и обозначается
,
,
называется поверхностным интегралом
второго рода от вектор-функции
по поверхности
и обозначается
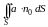 .
.
Таким образом, по определению
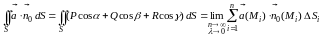 .
.
(3.3)
Надо отметить, что если поверхность такова, что в каждой ее точке существует касательная плоскость, которая непрерывно меняется с перемещением точки по поверхности, и если вектор-функция непрерывна на этой поверхности, то этот предел существует.
Произведение
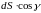 есть проекция площадки
на плоскость
,
то
есть проекция площадки
на плоскость
,
то
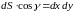 .
Аналогично получаем:
.
Аналогично получаем:
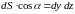 ,
,
 .
Тогда формулу (3.3) можно записать в виде
.
Тогда формулу (3.3) можно записать в виде
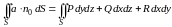 .
(3.4)
.
(3.4)
Каждое слагаемое интегральной суммы
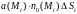 может
быть истолковано механически следующим
образом: это произведение равно объему
цилиндра с основанием
и высотой
может
быть истолковано механически следующим
образом: это произведение равно объему
цилиндра с основанием
и высотой
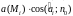 .
Если вектор
есть скорость жидкости, протекающей
через поверхность
,
то произведение
.
Если вектор
есть скорость жидкости, протекающей
через поверхность
,
то произведение
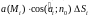 равно количеству жидкости, протекающей
через площадку
за единицу времени в направлении вектора
.
равно количеству жидкости, протекающей
через площадку
за единицу времени в направлении вектора
.
Выражение
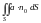 представляет собой общее количество
жидкости, протекающей в единицу времени
через поверхность
в положительном направлении, если под
вектором
подразумевать вектор скорости течения
жидкости в данной точке. Поэтому
поверхностный интеграл второго рода
называется потоком векторного поля
через поверхность
.
представляет собой общее количество
жидкости, протекающей в единицу времени
через поверхность
в положительном направлении, если под
вектором
подразумевать вектор скорости течения
жидкости в данной точке. Поэтому
поверхностный интеграл второго рода
называется потоком векторного поля
через поверхность
.
Отметим, что если
замкнутая поверхность,
то поверхностный интеграл по внешней
стороне ее обозначается
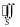 ,
по внутренней
,
по внутренней
 .
.
свойства
Поверхностный интеграл II рода изменяет знак при перемене стороны поверхности.
Постоянный множитель можно вынести за знак поверхностного интеграла.
Поверхностный интеграл от суммы функций равен сумме соответствующих интегралов от слагаемых.
Поверхностный интеграл II рода по всей поверхности
 равен сумме интегралов по ее частям
равен сумме интегралов по ее частям
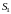 и
и
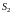 (аддитивное свойство), если
и
пересекаются лишь по границе, их
разделяющей.
(аддитивное свойство), если
и
пересекаются лишь по границе, их
разделяющей.Если , и
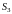 цилиндрические
поверхности с образующими, параллельными
соответственно осям
цилиндрические
поверхности с образующими, параллельными
соответственно осям
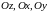 ,
то
,
то
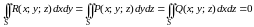 .
.
