
- •1.1. Двойной интеграл
- •2. Геометрический и физический смысл двойного интеграла. Основные свойства двойного интеграла.
- •4 Вычисление двойного интеграла в полярных координатах
- •5 Приложения двойного интеграла Объем тела
- •Площадь плоской фигуры
- •6 Тройной интеграл
- •1) Разбиваем область на «элементарных областей» .
- •3) Возьмем произвольную точку .
- •5) Составляем интегральную сумму
- •Основные свойства тройного интеграла
- •7 Замена переменной в тройном интеграле. Вычисление тройного интеграла в цилиндрических и сферических координатах.
- •8. Некоторые приложения тройного интеграла в геометрии и физике
- •9. Криволинейный интеграл I рода. Основные свойства кри-I.
- •Основные свойства кри-I
- •10. Вычисление криволинейного интеграла I рода: явное представление кривой, параметрическое представление кривой, полярное представление кривой.
- •2.2. Вычисления криволинейного интеграла I рода
- •11. Некоторые приложения кри-I рода в геометрии и физике.
- •Площадь цилиндрической поверхности
- •12. Криволинейный интеграл II рода. Основные свойства кри-II.
- •Криволинейный интеграл II рода (кри-II)
- •Основные свойства кри-II
- •13. Вычисление кри-II: явное представление кривой, параметрическое представление кривой. Некоторые приложения кри-II.
- •2.5. Вычисления криволинейного интеграла II рода
- •Явное представление кривой
- •Параметрическое представление кривой
- •2.6. Некоторые приложения криволинейного интеграла II рода Площадь плоской фигуры
- •Работа переменной силы
- •14. Формула Остроградского – Грина.
- •15.Поверхностный интеграл I рода. Основные свойства поверхностного интеграла I рода. Вычисление поверхностного интеграла I рода.
- •3.2. Вычисление поверхностного интеграла I рода
- •16.Поверхностный интеграл II рода. Свойства поверхностного интеграла II рода.
- •3.3. Поверхностный интеграл II рода
- •17.Вычисление поверхностного интеграла II рода. Формула Остроградского - Гаусса для вычисления поверхностного интеграла II рода.
- •3.4. Вычисление поверхностного интеграла II рода
- •I способ
- •II способ
- •II способ
- •III способ
- •18. Скалярное поле. Поверхность и линии уровня. Производная по направлению. Градиент.
- •Производная по направлению
- •Градиент
- •19.Векторное поле. Векторные (силовые) линии. Векторная трубка.
- •20. Поток векторного поля через поверхность. Формула вычисления потока векторного поля. Источник и сток. Формула Остроградского – Гаусса для вычисления потока.
- •4.3. Поток векторного поля через поверхность
- •21.Дивергенция поля. Некоторые свойства дивергенции. Физический смысл дивергенции.
- •22. Циркуляция поля. Физический смысл циркуляции поля.
- •4.5. Циркуляция поля
- •23. Ротор поля. Некоторые свойства ротора. Формула Стокса.
- •4.6. Ротор поля. Формула Стокса
- •24. Векторные дифференциальные операции первого порядка.
- •Векторные дифференциальные операции первого и второго порядка
- •25. Векторные дифференциальные операции второго порядка.
- •26.Классификация векторных полей: определения соленоидального, потенциального и гармонического векторного поля.
- •4.8. Классификация векторных полей Соленоидальное векторное поле
- •Потенциальное векторное поле
- •Гармоническое векторное поле
- •27.Числовой ряд. -ая частичная сумма ряда. Сходимость и расходимость ряда. Некоторые свойства рядов. -ый остаток ряда.
- •5.1. Основные понятия
- •28. Сформулировать и доказать необходимый признак сходимости ряда. Достаточный признак расходимости ряда. Гармонический ряд.
- •5.2. Необходимый признак сходимости ряда
- •5.3. Достаточные признаки сходимости ряда
- •29. Признаки сравнения рядов. Признак Даламбера Признаки сравнения рядов.
- •Признак Даламбера
- •30. Радикальный признак Коши. Интегральный признак Коши. Ряд Дирихле.
- •Интегральный признак Коши
- •31. Знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимости рядов.
- •6.1. Знакочередующиеся ряды. Признак Лейбница
- •Абсолютная и условная сходимости рядов
- •32. Функциональный ряд. Точка сходимости. Область сходимости функциональног
- •7.1. Функциональные ряды
- •33. Степенной ряд. Сформулировать и доказать теорему Абеля.
- •34. Интервал и радиус сходимости степенного ряда. Интервал и радиус сходимости
- •Свойства степенных рядов
- •35. Ряды Тейлора и Маклорена. Разложение функций в степенной ряд.
- •Разложение функций в степенной ряд
- •36. Некоторые приложения степенных рядов.
- •Некоторые приложения степенных рядов
- •Вычисление значений функции
- •2. Вычисление интегралов
- •3. Приближенное решение дифференциальных уравнений
- •Способ последовательного дифференцирования
- •Способ неопределенных коэффициентов
- •37. Тригонометрический ряд. Формулы коэффициентов ряда Фурье
- •8.1. Периодические функции. Периодические процессы
- •Тригонометрический ряд Фурье
- •38.Разложение в ряд Фурье -периодических функций. Теорема Дирихле. Разложение в ряд Фурье четных и нечетных функций.
- •8.3. Разложение в ряд Фурье -периодических функций
- •8.4. Разложение в ряд Фурье четных и нечетных функций
- •39. Разложение в ряд Фурье функций произвольного периода.
- •40Уравнение колебаний струны.
- •Уравнение колебаний струны
- •Уравнение теплопроводности.
11. Некоторые приложения кри-I рода в геометрии и физике.
Некоторые приложения криволинейного интеграла I рода
Криволинейный интеграл I рода имеет разнообразные приложения в математике и механике.
Длина кривой
Длина
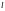 кривой
,
плоской или пространственной линии,
вычисляется по следующей формуле
кривой
,
плоской или пространственной линии,
вычисляется по следующей формуле
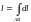 .
.
Площадь цилиндрической поверхности
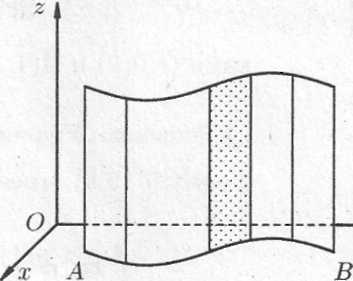
Если направляющей
цилиндрической поверхности служит
кривая
,
лежащая в плоскости
,
а образующая параллельная оси
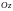 (см. рисунок), то площадь поверхности,
заданной функцией
(см. рисунок), то площадь поверхности,
заданной функцией
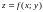 ,
находится по формуле:
,
находится по формуле:
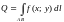
Масса кривой
Если
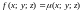
плотность материальной кривой
(провод, цепь, трос, …), то ее масса
вычисляется по формуле:
плотность материальной кривой
(провод, цепь, трос, …), то ее масса
вычисляется по формуле:
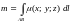 .
.
Координаты центра масс
Координаты центра
масс материальной дуги
,
имеющей плотность
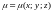 ,
определяются по формулам:
,
определяются по формулам:
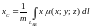 ;
;
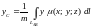 ;
;
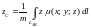 .
.
Моменты инерции
Моменты инерции
относительно начала координат
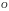 ,
осей координат
,
осей координат
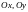 и
,
и координатных плоскостей
и
,
и координатных плоскостей
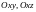 и
и
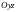 материальной дуги
,
имеющей плотность
,
определяются по формулам:
материальной дуги
,
имеющей плотность
,
определяются по формулам:
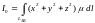 ;
;
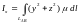 ,
,
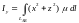 ,
,
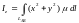 ;
;
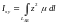 ,
,
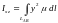 ,
,
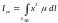 .
.
Пример 2.3.
Вычислить массу и координаты центра
масс плоской материальной дуги
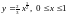 ,
плотность которой
,
плотность которой
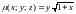 .
.
Решение. Согласно формуле (2.3) и формуле массы кривой, для случая плоской дуги имеем:
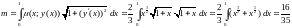 .
.
Согласно формулам координат центра масс, получаем:

 .
.
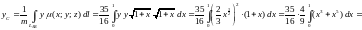
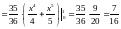 .
.
12. Криволинейный интеграл II рода. Основные свойства кри-II.
Криволинейный интеграл II рода (кри-II)
Решение задачи о вычислении работы переменной силы при перемещении материальной точки вдоль некоторой кривой приводит к понятию криволинейного интеграла второго рода. Криволинейный интеграл II рода определяется так же, как и интеграл I.
Пусть в пространстве ( ) задан вектор
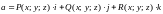 ,
,
координаты которого – непрерывные функции в точках ориентированной кривой .
Кривую
разобьем в направлении от
к
на
 элементарных дуг
элементарных дуг
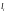 и построим векторы
и построим векторы
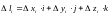 ,
где
,
где
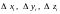
проекции векторов
проекции векторов
 на оси координат.
на оси координат.
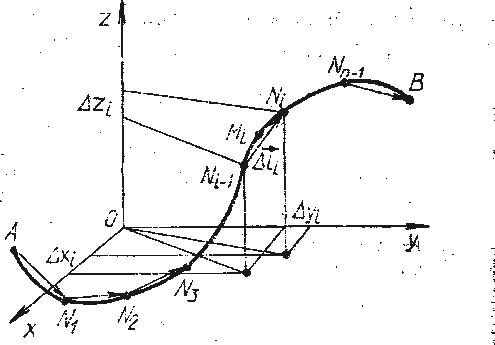
Начала этих векторов
совпадают с началом элементарных дуг
,
а концы – с их концами. На каждой
элементарной части
выберем произвольную точку
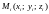 и составим интегральную сумму
и составим интегральную сумму
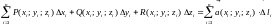 .
.
Предел интегральной
суммы, найденный при условии, что
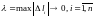 ,
и не зависящий ни от способа разбиения
кривой
,
ни от выбора произвольной точки
,
называется криволинейным
интегралом второго рода
(КРИ-II)
или криволинейным
интегралом
по координатам от вектор-функции
,
и не зависящий ни от способа разбиения
кривой
,
ни от выбора произвольной точки
,
называется криволинейным
интегралом второго рода
(КРИ-II)
или криволинейным
интегралом
по координатам от вектор-функции
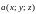 по кривой
.
Обозначается:
по кривой
.
Обозначается:
 .
.
(2.6)
Если функции
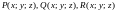
непрерывны в точках гладкой кривой
,
то предел интегральной суммы существует,
т.е. существует криволинейный интеграл
второго рода.
непрерывны в точках гладкой кривой
,
то предел интегральной суммы существует,
т.е. существует криволинейный интеграл
второго рода.
Основные свойства кри-II
1. При изменении направления пути интегрирования криволинейный интеграл II рода изменяет свой знак на противоположный, т.е.
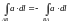 .
.
2. Если кривая
точкой
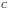 разбита на две части
разбита на две части
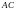 и
и
 ,
то интеграл по всей кривой равен сумме
интегралов по ее частям, т.е.
,
то интеграл по всей кривой равен сумме
интегралов по ее частям, т.е.
 .
.
Если кривая
интегрирования замкнута, криволинейный
интеграл II
рода обозначается
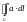 .
В этом случае через кривую
проводится ориентированная поверхность
и за положительное направление обхода
по
принимается такое направление, при
котором область поверхности, ограниченная
кривой
,
находится слева, если двигаться вдоль
по выбранной стороне указанной
поверхности, т.е. за
положительный обход контура
принимается
обход против хода часовой стрелки.
.
В этом случае через кривую
проводится ориентированная поверхность
и за положительное направление обхода
по
принимается такое направление, при
котором область поверхности, ограниченная
кривой
,
находится слева, если двигаться вдоль
по выбранной стороне указанной
поверхности, т.е. за
положительный обход контура
принимается
обход против хода часовой стрелки.
Если плоскую
область
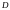 ,
ограниченную кривой
,
разбить на части, не имеющие общих
внутренних точек и ограниченные
замкнутыми кривыми
и
,
то
,
ограниченную кривой
,
разбить на части, не имеющие общих
внутренних точек и ограниченные
замкнутыми кривыми
и
,
то
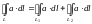 ,
,
где направления обхода по контурам , и всюду либо положительные, либо отрицательные.
