38.Разложение в ряд Фурье -периодических функций. Теорема Дирихле. Разложение в ряд Фурье четных и нечетных функций.

8.3. Разложение в ряд Фурье -периодических функций

Выясним условия, при которых ряд Фурье функции сходится и имеет своей суммой как раз функцию .

Будем рассматривать функции , имеющие период . Такие функции называются периодическими.

Сформулируем теорему (без доказательства), представляющую достаточное условие разложимости функции в ряд Фурье.

Теорема 8.1 (теорема Дирихле). Пусть периодическая функция на отрезке удовлетворяет двум условиям:

1. кусочно-непрерывна, т.е. непрерывна или имеет конечное число точек разрыва I рода;

2. кусочно-монотонна, т.е. монотонная на всем отрезке, либо этот отрезок можно разбить на конечное число интервалов так, что на каждом из них функция монотонна.

Тогда соответствующей функции ряд Фурье сходится на этом отрезке и при этом:

1. в точках непрерывности функции сумма ряда совпадает с самой функцией , т.е. ;

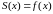2. в каждой точке разрыва функции сумма ряда равна среднему арифметическому пределов функции справа и слева, т.е.

;

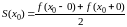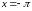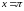3. в точках и (на концах отрезка) сумма ряда равна

.

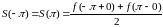Таким образом, если функция удовлетворяет условиям 1 и 2 теоремы Дирихле, то на отрезке имеет место разложение (8.4), причем коэффициенты вычисляются по формулам (8.5)  (8.7). Это равенство может нарушиться только в точках разрыва функции и на концах отрезка .

В силу периодичности функции и суммы ряда Фурье может быть получено указанное разложение во всей области определения функции.

Если функция с периодом на отрезке удовлетворяет условиям теоремы Дирихле, то для нее имеет место разложение (8.4), где коэффициенты вычисляются по формулам (8.5)  (8.7).

Надо отметить, что условиям теоремы Дирихле удовлетворяют большинство функций, встречающихся в математике и ее приложениях. Существуют функции, не удовлетворяющие условиям теоремы Дирихле, но при этом их можно разложить в ряд Фурье, т.е. теорема Дирихле дает лишь достаточное условие разложимости, но не необходимое.

8.4. Разложение в ряд Фурье четных и нечетных функций

Если разлагаемая на отрезке в ряд Фурье функция является четной или нечетной, то это отражается на формулах коэффициентов Фурье (вычисление их упрощается) и на виде самого ряда (он становится так называемым неполным).

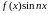Допустим, что разлагаемая в ряд Фурье функция  четная. Тогда функции будут нечетными и все коэффициенты , как интегралы от нечетных функций по интервалу , симметричному относительно начала координат, окажутся равными нулю. Функции 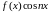будут четными.

Итак, если функция  четная, то ряд Фурье имеет вид (состоит из одних косинусов):

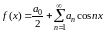, (8.8)

где , , .

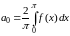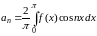Допустим, что разлагаемая в ряд Фурье функция  нечетная. Тогда функции будут нечетными и все коэффициенты , как интегралы от нечетных функций по интервалу , симметричному относительно начала координат, окажутся равными нулю. Функции будут четными.

Итак, если функция  нечетная, то ряд Фурье имеет вид (состоит из одних синусов):

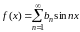, (8.9)

где , .

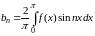Ряды (8.8) и (8.9) называются неполными тригонометрическими рядами, или рядами по косинусам и по синусам соответственно.