
- •1.1. Двойной интеграл
- •2. Геометрический и физический смысл двойного интеграла. Основные свойства двойного интеграла.
- •4 Вычисление двойного интеграла в полярных координатах
- •5 Приложения двойного интеграла Объем тела
- •Площадь плоской фигуры
- •6 Тройной интеграл
- •1) Разбиваем область на «элементарных областей» .
- •3) Возьмем произвольную точку .
- •5) Составляем интегральную сумму
- •Основные свойства тройного интеграла
- •7 Замена переменной в тройном интеграле. Вычисление тройного интеграла в цилиндрических и сферических координатах.
- •8. Некоторые приложения тройного интеграла в геометрии и физике
- •9. Криволинейный интеграл I рода. Основные свойства кри-I.
- •Основные свойства кри-I
- •10. Вычисление криволинейного интеграла I рода: явное представление кривой, параметрическое представление кривой, полярное представление кривой.
- •2.2. Вычисления криволинейного интеграла I рода
- •11. Некоторые приложения кри-I рода в геометрии и физике.
- •Площадь цилиндрической поверхности
- •12. Криволинейный интеграл II рода. Основные свойства кри-II.
- •Криволинейный интеграл II рода (кри-II)
- •Основные свойства кри-II
- •13. Вычисление кри-II: явное представление кривой, параметрическое представление кривой. Некоторые приложения кри-II.
- •2.5. Вычисления криволинейного интеграла II рода
- •Явное представление кривой
- •Параметрическое представление кривой
- •2.6. Некоторые приложения криволинейного интеграла II рода Площадь плоской фигуры
- •Работа переменной силы
- •14. Формула Остроградского – Грина.
- •15.Поверхностный интеграл I рода. Основные свойства поверхностного интеграла I рода. Вычисление поверхностного интеграла I рода.
- •3.2. Вычисление поверхностного интеграла I рода
- •16.Поверхностный интеграл II рода. Свойства поверхностного интеграла II рода.
- •3.3. Поверхностный интеграл II рода
- •17.Вычисление поверхностного интеграла II рода. Формула Остроградского - Гаусса для вычисления поверхностного интеграла II рода.
- •3.4. Вычисление поверхностного интеграла II рода
- •I способ
- •II способ
- •II способ
- •III способ
- •18. Скалярное поле. Поверхность и линии уровня. Производная по направлению. Градиент.
- •Производная по направлению
- •Градиент
- •19.Векторное поле. Векторные (силовые) линии. Векторная трубка.
- •20. Поток векторного поля через поверхность. Формула вычисления потока векторного поля. Источник и сток. Формула Остроградского – Гаусса для вычисления потока.
- •4.3. Поток векторного поля через поверхность
- •21.Дивергенция поля. Некоторые свойства дивергенции. Физический смысл дивергенции.
- •22. Циркуляция поля. Физический смысл циркуляции поля.
- •4.5. Циркуляция поля
- •23. Ротор поля. Некоторые свойства ротора. Формула Стокса.
- •4.6. Ротор поля. Формула Стокса
- •24. Векторные дифференциальные операции первого порядка.
- •Векторные дифференциальные операции первого и второго порядка
- •25. Векторные дифференциальные операции второго порядка.
- •26.Классификация векторных полей: определения соленоидального, потенциального и гармонического векторного поля.
- •4.8. Классификация векторных полей Соленоидальное векторное поле
- •Потенциальное векторное поле
- •Гармоническое векторное поле
- •27.Числовой ряд. -ая частичная сумма ряда. Сходимость и расходимость ряда. Некоторые свойства рядов. -ый остаток ряда.
- •5.1. Основные понятия
- •28. Сформулировать и доказать необходимый признак сходимости ряда. Достаточный признак расходимости ряда. Гармонический ряд.
- •5.2. Необходимый признак сходимости ряда
- •5.3. Достаточные признаки сходимости ряда
- •29. Признаки сравнения рядов. Признак Даламбера Признаки сравнения рядов.
- •Признак Даламбера
- •30. Радикальный признак Коши. Интегральный признак Коши. Ряд Дирихле.
- •Интегральный признак Коши
- •31. Знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимости рядов.
- •6.1. Знакочередующиеся ряды. Признак Лейбница
- •Абсолютная и условная сходимости рядов
- •32. Функциональный ряд. Точка сходимости. Область сходимости функциональног
- •7.1. Функциональные ряды
- •33. Степенной ряд. Сформулировать и доказать теорему Абеля.
- •34. Интервал и радиус сходимости степенного ряда. Интервал и радиус сходимости
- •Свойства степенных рядов
- •35. Ряды Тейлора и Маклорена. Разложение функций в степенной ряд.
- •Разложение функций в степенной ряд
- •36. Некоторые приложения степенных рядов.
- •Некоторые приложения степенных рядов
- •Вычисление значений функции
- •2. Вычисление интегралов
- •3. Приближенное решение дифференциальных уравнений
- •Способ последовательного дифференцирования
- •Способ неопределенных коэффициентов
- •37. Тригонометрический ряд. Формулы коэффициентов ряда Фурье
- •8.1. Периодические функции. Периодические процессы
- •Тригонометрический ряд Фурье
- •38.Разложение в ряд Фурье -периодических функций. Теорема Дирихле. Разложение в ряд Фурье четных и нечетных функций.
- •8.3. Разложение в ряд Фурье -периодических функций
- •8.4. Разложение в ряд Фурье четных и нечетных функций
- •39. Разложение в ряд Фурье функций произвольного периода.
- •40Уравнение колебаний струны.
- •Уравнение колебаний струны
- •Уравнение теплопроводности.
36. Некоторые приложения степенных рядов.
Некоторые приложения степенных рядов
Вычисление значений функции
Пусть дан степенной ряд функции
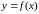 .
Задача вычисления значения этой функции
заключается в отыскании суммы ряда при
заданном значении аргумента. Ограничиваясь
определенным числом членов ряда, находим
значение функции с точностью, которую
можно устанавливать путем оценивания
остатка числового ряда либо остаточного
члена
формул Тейлора или Маклорена.
.
Задача вычисления значения этой функции
заключается в отыскании суммы ряда при
заданном значении аргумента. Ограничиваясь
определенным числом членов ряда, находим
значение функции с точностью, которую
можно устанавливать путем оценивания
остатка числового ряда либо остаточного
члена
формул Тейлора или Маклорена.
2. Вычисление интегралов
Так как степенные ряды сходятся равномерно на любом отрезке, лежащем внутри интервалов сходимости, то с помощью разложений функций в степенные ряды можно находить неопределенные интегралы в виде степенных рядов и приближенно вычислять соответствующие определенные интегралы.
Пример 7.11. Вычислить
 с точностью
.
с точностью
.
Решение. Воспользуемся формулой
разложения функции
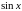 в степенной ряд, заменив
на
в степенной ряд, заменив
на
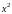 .
Получаем ряд
.
Получаем ряд
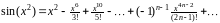 .
.
Полученный ряд сходится на всей числовой прямой, поэтому его можно всюду почленно интегрировать. Следовательно,
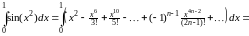
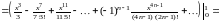
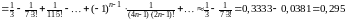 ,
,
Поскольку уже третий член полученного знакочередующегося ряда меньше .
3. Приближенное решение дифференциальных уравнений
Если решение дифференциального уравнения не выражается через элементарные функции в конечном виде или способ его решения слишком сложен, то для приближенного решения можно воспользоваться рядом Тейлора.
Рассмотрим два способа решения дифференциальных уравнений с помощью степенных рядов.
Способ последовательного дифференцирования
При решении задачи Коши
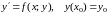 ,
,
используется ряд Тейлора
 ,
,
где
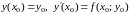 ,
а остальные производные
,
а остальные производные
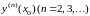 находятся путем последовательного
дифференцирования уравнения
находятся путем последовательного
дифференцирования уравнения
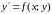 и подстановки начальных данных в
выражения для этих производных.
и подстановки начальных данных в
выражения для этих производных.
Надо отметить, что способ последовательного дифференцирования применим для решения дифференциальных уравнений любого порядка.
Пример 7.12. Найти пять первых членов (отличных от нуля) разложения в степенной ряд решения дифференциального уравнения
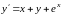 ,
если
,
если
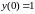 .
.
Решение. Находим решение дифференциального уравнения (при ) в виде
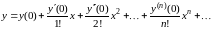 .
.
.
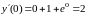 .
.
Далее находим производные высших порядков и значения производных при .
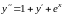 .
Тогда
.
Тогда
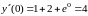 .
.
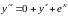 .
Тогда
.
Тогда
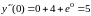 .
.
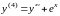 .
Тогда
.
Тогда
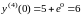 .
.
Подставляя найденные значения производных в искомый ряд, получаем:
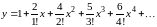 .
.
Способ неопределенных коэффициентов
Этот способ приближенного решения наиболее удобен для линейных дифференциальных уравнений с переменными коэффициентами.
Пусть, например, требуется решить уравнение
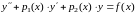
с
начальными условиями
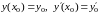 .
.
Предполагая, что коэффициенты
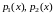 и свободный член
разлагаются в ряды по степеням
,
сходящиеся в некотором интервале
и свободный член
разлагаются в ряды по степеням
,
сходящиеся в некотором интервале
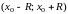 ,
искомое решение
,
искомое решение
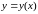 находится в виде степенного ряда
находится в виде степенного ряда
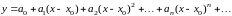
с неопределенными коэффициентами.
При помощи начальных условий находим
коэффициенты
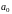 и
и
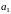 .
Для нахождения последующих коэффициентов
степенной ряд дифференцируем два раза
(каков порядок уравнения) и подставляем
выражения для функции
и ее производных в исходное уравнение,
заменив в нем
,
их разложениями. В результате получаем
тождество, из которого методом
неопределенных коэффициентов находим
недостающие коэффициенты.
.
Для нахождения последующих коэффициентов
степенной ряд дифференцируем два раза
(каков порядок уравнения) и подставляем
выражения для функции
и ее производных в исходное уравнение,
заменив в нем
,
их разложениями. В результате получаем
тождество, из которого методом
неопределенных коэффициентов находим
недостающие коэффициенты.
Построенный степенной ряд сходится в том же интервале и является решением исходного уравнения.
Пример 7.13. Найти решение уравнения
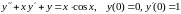 .
.
используя метод неопределенных коэффициентов.
Решение. Разложим коэффициенты уравнения и при в степенные ряды
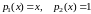 ,
,
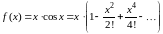 .
.
Решение исходного дифференциального уравнения находим в виде степенного ряда
 .
.
Тогда
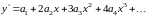 ,
,
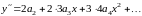 .
.
Из начальных условий находим:
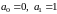 .
Подставляем полученные ряды в
дифференциальное уравнение:
.
Подставляем полученные ряды в
дифференциальное уравнение:
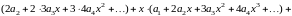
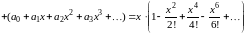 .
.
Приравнивая коэффициенты при одинаковых степенях :
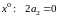 ,
,
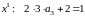 ,
,
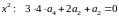 ,
,
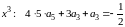 ,
,
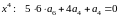 ,
,
……………………………
Отсюда находим, что
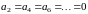 ,
,
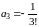 ,
,
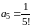 ,
,
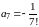 ,
… . Таким образом, получаем решение
уравнения в виде
,
… . Таким образом, получаем решение
уравнения в виде
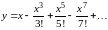 ,
,
т.е.
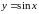 .
.
