32. Функциональный ряд. Точка сходимости. Область сходимости функциональног

7.1. Функциональные ряды

Определение 7.1. Пусть функции 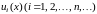определены в области 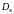. Тогда выражение вида

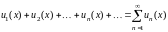(7.1)

называется функциональным рядом.

Придавая определенные значения 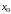, получаем числовой ряд

,

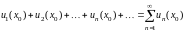который может быть как сходящимся, так и расходящимся.

Определение 7.2. Если числовой ряд 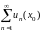сходится при 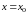, то ряд называется сходящимся в точке , а сама точка называется точкой сходимости ряда. Множество значений , при которых ряд (7.1) сходится, называется областью сходимости функционального ряда.

Область сходимости функционального ряда обозначим 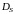. Как правило, область не совпадает с областью , а является ее подмножеством, т.е. .

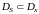Пример 7.1. Найти область сходимости функционального ряда

.

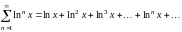Решение. Область определения функций – это .

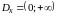Данный ряд является членом геометрической прогрессии со знаменателем 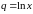. Такой ряд сходится, если .

  .

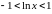
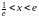Поэтому область сходимости исследуемого ряда является интервал 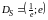. Таким образом, .

Так как каждому 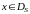соответствует некоторое число – сумма числового ряда, то указанное соответствие определяет функцию , которая называется суммой ряда (7.1) в области . Сумма функционального ряда в области сходимости определяется равенством

,

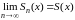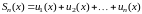
где  -я частичная сумма функционального ряда.

В таком случае 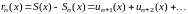 есть -й остаток функционального ряда. В области сходимости ряда .

Пример 7.2. Найти область сходимости и сумму функционального ряда

.

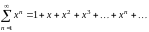Решение. Данный ряд является рядом геометрической прогрессии со знаменателем 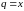. Следовательно, этот ряд сходится при 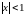, т.е. при всех . Таким образом, область сходимости .

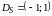В области сходимости данного функционального ряда найдем сумму. По формуле суммы геометрической прогрессии при получаем

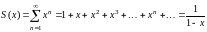, при .

33. Степенной ряд. Сформулировать и доказать теорему Абеля.

Определение 7.3. Степенным рядом называется функциональный ряд вида

, (7.2)

где 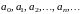 постоянные числа, называемые коэффициентами ряда,  фиксированное число.

При получаем степенной ряд вида

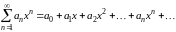. (7.3)

Ряд (7.2) легко приводится к ряду (7.3), если положить 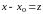. Поэтому при изучении степенных рядов иногда ограничиваются степенным рядом (7.3).

Выясним вопрос о сходимости степенного ряда (7.3). Область сходимости этого степенного ряда содержит, по крайней мере, одну точку 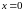(ряд (7.2) сходится в точке ).

Об области сходимости степенного ряда можно судить, исходя из следующей теоремы.

Теорема 7.1 (теорема Абеля). Если степенной ряд (7.3) сходится в точке 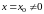, то он абсолютно сходится при всех , удовлетворяющих неравенству

.

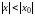Доказательство. Рассмотрим числовой ряд 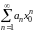, который сходится по условию. Следовательно, по необходимому признаку сходимости 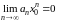. Поэтому все члены ряда ограничены в своей совокупности, т.е. существует такое постоянное положительное число , что при всех имеет место неравенство .

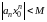Запишем ряд (7.3) следующим образом:

,

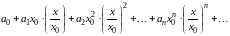и составим ряд из абсолютных членов

.

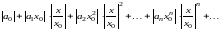В силу установленного неравенство каждый член здесь меньше соответствующего члена геометрической прогрессии со знаменателем : .

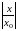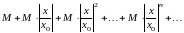Если , то 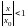и прогрессия сходится. Поэтому сходится и ряд, составленный из абсолютных величин. А значит, абсолютно сходится ряд (7.3).

Несмотря на то, чт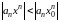о , мы не можем сразу воспользоваться признаком сравнения,поскольку в условии теоремы не сказано, что ряд в самой точке сходится абсолютно.

Следствие. Если степенной ряд (7.3) расходится в точке , то он расходится и при всех , удовлетворяющих неравенству

.
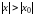