31. Знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимости рядов.

6.1. Знакочередующиеся ряды. Признак Лейбница

Рассмотрим важный класс рядов, у членов которых поочередно изменяются знаки. Такие ряды называются знакочередующиеся.

Определение 6.1. Знакочередующимся рядом называется ряд вида

, (6.1)

где 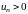для всех 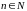(т.е. ряд, положительные и отрицательные члены которого следуют друг за другом поочередно).

Для знакочередующихся рядов имеет место достаточный признак сходимости, установленный в 1714 г. Лейбницем в письме к И.Бернулли.

Теорема 6.1 (признак Лейбница). Знакочередующийся ряд (6.1) сходится, если

1. последовательность абсолютных величин ряда монотонно убывает, т.е.

;

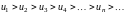2. общий член ряда стремится к нулю, т.е.

.

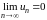При этом сумма ряда (6.1) удовлетворяет неравенствам .

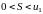Следствие. Остаток ряда (6.1) по абсолютной величине меньше абсолютной величины первого из отбрасываемых членов, т.е.

.

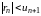Например, по признаку Лейбница ряд

сходится, т.к. выполняются условия теоремы 6.1:

1) 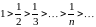; 2) .

2. Абсолютная и условная сходимости рядов

Знакочередующийся ряд является частным случаем знакопеременного ряда.

Определение 6.2. Числовой ряд 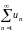, члены которого после любого номера 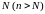имеют разные знаки, называется знакопеременным.

Для знакопеременных рядов имеет место следующий общий достаточный признак сходимости.

Теорема 6.2. Пусть дан знакопеременный ряд

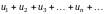. (6.2)

Если сходится ряд, составленный из модулей членов данного ряда

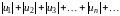, (6.3)

то сходится и сам знакопеременный ряд (6.2).

Надо отметить, что обратное утверждение неверно: если сходится ряд (6.2), то это не означает, что будет сходиться ряд (6.3).

Определение 6.3. Знакопеременный ряд называется абсолютно сходящимся, если ряд, составленный из модулей его членов, сходится.

Знакопеременный ряд называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.

Среди знакопеременных рядов абсолютно сходящиеся ряды занимают особое место. Такие ряды обладают рядом свойств, которые сформулируем без доказательства.

1. Если ряд абсолютно сходится и имеет сумму , то ряд, полученный из него перестановкой членов, также сходится и имеет ту же сумму , что и исходный ряд (теорема Дирихле).

2. Абсолютно сходящиеся ряды с суммами и можно почленно складывать (вычитать). В результате получается абсолютно сходящийся ряд, сумма которого равна (или соответственно ).

3. Под произведением двух рядов 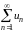и 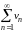понимается ряд вида:

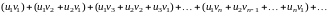
Произведение двух абсолютно сходящихся рядов с суммами и есть абсолютно сходящийся ряд, сумма которого равна .

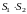Таким образом, абсолютно сходящиеся ряды суммируются, вычитаются, перемножаются как обычные ряды. Суммы таких рядов не зависит от порядка записи членов.

В случае условно сходящихся рядов соответствующие утверждения (свойства), вообще говоря, не имеют места.

Так, переставляя члены условно сходящегося ряда, можно добиться того, что сумма ряда измениться. Например, ряд условно сходится по признаку Лейбница. Пусть сумма этого ряда равна . Перепишем его члены так, что после одного положительного члена будут идти два отрицательных. Получим ряд

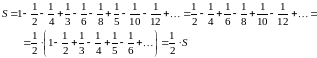
Сумма уменьшилась вдвое!

Более того, путем перестановки членов условно сходящегося ряда можно получить сходящийся ряд с заранее заданной суммой или расходящийся ряд (теорема Римана).

Поэтому действия над рядами нельзя производить, не убедившись в их абсолютной сходимости. Для установления абсолютной сходимости используют все признаки сходимости числовых рядов с положительными членами, заменяя всюду общий член его модулем.

Пример 6.1. Исследовать на сходимость ряд .

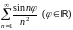Решение. Исходный ряд знакопеременный. Рассмотрим ряд, составленный из абсолютных величин членов данного ряда, т.е. ряд 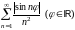. Так как 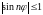, то члены сходного ряда не больше членов ряда Дирихле 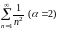, который, как известно, сходится. Следовательно, на основании признака сравнения данный ряд сходится абсолютно. 

Пример 6.2. Исследовать на сходимость ряд .

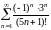Решение. 1) Данный ряд знакочередующийся. Используем признак Лейбница. Проверим, выполняются ли условия.

1.  выполняется;

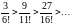2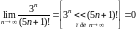.  выполняется.

Следовательно, исходный ряд сходится.

2) Рассмотрим ряд, составленный из абсолютных членов 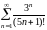. Исследуем его на сходимость, используя признак Даламбера

.

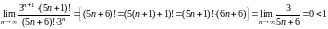По признаку Даламбера ряд, составленный из абсолютных членов, сходится. Значит, исходный знакочередующийся ряд сходится абсолютно. 

Пример 6.3. Исследовать на сходимость ряд .

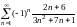Решение. 1) Данный ряд знакочередующийся. Используем признак Лейбница. Проверим, выполняются ли условия.

1.  выполняется;

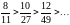2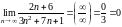.  выполняется.

Следовательно, исходный ряд сходится.

2) Рассмотрим ряд, составленный из абсолютных членов 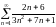. Исследуем его на сходимость, используя предельный признак сравнения. Рассмотрим гармонический ряд 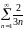, который расходится.

.

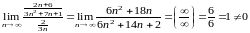Следовательно, оба ряда ведут себя одинаково, т.е. ряд, составленный из абсолютных членов, тоже расходится. Значит, исходный знакочередующийся ряд сходится условно. 

Пример 6.4. Исследовать на сходимость ряд .

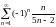Решение. Данный ряд знакочередующийся. Используем признак Лейбница. Проверим, выполняются ли условия.

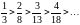1.  выполняется;

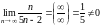2.  не выполняется.

Следовательно, исходный ряд расходится.



Пример 6.5. Вычислить сумму ряда 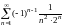с точностью .

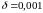Решение. Данный ряд знакочередующийся. По признаку Лейбница этот ряд является сходящимся. Значит, величина отброшенного при вычислении остатка ряда, который также является знакочередующимся рядом, не превосходит первого отброшенного члена (на основании следствия из признака Лейбница).

Нужное число членов найдем путем подбора из неравенства 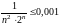. При последнее неравенство выполняется, значит, если отбросить в данном ряде все члены, начиная с шестого, то требуемая точность будет обеспечена. Следовательно,

.