Потенциальное векторное поле

Определение 4.13. Векторное поле называется потенциальным или безвихревым, или градиентным в односвязной области , если в каждой точке этой области

.

Примером потенциального поля является электрическое поле напряженности точечного заряда и другие.

Приведем некоторые свойства потенциального поля:

1. Циркуляция потенциального поля по любому замкнутому контуру в этом поле равна нулю.

В частности, для силового потенциального поля это означает, что работа силы по любому замкнутому контуру равна нулю. В поле скоростей текущей жидкости равенство означает, что в потоке нет замкнутых струек, т.е. нет водоворотов.

2. В потенциальном поле криволинейный интеграл 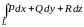вдоль любой кривой с началом в точке и концом в точке 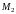зависит только от положения точек и , и не зависит от формы кривой.

3. Потенциальное поле является полем градиента некоторой скалярной функции 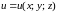, т.е. если , то существует функция такая, что .

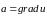Из равенства 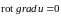следует обратное утверждение: поле градиента скалярной функции является потенциальным.

Для того чтобы поле было потенциальным в области , необходимо и достаточно, чтобы существовала дважды непрерывно дифференцируемая скалярная функция , такая, что 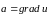, которая называется потенциальной функцией (потенциалом) поля .

Потенциал векторного поля можно найти по следующей формуле:

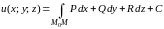, (4.16)

где 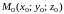 некоторая фиксированная точка области ,  любая точка области ,  произвольная постоянная.

Гармоническое векторное поле

Определение 4.14. Векторное поле называется гармоническим или лапласовым, если оно одновременно является потенциальным и соленоидальным, т.е. если

и .

Примером гармонического поля является поле линейных скоростей стационарного безвихревого потока жидкости при отсутствии в нем источников и стоков.

Потенциал гармонического поля является решением уравнения Лапласа

.

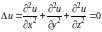Функция , удовлетворяющая уравнению Лапласа, называется гармонической.

Пример 4.9. Выяснить, является ли векторное поле

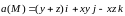
соленоидальным, потенциальным или гармоническим.

Решение. Находим :

.

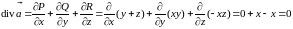Находим :

.

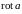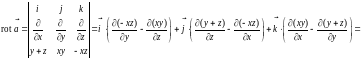
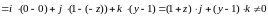Так как , а 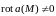, то данное векторное поле является соленоидальным.



27.Числовой ряд. -ая частичная сумма ряда. Сходимость и расходимость ряда. Некоторые свойства рядов. -ый остаток ряда.

5.1. Основные понятия

Бесконечные ряды широко используются в теоретических исследованиях математического анализа, имеют разнообразные практические применения.

Определение 5.1. Числовым рядом (или просто рядом) называется выражение вида

, (5.1)

где 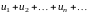 члены ряда (действительные или комплексные числа), число 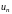 общий член ряда.

Ряд считается заданным, если известно правило, по которому для любого номера можно записать соответствующий член ряда: .

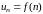Если формула дана, то можно сразу написать любой член ряда. Например, если 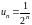, то ряд имеет вид: 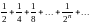. Если 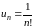( 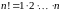), то ряд имеет вид: .

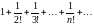Иногда ряд задается при помощи рекуррентного соотношения, связывающего последующий член ряда с предыдущим. При этом задается несколько первых членов ряда и формула, по которой находятся следующие члены ряда. Например, пусть 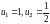, а рекуррентная формула такова: 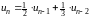. Последовательно находим 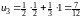; 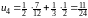и т.д. Таким образом, получаем ряд

.

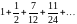Определение 5.2. Сумма конечного числа первых членов ряда называется -й частичной суммой ряда:

.

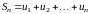Рассмотрим частичные суммы

,

,

………………….

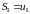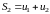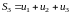
Если существует конечный предел 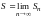, то этот предел называют суммой ряда (5.1) и говорят, что ряд сходится. Если 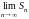не существует или , то ряд (5.1) расходится и суммы не имеет. Например, ряд сходится и его сумма равна 0; ряд 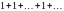расходится, так как при ; ряд 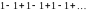расходится, так как последовательность частичных сумм не имеет предела.

Пример 5.1. Дан ряд 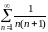. Установить сходимость этого ряда и найти его сумму.

Решение. Запишем -ю частичную сумму данного ряда и преобразуем ее:

.

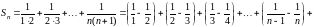
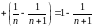Поскольку

,

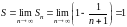то данный ряд сходится и его сумма .



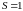Пример 5.2. Исследовать сходимость ряда

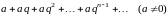, (5.2)

который называется геометрической прогрессией.

Решение. Сумма первых членов прогрессии находится по формуле

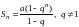
или

.

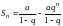1) Если 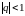, то 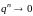при , следовательно

.

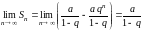Значит, в случае ряд (5.2) сходится и его сумма .

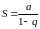2) Если , то 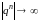при . Поэтому 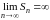. А значит, в случае ряд (5.2) расходится.

3) Если 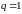, то ряд (5.2) имеет следующий вид: 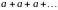. В этом случае 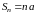, следовательно , т.е ряд расходится.

4) Если 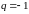, то ряд (5.2) имеет вид: 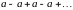. В этом случае

.

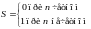Следовательно, 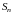предела не имеет – ряд расходится.

Итак, ряд геометрической прогрессии сходится при и расходится при .



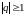Рассмотрим некоторые важные свойства рядов (без доказательства).

1. Если ряд (5.1) сходится и его сумма равна , то ряд

, (5.3)

где  произвольное число, также сходится и его сумма равна 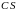. Если же ряд (5.1) расходится и 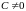, то и ряд (5.3) расходится.

2. Если ряды

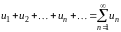
и

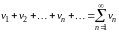
сходятся и их суммы соответственно равны и , то ряды

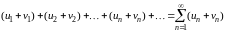(5.4)

и

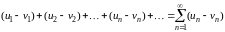(5.5)

также сходятся и их суммы соответственно равны 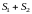и .

3. Если к ряду (5.1) прибавить (или отбросить) конечное число членов, то полученный ряд и ряд (5.1) сходится или расходится одновременно.

Рассмотрим сходящийся ряд (5.1)

.

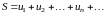Разность между суммой ряда и его -й частичной суммой называется -м остатком ряда. Остаток ряда есть в свою очередь сумма бесконечного ряда. Обозначим остаток ряда 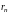. Тогда имеем

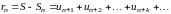. (5.6)

Если ряд (5.1) сходится, то .
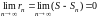