
- •1.1. Двойной интеграл
- •2. Геометрический и физический смысл двойного интеграла. Основные свойства двойного интеграла.
- •4 Вычисление двойного интеграла в полярных координатах
- •5 Приложения двойного интеграла Объем тела
- •Площадь плоской фигуры
- •6 Тройной интеграл
- •1) Разбиваем область на «элементарных областей» .
- •3) Возьмем произвольную точку .
- •5) Составляем интегральную сумму
- •Основные свойства тройного интеграла
- •7 Замена переменной в тройном интеграле. Вычисление тройного интеграла в цилиндрических и сферических координатах.
- •8. Некоторые приложения тройного интеграла в геометрии и физике
- •9. Криволинейный интеграл I рода. Основные свойства кри-I.
- •Основные свойства кри-I
- •10. Вычисление криволинейного интеграла I рода: явное представление кривой, параметрическое представление кривой, полярное представление кривой.
- •2.2. Вычисления криволинейного интеграла I рода
- •11. Некоторые приложения кри-I рода в геометрии и физике.
- •Площадь цилиндрической поверхности
- •12. Криволинейный интеграл II рода. Основные свойства кри-II.
- •Криволинейный интеграл II рода (кри-II)
- •Основные свойства кри-II
- •13. Вычисление кри-II: явное представление кривой, параметрическое представление кривой. Некоторые приложения кри-II.
- •2.5. Вычисления криволинейного интеграла II рода
- •Явное представление кривой
- •Параметрическое представление кривой
- •2.6. Некоторые приложения криволинейного интеграла II рода Площадь плоской фигуры
- •Работа переменной силы
- •14. Формула Остроградского – Грина.
- •15.Поверхностный интеграл I рода. Основные свойства поверхностного интеграла I рода. Вычисление поверхностного интеграла I рода.
- •3.2. Вычисление поверхностного интеграла I рода
- •16.Поверхностный интеграл II рода. Свойства поверхностного интеграла II рода.
- •3.3. Поверхностный интеграл II рода
- •17.Вычисление поверхностного интеграла II рода. Формула Остроградского - Гаусса для вычисления поверхностного интеграла II рода.
- •3.4. Вычисление поверхностного интеграла II рода
- •I способ
- •II способ
- •II способ
- •III способ
- •18. Скалярное поле. Поверхность и линии уровня. Производная по направлению. Градиент.
- •Производная по направлению
- •Градиент
- •19.Векторное поле. Векторные (силовые) линии. Векторная трубка.
- •20. Поток векторного поля через поверхность. Формула вычисления потока векторного поля. Источник и сток. Формула Остроградского – Гаусса для вычисления потока.
- •4.3. Поток векторного поля через поверхность
- •21.Дивергенция поля. Некоторые свойства дивергенции. Физический смысл дивергенции.
- •22. Циркуляция поля. Физический смысл циркуляции поля.
- •4.5. Циркуляция поля
- •23. Ротор поля. Некоторые свойства ротора. Формула Стокса.
- •4.6. Ротор поля. Формула Стокса
- •24. Векторные дифференциальные операции первого порядка.
- •Векторные дифференциальные операции первого и второго порядка
- •25. Векторные дифференциальные операции второго порядка.
- •26.Классификация векторных полей: определения соленоидального, потенциального и гармонического векторного поля.
- •4.8. Классификация векторных полей Соленоидальное векторное поле
- •Потенциальное векторное поле
- •Гармоническое векторное поле
- •27.Числовой ряд. -ая частичная сумма ряда. Сходимость и расходимость ряда. Некоторые свойства рядов. -ый остаток ряда.
- •5.1. Основные понятия
- •28. Сформулировать и доказать необходимый признак сходимости ряда. Достаточный признак расходимости ряда. Гармонический ряд.
- •5.2. Необходимый признак сходимости ряда
- •5.3. Достаточные признаки сходимости ряда
- •29. Признаки сравнения рядов. Признак Даламбера Признаки сравнения рядов.
- •Признак Даламбера
- •30. Радикальный признак Коши. Интегральный признак Коши. Ряд Дирихле.
- •Интегральный признак Коши
- •31. Знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимости рядов.
- •6.1. Знакочередующиеся ряды. Признак Лейбница
- •Абсолютная и условная сходимости рядов
- •32. Функциональный ряд. Точка сходимости. Область сходимости функциональног
- •7.1. Функциональные ряды
- •33. Степенной ряд. Сформулировать и доказать теорему Абеля.
- •34. Интервал и радиус сходимости степенного ряда. Интервал и радиус сходимости
- •Свойства степенных рядов
- •35. Ряды Тейлора и Маклорена. Разложение функций в степенной ряд.
- •Разложение функций в степенной ряд
- •36. Некоторые приложения степенных рядов.
- •Некоторые приложения степенных рядов
- •Вычисление значений функции
- •2. Вычисление интегралов
- •3. Приближенное решение дифференциальных уравнений
- •Способ последовательного дифференцирования
- •Способ неопределенных коэффициентов
- •37. Тригонометрический ряд. Формулы коэффициентов ряда Фурье
- •8.1. Периодические функции. Периодические процессы
- •Тригонометрический ряд Фурье
- •38.Разложение в ряд Фурье -периодических функций. Теорема Дирихле. Разложение в ряд Фурье четных и нечетных функций.
- •8.3. Разложение в ряд Фурье -периодических функций
- •8.4. Разложение в ряд Фурье четных и нечетных функций
- •39. Разложение в ряд Фурье функций произвольного периода.
- •40Уравнение колебаний струны.
- •Уравнение колебаний струны
- •Уравнение теплопроводности.
23. Ротор поля. Некоторые свойства ротора. Формула Стокса.
4.6. Ротор поля. Формула Стокса
Определение 4.11. Ротором (или вихрем) векторного поля
называется
вектор, который обозначается
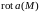 и определяется формулой
и определяется формулой
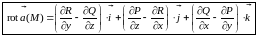 .
(4.13)
.
(4.13)
Формулу (4.13) можно записать с помощью символического определителя, который удобный для запоминания:
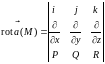 .
.
Отметим некоторые свойства ротора:
Если постоянный вектор, то
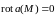 .
.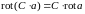 ,
где
.
,
где
.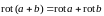 ,
т.е. ротор суммы двух векторных функций
равна сумме дивергенции слагаемых.
,
т.е. ротор суммы двух векторных функций
равна сумме дивергенции слагаемых.Если скалярная функция, а вектор, то
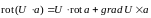 .
.
Используя понятие ротора и циркуляции векторного поля, запишем известную в математическом анализе формулу Стокса:
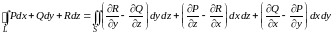 .
.
(4.14)
Эту же формулу Стокса можно записать и векторной форме:
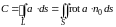 .
(4.15)
.
(4.15)
Формула (4.15) означает следующее: циркуляция векторного поля вдоль замкнутого контура равна потоку ротора этого поля через любую гладкую поверхность , краем которой является контур . Направление обхода по контуру и сторона поверхности одновременно или положительные, или отрицательные.
Как видно из определения, ротор вектора есть векторная величина, образующая собственное векторное поле.
Число
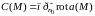
называется
плотностью циркуляции векторного
поля
в точке
в направлении вектора
.
Плотность циркуляции достигает максимума
в направлении
и равна
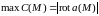 .
.
Так что связь между ротором и циркуляцией аналогична связи между градиентом и производной по направлению.
Пример 4.8. Найти
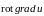 скалярного поля
скалярного поля
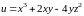 .
.
Решение. Находим градиент скалярного поля . Частные производные первого порядка соответственно равны:
 ;
;
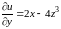 ;
;
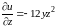 .
.
Находим ротор градиента скалярного поля, используя символическую запись формулы (4.13):
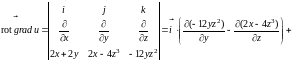
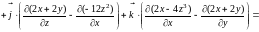
 .
.
24. Векторные дифференциальные операции первого порядка.
Векторные дифференциальные операции первого и второго порядка
Основными дифференциальными операциями (действиями) над скалярным полем и векторным полем являются: градиент, дивергенция, ротор. Эти действия называются векторными операциями первого порядка (в них участвуют только производные первого порядка).
Векторные операции – нахождение
градиента, дивергенции, ротора, удобно
описывать с помощью дифференциального
оператора, который обозначается символом
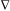 (читается «набла») и называется оператором
Гамильтона:
(читается «набла») и называется оператором
Гамильтона:
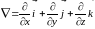 .
.
Он приобретает смысл лишь в комбинации
со скалярными или векторными функциями.
Символическое «умножение» вектора
на скаляр
или вектор
производится по обычным правилам
векторной алгебры, а «умножение» символов
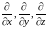 на величины
,
на величины
,
 ,
,
 ,
понимают как взятие соответствующей
частной производной от этих величин.
,
понимают как взятие соответствующей
частной производной от этих величин.
Выразим основные дифференциальные операции с помощью оператора Гамильтона:
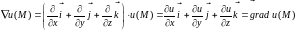 .
.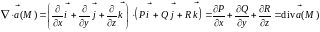 .
. .
.
Оператор Гамильтона применяется для записи и других операций и для вывода различных формул в теории поля. При действии с ними надо пользоваться правилами векторной алгебры и правилами дифференцирования.
После применения оператора Гамильтона
к скалярному или векторному полю
получается новое поле, к которому можно
снова применит этот оператор. В результате
получаются дифференциальные операции
второго порядка. Можно убедиться,
что имеется лишь пять дифференциальных
операций второго порядка:
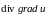 ,
,
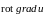 ,
,
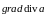 ,
,
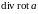 ,
,
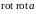 .
Понятно, что, например, операция
.
Понятно, что, например, операция
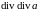 не имеет смысла, так как
не имеет смысла, так как
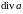 есть скаляр.
есть скаляр.
Дифференциальный оператор
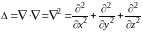
также называется оператором Гамильтона.
Запишем основные дифференциальные операции второго порядка, используя оператор Гамильтона:
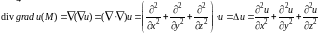 .
.
Таким образом, получаем дифференциальное уравнение
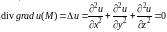 ,
,
которое называется дифференциальным уравнением Лапласа. Это уравнение играет важную роль в различных разделах математической физике. Решениями уравнения Лапласа являются так называемые гармонические функции.
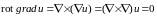 ,
так как векторное произведение двух
одинаковых векторных полей равно
нулевому вектору. Это означает, что
поле градиента есть поле безвихревое.
,
так как векторное произведение двух
одинаковых векторных полей равно
нулевому вектору. Это означает, что
поле градиента есть поле безвихревое.
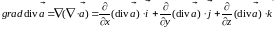 .
.
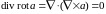 ,
так как смешанное произведение трех
векторов, из которых два одинаковых,
равно нулю.
,
так как смешанное произведение трех
векторов, из которых два одинаковых,
равно нулю.
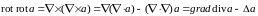 .
.
