20. Поток векторного поля через поверхность. Формула вычисления потока векторного поля. Источник и сток. Формула Остроградского – Гаусса для вычисления потока.

4.3. Поток векторного поля через поверхность

Пусть векторное поле образовано вектором

.

Возьмем в этом поле некоторую поверхность и выберем на ней определенную сторону. Пусть  единичный вектор нормали к рассматриваемой стороне поверхности .

Рассмотрим интеграл по поверхности от скалярного произведения вектора поля на единичный вектор нормали

. ()

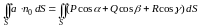Если  поле скоростей текущей жидкости, то интеграл () выражает поток жидкости через поверхность . Независимо от физического смысла поля данный интеграл называют потоком векторного поля через поверхность и обозначают буквой П.

Определение 4.8. Потоком вектора через поверхность называется интеграл по поверхности от скалярного произведения вектора поля на единичный вектор нормали к поверхности, т.е.

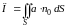. (4.5)

Таким образом, вычисление потока вектора сводится к вычислению интеграла по поверхности. Из самого определения следует, что поток вектора П  величина скалярная. Если изменить направление нормали на противоположный, т.е. переменить сторону поверхности , то поток П изменит знак.

Так как 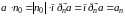, то

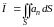, (4.6.)

где 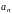 проекция вектора 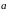на направление нормали , 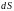 дифференциал (элемент) площадки поверхности.

Поскольку 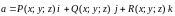, , 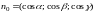то поток (4.5) вектора можно записать в виде

,

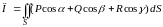или в виде

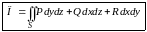. (4.7)

Особый интерес представляет случай, когда поверхность замкнута и ограничивает некоторый объем . Тогда поток вектора записывается в виде 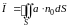. В этом случае за направление вектора обычно берут направление внешней нормали и говорят о потоке изнутри поверхности .

Если векторное поле есть поле скоростей жидкости, то величина потока П через замкнутую поверхность дает разность между количеством жидкости, вытекающей из области (объема ) и втекающей в нее за единицу времени (в точках поверхности , где векторные линии выходят из объема , внешняя нормаль образует с вектором острый угол и 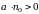, в точках, где векторные линии входят в объем, ).

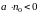При этом, если 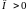, то из области вытекает больше жидкости, чем в нее втекает. Это означает, что внутри области имеются дополнительные источники. Если , то внутри области имеются стоки, поглощающие избыток жидкости.

Можно сказать, что источники – точки, откуда векторные линии начинаются, а стоки – точки, где векторные линии кончаются. Так, в электростатическом поле источником является положительный заряд, стоком – отрицательный заряд магнита (см. рисунок).

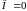Если , то из области вытекает столько же жидкости, сколько в нее втекает в единицу времени; внутри области либо нет ни источников, ни стоков, либо они таковы, что их действие взаимно компенсируется.

Пример 4.4. Вычислить поток векторного поля

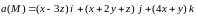
через верхнюю часть плоскости 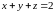, лежащую в первом октанте.

Если  замкнутая кусочно-гладкая поверхность, единичный вектор нормали к которой , то поток П вектора через поверхность можно вычислить с помощью формулы Остроградского – Гаусса:

. (4.8)

Пример 4.5. Найти поток вектора

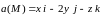
через замкнутую поверхность , ограниченную поверхностям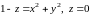и , в направлении внешней нормали.