III способ

Воспользуемся формулой (3.10) и найдем интеграл 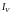по замкнутой поверхности, состоящей в данном примере из четырех поверхностей:

,

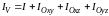где  искомый интеграл

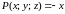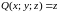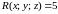Итак, , и . Тогда

,

где 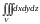 объем пирамиды, ограниченной четырьмя поверхностями.

Далее получаем

.

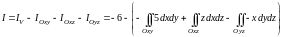Знаки для поверхностных интегралов выбирается согласно тому, какой угол образуют нормальные векторы к каждой рассматриваемой плоскости и соответствующей координатной осью.

Тогда

.

,

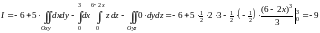18. Скалярное поле. Поверхность и линии уровня. Производная по направлению. Градиент.

Полем называется область пространства, в каждой точке которой определено значение некоторой величины.

Если каждой точке этой области определено число 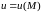, говорят, что в области определено (задано) скалярное поле или функция точки. Иначе можно сказать, что скалярное поле – это скалярная функция 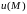вместе с ее областью определения.

Если каждой точке области пространства соответствует некоторый вектор 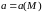, то говорят, что задано векторное поле или векторная функция точки.

Если функция или 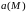не зависят от времени, то скалярное или векторное поле называется стационарным (или установившимся). Поле, которое меняется с течением времени (например, меняется скалярное поле температуры при охлаждении тела), называется нестационарным (или неустановившимся).

.4.1. Скалярное поле

Определение 4.1. Если в области 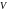задана скалярная функция точки , то говорят, что в этой области задано скалярное поле.

Если  область трехмерного пространства, то скалярное поле можно рассматривать как функцию трех переменных 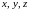 координат точки , т.е.

.

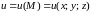Если скалярная функция зависит только от двух переменных и , то соответствующее скалярное поле 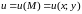называют плоским.

В дальнейшем будем предполагать, что скалярная функция 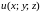 определяющая скалярное поле, непрерывна вместе со своими частными производными.

Для наглядного представления скалярного поля используют поверхности и линии уровня.

Определение 4.2. Поверхностью уровня скалярного поля называется геометрическое место точек, в которых функция принимает постоянное значение, т.е.

.

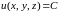В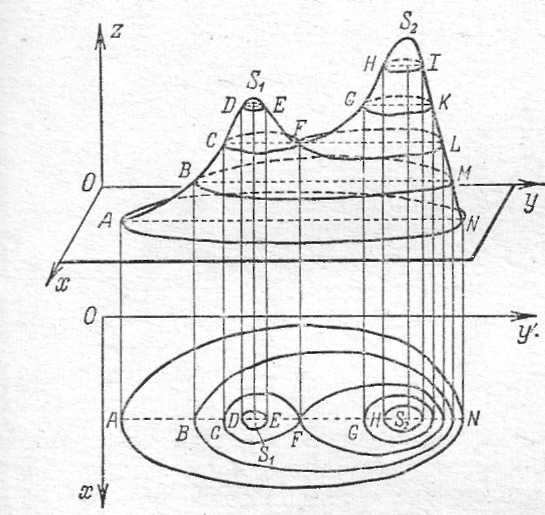 случае плоского поля 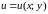равенство 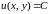представляет собой уравнение линии уровня поля – линии на плоскости , в точках которой функция сохраняет постоянное значение.

Пусть скалярное поле задано

функцией 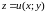, где значения

откладываются по оси . Линиями

уровня на плоскости будут проек-

ции линий, которые получаются в пере-

сечении поверхности с плос-

костями 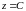(см. рисунок).

Линии уровня применяются в

математике при исследовании поверх-

ностей методом сечений.

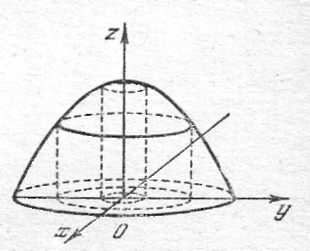
Пример 4.1. Определить линии

уровня функции .

Решение.

Линиями уровня будут линии с уравнениями 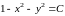. Это окружности на плоскости с радиусом 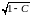(см. рисунок).

В частности, при 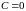получаем окружность .



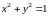Основными понятиями скалярного поля являются «производная по направлению» и «градиент».

Производная по направлению

Пусть задано скалярное поле, т.е. задана функция 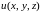, и точка 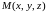. Будем предполагать, что функция непрерывна и имеет непрерывные производные по своим аргументам в области .

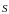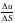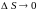Определение 4.3. Производной от функции в точке по направлению вектора называется предел отношения при , т.е.

.

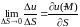Если функция дифференцируемая, то производная от функции в точке по направлению вектора находится по следующей формуле:

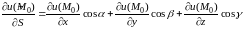, (4.1)

где 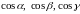 направляющие косинусы вектора .

В случае функции двух переменных , т.е. когда поле плоское, формула (4.1) примет следующий вид:

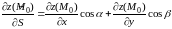, (4.2)

где .

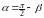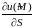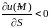Подобно тому, как частные производные характеризуют скорость изменения функции в направлении осей координат, так и производная по направлению будет являться скоростью изменения функции в точке по направлению вектора . Если , то функция возрастает в направлении , если , то функция убывает в направлении .