
- •1.1. Двойной интеграл
- •2. Геометрический и физический смысл двойного интеграла. Основные свойства двойного интеграла.
- •4 Вычисление двойного интеграла в полярных координатах
- •5 Приложения двойного интеграла Объем тела
- •Площадь плоской фигуры
- •6 Тройной интеграл
- •1) Разбиваем область на «элементарных областей» .
- •3) Возьмем произвольную точку .
- •5) Составляем интегральную сумму
- •Основные свойства тройного интеграла
- •7 Замена переменной в тройном интеграле. Вычисление тройного интеграла в цилиндрических и сферических координатах.
- •8. Некоторые приложения тройного интеграла в геометрии и физике
- •9. Криволинейный интеграл I рода. Основные свойства кри-I.
- •Основные свойства кри-I
- •10. Вычисление криволинейного интеграла I рода: явное представление кривой, параметрическое представление кривой, полярное представление кривой.
- •2.2. Вычисления криволинейного интеграла I рода
- •11. Некоторые приложения кри-I рода в геометрии и физике.
- •Площадь цилиндрической поверхности
- •12. Криволинейный интеграл II рода. Основные свойства кри-II.
- •Криволинейный интеграл II рода (кри-II)
- •Основные свойства кри-II
- •13. Вычисление кри-II: явное представление кривой, параметрическое представление кривой. Некоторые приложения кри-II.
- •2.5. Вычисления криволинейного интеграла II рода
- •Явное представление кривой
- •Параметрическое представление кривой
- •2.6. Некоторые приложения криволинейного интеграла II рода Площадь плоской фигуры
- •Работа переменной силы
- •14. Формула Остроградского – Грина.
- •15.Поверхностный интеграл I рода. Основные свойства поверхностного интеграла I рода. Вычисление поверхностного интеграла I рода.
- •3.2. Вычисление поверхностного интеграла I рода
- •16.Поверхностный интеграл II рода. Свойства поверхностного интеграла II рода.
- •3.3. Поверхностный интеграл II рода
- •17.Вычисление поверхностного интеграла II рода. Формула Остроградского - Гаусса для вычисления поверхностного интеграла II рода.
- •3.4. Вычисление поверхностного интеграла II рода
- •I способ
- •II способ
- •II способ
- •III способ
- •18. Скалярное поле. Поверхность и линии уровня. Производная по направлению. Градиент.
- •Производная по направлению
- •Градиент
- •19.Векторное поле. Векторные (силовые) линии. Векторная трубка.
- •20. Поток векторного поля через поверхность. Формула вычисления потока векторного поля. Источник и сток. Формула Остроградского – Гаусса для вычисления потока.
- •4.3. Поток векторного поля через поверхность
- •21.Дивергенция поля. Некоторые свойства дивергенции. Физический смысл дивергенции.
- •22. Циркуляция поля. Физический смысл циркуляции поля.
- •4.5. Циркуляция поля
- •23. Ротор поля. Некоторые свойства ротора. Формула Стокса.
- •4.6. Ротор поля. Формула Стокса
- •24. Векторные дифференциальные операции первого порядка.
- •Векторные дифференциальные операции первого и второго порядка
- •25. Векторные дифференциальные операции второго порядка.
- •26.Классификация векторных полей: определения соленоидального, потенциального и гармонического векторного поля.
- •4.8. Классификация векторных полей Соленоидальное векторное поле
- •Потенциальное векторное поле
- •Гармоническое векторное поле
- •27.Числовой ряд. -ая частичная сумма ряда. Сходимость и расходимость ряда. Некоторые свойства рядов. -ый остаток ряда.
- •5.1. Основные понятия
- •28. Сформулировать и доказать необходимый признак сходимости ряда. Достаточный признак расходимости ряда. Гармонический ряд.
- •5.2. Необходимый признак сходимости ряда
- •5.3. Достаточные признаки сходимости ряда
- •29. Признаки сравнения рядов. Признак Даламбера Признаки сравнения рядов.
- •Признак Даламбера
- •30. Радикальный признак Коши. Интегральный признак Коши. Ряд Дирихле.
- •Интегральный признак Коши
- •31. Знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимости рядов.
- •6.1. Знакочередующиеся ряды. Признак Лейбница
- •Абсолютная и условная сходимости рядов
- •32. Функциональный ряд. Точка сходимости. Область сходимости функциональног
- •7.1. Функциональные ряды
- •33. Степенной ряд. Сформулировать и доказать теорему Абеля.
- •34. Интервал и радиус сходимости степенного ряда. Интервал и радиус сходимости
- •Свойства степенных рядов
- •35. Ряды Тейлора и Маклорена. Разложение функций в степенной ряд.
- •Разложение функций в степенной ряд
- •36. Некоторые приложения степенных рядов.
- •Некоторые приложения степенных рядов
- •Вычисление значений функции
- •2. Вычисление интегралов
- •3. Приближенное решение дифференциальных уравнений
- •Способ последовательного дифференцирования
- •Способ неопределенных коэффициентов
- •37. Тригонометрический ряд. Формулы коэффициентов ряда Фурье
- •8.1. Периодические функции. Периодические процессы
- •Тригонометрический ряд Фурье
- •38.Разложение в ряд Фурье -периодических функций. Теорема Дирихле. Разложение в ряд Фурье четных и нечетных функций.
- •8.3. Разложение в ряд Фурье -периодических функций
- •8.4. Разложение в ряд Фурье четных и нечетных функций
- •39. Разложение в ряд Фурье функций произвольного периода.
- •40Уравнение колебаний струны.
- •Уравнение колебаний струны
- •Уравнение теплопроводности.
1.1. Двойной интеграл
Рассмотрим в плоскости
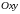 замкнутую область
замкнутую область
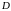 .
Область
называется замкнутой, если она ограничена
замкнутой линией, и точки, лежащие на
границе, считаются принадлежащими
области
.
.
Область
называется замкнутой, если она ограничена
замкнутой линией, и точки, лежащие на
границе, считаются принадлежащими
области
.
Пусть в области
задана непрерывная функция
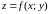 .
.
1) Разбиваем область
на
 «элементарных областей»
«элементарных областей»
 .
.
2) Площадь области
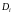 обозначим
обозначим
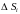 ,
а диаметр (наибольшее расстояние между
двумя точками области) – через
,
а диаметр (наибольшее расстояние между
двумя точками области) – через
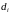 .
.
3) Возьмем произвольную точку
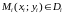 .
.
4) Находим
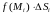 ,
что равно объему тела (призма), площадь
основания которого
,
а высота равна
,
что равно объему тела (призма), площадь
основания которого
,
а высота равна
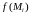 .
.
5) Составляем интегральную сумму
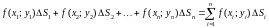 .
.
6) Обозначим через
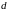 длину наибольшего из диаметров
«элементарных областей», т.е.
длину наибольшего из диаметров
«элементарных областей», т.е.
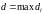 ,
,
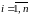 .
Найдем предел интегральной суммы, когда
.
Найдем предел интегральной суммы, когда
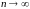 так, что
так, что
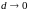 .
Если предел существует и не зависит от
способа разбиения области
на части, ни от выбора точек в них, то он
называется двойным интегралом
от функции
по области
.
.
Если предел существует и не зависит от
способа разбиения области
на части, ни от выбора точек в них, то он
называется двойным интегралом
от функции
по области
.
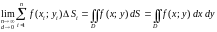 .
.
Таким образом, двойным интегралом
от
по замкнутой областью
называется предел интегральной суммы
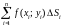 ,
когда число «элементарных областей»
неограниченно возрастает, а длина
наибольшего диаметра стремится к нулю:
,
когда число «элементарных областей»
неограниченно возрастает, а длина
наибольшего диаметра стремится к нулю:
 .
(1.1)
.
(1.1)
интегрируемая функция в
области
;
область
интегрирования; и
и
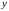 переменные
интегрирования dx
dy или dS
элемент площади.
переменные
интегрирования dx
dy или dS
элемент площади.
2. Геометрический и физический смысл двойного интеграла. Основные свойства двойного интеграла.
Если функция непрерывна в замкнутой области ,то она интегрируема в этой области.
Замечание: далее будем рассматривать только функции, непрерывные в области интегрирования, хотя двойной интеграл может существовать не только для непрерывных функций.
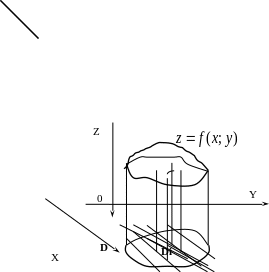
Геометрический смысл двойного интеграла.
Двойной интеграл от неотрицательной
функции (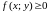 )
численно равен объему тела, которое
сверху ограничено поверхностью
,
снизу – замкнутой областью
плоскости
,
с боков – цилиндрической поверхностью,
образующая которой параллельна оси
)
численно равен объему тела, которое
сверху ограничено поверхностью
,
снизу – замкнутой областью
плоскости
,
с боков – цилиндрической поверхностью,
образующая которой параллельна оси
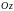 ,
а направляющей служит граница
,
т.е.
,
а направляющей служит граница
,
т.е.
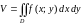 .
.
Физический смысл двойного интеграла.
Двойной интеграл от функции
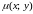 численно равен массе плоской пластины,
если подынтегральная функция
считать плотностью этой пластины в
точке
численно равен массе плоской пластины,
если подынтегральная функция
считать плотностью этой пластины в
точке
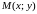 ,
т.е.
,
т.е.
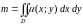 .
.
Основные свойства двойного интеграла
Свойства двойного интеграла аналогичны свойствам определенного интеграла функции одной переменной на отрезке. Поэтому перечислим основные свойства двойного интеграла (без доказательства), считая подынтегральные функции интегрируемыми.
1.
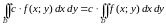 ,
где
,
где
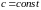 .
.
2.
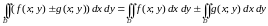 .
.
3. Если область
разбить линией на две области
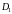 и
и
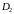 такие, что
такие, что
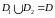 ,
а пересечение
,
а пересечение
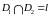 ,
где
,
где
 линия, разделяющая
и
(см. рисунок), то
линия, разделяющая
и
(см. рисунок), то
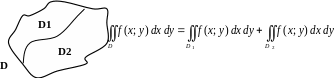
4. Если в области имеет место неравенство , то и
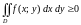 .
.
5. Если в области
функции
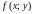 и
и
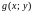 удовлетворяют неравенству
удовлетворяют неравенству
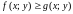 ,
то и
,
то и
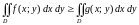 .
.
6. Если
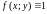 ,
,
 ,
то
,
то
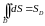 ,
где
,
где
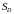 площадь области
интегрирования
.
площадь области
интегрирования
.
7. Если функция
непрерывна в замкнутой области
,
площадь которой
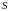 ,
то
,
то
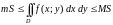 ,
,
где
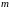 и
и
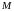 соответственно
наименьшее и наибольшее значения
подынтегральной функции в области
.
соответственно
наименьшее и наибольшее значения
подынтегральной функции в области
.
8. Если функция
непрерывна в замкнутой области
,
площадь которой
,
то в этой области существует такая точка
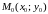 ,
что
,
что
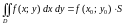 .
.
Величину
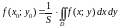 называют средним значением
функции
в области
.
называют средним значением
функции
в области
.
3Вычисление двойного интеграла в декартовых координатах
Покажем, что вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов.
Пусть требуется вычислить двойной
интеграл
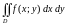 ,
где функция
непрерывна в области
.
Тогда, двойной интеграл выражает объем
цилиндрического тела, ограниченного
сверху поверхностью
.
Найдем этот объем, используя метод
параллельных сечений. Ранее было
показано, что
,
где функция
непрерывна в области
.
Тогда, двойной интеграл выражает объем
цилиндрического тела, ограниченного
сверху поверхностью
.
Найдем этот объем, используя метод
параллельных сечений. Ранее было
показано, что
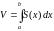 ,
где
,
где
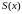 площадь сечения
плоскостью, перпендикулярной оси
площадь сечения
плоскостью, перпендикулярной оси
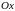 ,
а
,
а
 и
и
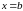 уравнения плоскостей,
ограничивающих данное тело.
уравнения плоскостей,
ограничивающих данное тело.

направлении
оси
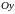 :
любая прямая, параллельная оси
,
пересекает границу области не более
чем в дух точках.
:
любая прямая, параллельная оси
,
пересекает границу области не более
чем в дух точках.
Построим сечение цилиндрического тела
плоскостью, перпендикулярной оси
:
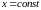 ,
где
,
где
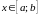 .
.
В сечении получаем криволинейную
трапецию
 ,
ограниченную линиями
,
где
,
,
ограниченную линиями
,
где
,
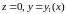 и
и
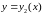 .
Площадь
этой трапеции находим с помощью
определенного интеграла:
.
Площадь
этой трапеции находим с помощью
определенного интеграла:
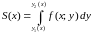 .
.
Теперь, согласно методу параллельных сечений, искомый объем цилиндрического тела может быть найден так:
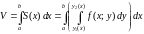 .
.
С другой стороны, объем цилиндрического тела определяется как двойной интеграл от функции по области . Следовательно,
 .
.
Таким образом, для вычисления двойного интеграла функции по области используется следующая формула
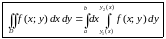 .
(1.2)
.
(1.2)
Правую часть (1.2) называют двукратным
(или повторным) интегралом
от функции
по области
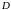 .
Интеграл
.
Интеграл
 называется внутренним интегралом.
называется внутренним интегралом.
Для вычисления двукратного интеграла
сначала берем внутренний интеграл,
считая
постоянным, затем берем внешний интеграл,
т.е. результат первого интегрирования
интегрируем по
в пределах от
 до
до
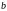 .
.
Если область
ограничена прямыми
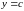 и
и
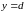 (
(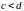 ),
кривыми
),
кривыми
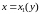 и
и
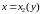 ,
причем
,
причем
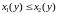 для всех
для всех
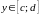 ,
т.е. область
правильная
(стандартная) в направлении оси
,
то, рассекая тело плоскостью
,
т.е. область
правильная
(стандартная) в направлении оси
,
то, рассекая тело плоскостью
 ,
аналогично получаем
,
аналогично получаем
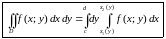 .
(1.3)
.
(1.3)
Здесь при вычислении внутреннего интеграла, считаем постоянным.
Замечания.
1. Формулы (1.2) и (1.3) справедливы и в
случае, когда
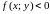 ,
,
 .
.
2. Если область правильная в обоих направлениях, то двойной интеграл можно вычислять как и по формуле (1.2), так и по формуле (1.3).
3. Если область не является правильной ни «по », ни «по », то для сведения двойного интеграла к повторным ее следует разбить на части, правильные в направлении оси или оси .
4. Полезно помнить, что внешние пределы в двукратном интеграле всегда постоянны, а внутренние, как правило, переменные.
Пример 1.1. Вычислить
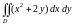 ,
если область
ограничена линиями:
,
если область
ограничена линиями:
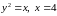 .
.
Решение. I способ.
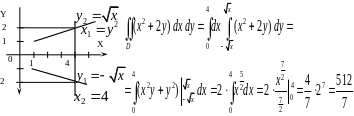
II способ. Построенная область является правильной в направлении оси . Для вычисления двойного интеграла воспользуемся формулой (1.3):
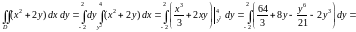
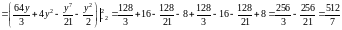 .
.
