Зміна вільної енергії Гібса реакцій при зміні тиску

Для реакций из участю реальних газів при перевищенні тиску над стандартним частка приросту вільної енергії, що залежить від тиску підраховується за рівнянням:

(10)

де V_тв - об’ємний ефект реакції між твердими фазами; p -загальний тиск в системі; 0,1 - стандартний тиск в 0.1 МПа; n - зміна числа молів газу внаслідок реакції, знак залежить від того чи є газ продуктом реакції (плюс), чи вихідною речовиною (мінус); R - газова стала 8,3147 Дж/(К•моль); T - температура Кельвіна; f_i - фугітивність газу (f_i = P_i • _i)

Для реакції із участю тільки конденсованих фаз приймається незмінність об'єму окремих фаз із підвищенням тиску. Тоді

(11)

Зміна вільної енергії Ґібса системи внаслідок зміни температури і тиску визначається в два кроки:

• Спочатку розраховується приріст вільної енергії реакції внаслідок зміни температури при стандартному тиску G_T реакції;

• Сумарний приріст вільної енергії рівняється

(12)

Приклад:

Розрахуємо приріст вільної енергії Ґібса хімічної реакції утворення форстериту при скарнуванні доломіту

2CaMg(CO₃) + SiO₂ = Mg₂[SiO₄] + 2CaCO₃ + 2CO₂

при 300°С та f_CO2=150 МПа.

1.Розрахуємо за рівняннями (3) і (8) G_300°С кожної фази, що беруть участь в реакції  

доломіт	кварц	форстерит	Кальцит	CO2
-2227786	-16527	-2095136	-1163416	-457258

  2. Розрахуємо згідно рівняння реакції сумарне значення G_300°С реагентів та G_300°С продуктів реакції із врахуванням  стехіометричних коефіцієнтів

 G_300°С реагентів = 2·G_300°(доломіт)+  G_300°(кварц)= -4472099

G_300°С продуктів = G_300°(форстерит)+  2·G_300°(кальцит) + 2·G_300°(CO₂)= -5336484

• Розрахуємо G_300°С реакції як різницю

G_300°С реакції = G_300°С продуктів - G_300°С реагентів=

-5336484 – (-4472099) = -864385

Розрахуємо енергетичний ефект реакції в випадку якщо тиск системи створюється вуглекислим газом.

Згідно рівняння (10) спочатку необхідно вирахувати зміну об'єму твердих фаз внаслідок реакції

доломіт	Кварц	форстерит	Кальцит	CO2
64.34	22.688	43.79	36.934

43.79+2*36.934 –(2*64.34+22.688)= -33,71 см³ = -33,71 Дж/МПа

Тоді за рівнянням (10)

``= 2·8,3147·573,15·ln(10·150)Дж + (-33,71Дж/МПа·150МПа) = 64646,83 Дж

Загальна зміна вільної енергії в ході реакції складе

-864385 + 64646,83 = -799738,17

Якщо ми розрахували зміну вільної енергії Ґібса та об'ємний ефект реакції при даній температурі, тоді ми можемо оцінити загальний тиск в системі (знаючи парціальні тиски газів, що беруть участь в реакції) або ж парціальний тиск газу знаючи загальний тиск в системі.

Так, якщо в системі досягнута рівновага, то

член G_T,P рівняння

дорівнює нулю G_T,P = 0. Проігноруємо значення 0,1 МПа стандартного тиску, як зникомо мале в порівнянні із геологічно важливими тисками. Тоді отримаємо рівняння

0 = G_T+V_тв·P±nRT·ln f_i

В випадку твердофазової реакції

P =G_TV_тв

Результати розрахунків занесіть в таблицю вигляду

t,°C	T,K	GT	P,МПа
Vтв=

При участі в реакції газу його фугітивність рівняється

де 2,303 – перехідний коефіцієнт від натурального до десяткового логарифму.

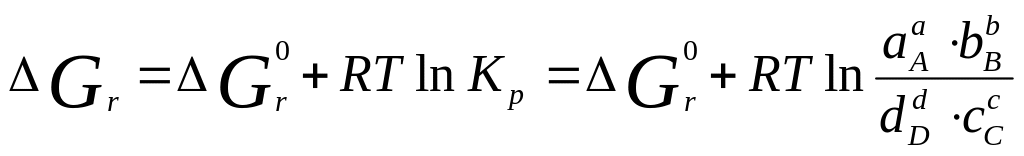
_{В умовах рiвноваги Gr = 0, тодi}

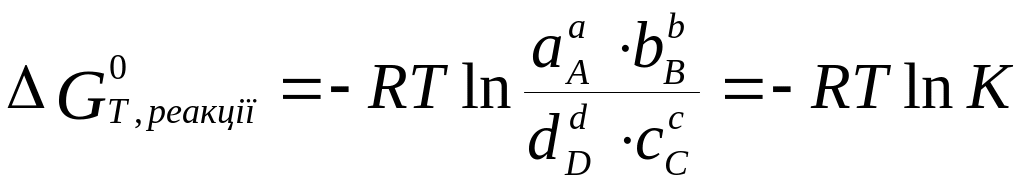
_{де K - константа рiвноваги реакцiї.}

В умовах рівноваги константа реакції є постійною величиною при даних температурі та тиску.

При стандартному тиску 0,1 МПа рівняння набудуть вигляду

_{Використовуючи десятковi логарифми шляхом простих перетворень отримаємо для любих температур i тискiв}

_{Умовно приймаючи V незалежним вiд температури i тиску, отримуємо}

_{для любих температур i тиску 1 бар}

Розрахувавши константу рiвноваги реакцiї ми можемо оцiнити вплив змiн активностей компонентiв системи на напрямок протiкання реакцiї мiнералоутворення

Розрахунок буферних реакцій. Константа рівноваги реакції А_тв=В_тв+С_газ визначається рівнянням

звідси

В рівноважних умовах при постійних температурі і тиску фугітивність газу (константа рівноваги реакції) має чітко фіксоване значення.

Реакції, в ході яких фугітивність газової фази підтримується на постійному рівні називаються буферними.

Приклад. Розрахувати рівноважні фугітивності кисню для реакції при різних температурах і тиску 1000 бар.

1. За табульованими значеннями ізобарних потенціалів гематиту, магнетиту і кисню розраховуєммо за рівнянням (16) значення ΔG_Т реакції при різних температурах і тиску 1 бар. Знайдені значення ΔG_Т реакції для різних температур записуються в табл

2.Розраховуємо зміну об’єму твердих фаз для даної реакції за рівнянням . Кал/бар.

3.Оскільки для цієї реакції , то Звідси за рівнянням (36) визначаємо логарифми фугітивності кисню для реакції при різних температурах і тиску 1000 бар. Хід розрахунків зрозумілий з табл.

4. За даними табл. будуємо діаграму в координатах (рис.) лінія на якій відповідає багатоваріантній рівновазі гематиту і магнетиту за заданими значеннями загального тиску. При збільшенні фугітивності кисню буде стійка більш окислена фаза (гематит), а нижче – більш відновлена фаза (магнетит).

Основний вплив на фугітивність кисню, який знаходиться в рівновазі з гематитом і магнетитом, здійснює температура. Останнє зумовлено малим об’ємним ефектом даної реакції.

Слід відмітити, що в подібних буферних реакціях фугітивність рівноважної газової фази не залежить від кількісного співвідношення твердих фаз.