3.3. Принадлежность точки и прямой плоскости

Точка принадлежит плоскости, если она принадлежит какой-либо прямой этой плоскости.

Прямая принадлежит плоскости, если две ее точки принадлежат плоскости.

Эти два вполне очевидных предложения часто называют условиями принадлежности точки и прямой плоскости.

На рис. 3.6 плоскость общего положения задана треугольником АВС. Точки А, В, С принадлежат этой плоскости, так как являются вершинами треугольника из этой плоскости. Прямые (АВ), (ВС), (АС) принадлежат плоскости, так как по две их точки принадлежат плоскости. Точка N принадлежит (AC), D принадлежит (AB), E принадлежит (CD) и, значит, точки N и E принадлежат плоскости (ABC), тогда прямая (NE) принадлежит плоскости (ABC).

Если задана одна проекция точки L, например L₂, и известно, что точка L принадлежит плоскости (ABC), то для нахождения второй проекции L₁ последовательно находим (A₂L₂), K₂, (A₁K₁), L₁.

Если условие принадлежности точки плоскости нарушено, то точка не принадлежит плоскости. На рис. 3.6 точка R не принадлежит плоскости (ABC), так как R₂ принадлежит (F₂K₂), а R₁ не принадлежит (A₁K₁).

На рис. 3.7 приведен комплексный чертеж горизонтально проецирующей плоскости (CDE). Точки K и P принадлежат этой плоскости, так как P₁ и K₁ принадлежат прямой (D₁C₁), являющейся горизонтальной проекцией плоскости (CDE). Точка N не принадлежит плоскости, так как N₁ не принадлежит (D₁C₁).

Рис.2.5

Рис.2.6

Все точки плоскости (CDE) проецируются на П₁ в прямую (D₁C₁). Это следует из того, что плоскость (CDE)  П₁. В этом же можно убедиться, если проделать для точки P (или любой

другой точки) построения, которые были сделаны для точки L (рис. 3.6). Точка P₁ попадет на прямую (D₁C₁). Таким образом, для того, чтобы определить принадлежность точки горизонтально проецирующей плоскости, фронтальная проекция (C₂D₂E₂) не нужна. Поэтому в дальнейшем проецирующие плоскости будут задаваться только одной проекцией (прямой линией). На рис. 3.7 показана фронтально проецирующая плоскость , заданная фронтальной проекцией ₂, а также точки A   и B  .

Взаимное положение точки и плоскости сводится к принадлежности или не принадлежности точки плоскости.

Метод замены плоскостей проекций

Метод замены плоскостей проекций состоит в том, что вместо одной из плоскостей проекций вводится новая плоскость, перпендикулярная к другой плоскости проекций. На рис. 2.6 показана пространственная схема получения комплексного чертежа точки А в системе (П₁П₂). Точки А₁ и А₂ – горизонтальная и фронтальная проекции точки А, АА₁А_xА₂ – прямоугольник, плоскость которого перпендикулярна оси x (рис. 2.7).

Новая плоскость П₄ перпендикулярна П₁. При проецировании точки А на П₄ получим новую проекцию А₄, фигура АА₁А₁₄А₄ – прямоугольник, плоскость которого перпендикулярна новой оси x₁₄ = П₄  П₁. Для получения комплексного чертежа будем рассматривать фигуры, расположенные в плоскостях проекций. Поворотом вокруг оси x₁₄ совместим П₄ с П₁, затем поворотом вокруг оси x совместим П₁ (и П₄) с П₂ (на рис. 2.6 направления движения плоскостей П₄ и П₁ показаны штриховыми линиями со стрелками). Полученный чертеж приведен на рис. 2.7. Прямые углы на рис. 2.7 и 2.8 помечены дугой с точкой, равные отрезки помечены двумя штрихами (противоположные стороны прямоугольников на рис. 2.6). От комплексного чертежа точки А в системе (П₁П₂) перешли к комплексному чертежу точки А в системе (П₁П₄), заменили плоскость П₂ на плоскость П₄, заменили А₂ на А₄.

На основе этих построений сформулируем правило замены плоскостей проекций (правило получения новой проекции). Через незаменяемую проекцию проводим новую линию проекционной связи перпендикулярно новой оси, затем от новой оси по линии проекционной связи откладываем отрезок, длина которого равна расстоянию от заменяемой проекции до старой оси, полученная при этом точка и есть новая проекция. Направление новой оси будем брать произвольно. Новое начало координат указывать не будем.

Н

Рис.2.8

а рис. 2.8 показан переход от комплексного чертежа в системе (П₁П₂) к комплексному чертежу в системе (П₂П₄), а затем еще один переход к комплексному чертежу в системе (П₄П₅). Вместо плоскости П₁ введена плоскость П₄, перпендикулярная П₂, затем вместо П₂ введена плоскость П₅, перпендикулярная П₄. Используя правило замены плоскостей проекций, можно выполнить любое количество замен плоскостей проекций.

Лекция №3

ИЗОБРАЖЕНИЯ – ВИДЫ, РАЗРЕЗЫ, СЕЧЕНИЯ

Правила изображения предметов на чертежах всех отраслей промышленности устанавливает стандарт 2.305-68

Изображения делятся на виды, разрезы, сечения

Вид – изображение обращенной к наблюдателю видимой части поверхности предмета [11, п.1.5].

Изображения предметов должны выполняться по методу прямоугольного проецирования. При этом предмет предполагается расположенным между наблюдателем и соответствующей плоскостью проекций.

За основные плоскости проекций принимают шесть граней куба; грани совмещают с плоскостью 1, грань «6» допускается располагать рядом с гранью «4» (рис.2.9).

Рис.2.9

1. Устанавливаются следующие названия видов, получаемых на основных плоскостях проекций (основные виды, рис. 2.9 и 2.10):

1 – вид спереди (главный вид); на фронтальной плоскости проекций П2;

2 – вид сверху; на горизонтальной плоскости проекций П1;

3 – вид слева; на профильной плоскости проекций П3;

4 – вид справа;

5 – вид снизу;

6 – вид сзади.

Все виды (проекции предмета) находятся в проекционной связи (7 – линии связи (рис.21 и 23)). В этом случае названия видов на чертежах надписывать не следует, за исключением случая, предусмотренного в п. 2.

2. Если виды сверху, слева, справа, снизу, сзади смещены относительно главного изображения (изображено на фронтальной плоскости проекций), то они должны быть отмечены на чертеже надписью по типу «А» (рис. 2.11 и 2.12 в и г).

Направление взгляда должно быть указано стрелкой, обозначенной прописной буквой.

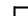
Рис. 2.11

Чертежи оформляют также, если перечисленные виды отделены от главного изображения другими изображениями или расположены не на одном листе с ним.

Когда отсутствует изображение, на котором может быть показано направление взгляда, название вида надписывают.

Дополнительные виды

1. Если какую-либо часть предмета невозможно показать из перечисленных в п. 2.12 видов без искажения формы и размеров, то применяют дополнительные виды, получаемые на плоскостях, не параллельных основным плоскостям проекций (рис. 2.12 а и б).

2. Дополнительный вид должен быть отмечен на чертеже надписью типа «А», а у связанного с дополнительным видом изображения предмета должна быть поставлена стрелка, указывающая направление взгляда, с соответствующим буквенным обозначением .

а) б)

в) г)

Рис. 2.12

Когда дополнительный вид расположен в непосредственной проекционной связи с соответствующим изображением, стрелку и надпись над видом не наносят (рис. 2.13).

Рис. 2.13

Д ополнительный вид допускается повернуть, но с сохранением , как правило, положения, принятого для данного предмета на главном изображении; при этом к надписи должен быть добавлен знак

Местные виды

Изображение отдельного, ограниченного места поверхности предмета называется местным видом.

Местный вид может быть ограничен линией обрыва, по возможности в наименьшем размере (рис. 26в), или не ограничен.

Отдельно расположенный местный вид должен быть отмечен на чертеже подобно дополнительному виду (рис. 2.12б).

РАЗРЕЗЫ

Правила изображения и обозначения разрезов устанавливает стандарт [11].

Разрез – изображение предмета, мысленно рассеченного одной или несколькими плоскостями, при этом мысленное рассечение предмета относится только к данному разрезу и не влечет за собой изменения других изображений того же предмета. На разрезе показывается то, что получается в секущей плоскости и что расположено за ней.

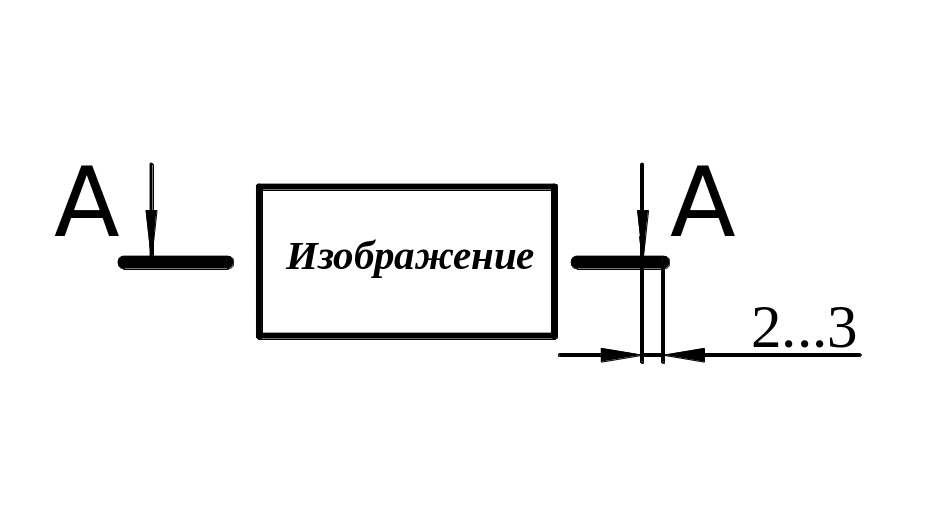Положение секущей плоскости указываются на чертеже линией сечения. Для линии сечения должна применяться разомкнутая линия.

Рис. 2.13

Начальные и конечные штрихи не должны пересекать контур соответствующего изображения. Перпендикулярно начальному и конечному штрихам наносят стрелки, указывающие направление взгляда. Стрелки отстоят на 2…3 мм от конца штриха (рис. 2.13). У начала и конца линии сечения ставят одну и ту же прописную букву русского алфавита. Буквы наносят около стрелок, указывающих направление взгляда с внешней стороны. Над разрезом располагают надпись по типу А-А.

Простые разрезы

В зависимости от положения секущей плоскости относительно горизонтальной плоскости проекций разрезы делятся на три типа:

1) горизонтальные – секущая плоскость параллельна горизонтальной плоскости проекций (рис. 2.14);

2) вертикальные – секущая плоскость перпендикулярна горизонтальной плоскости проекций (рис. 2.15). Вертикальный разрез называется фронтальным (рис. 2.15), если секущая плоскость параллельна фронтальной плоскости проекций, и профильным, если секущая плоскость параллельна профильной плоскости проекций;

3) наклонные – секущая плоскость составляет с горизонтальной плоскостью проекций угол, отличный от прямого.

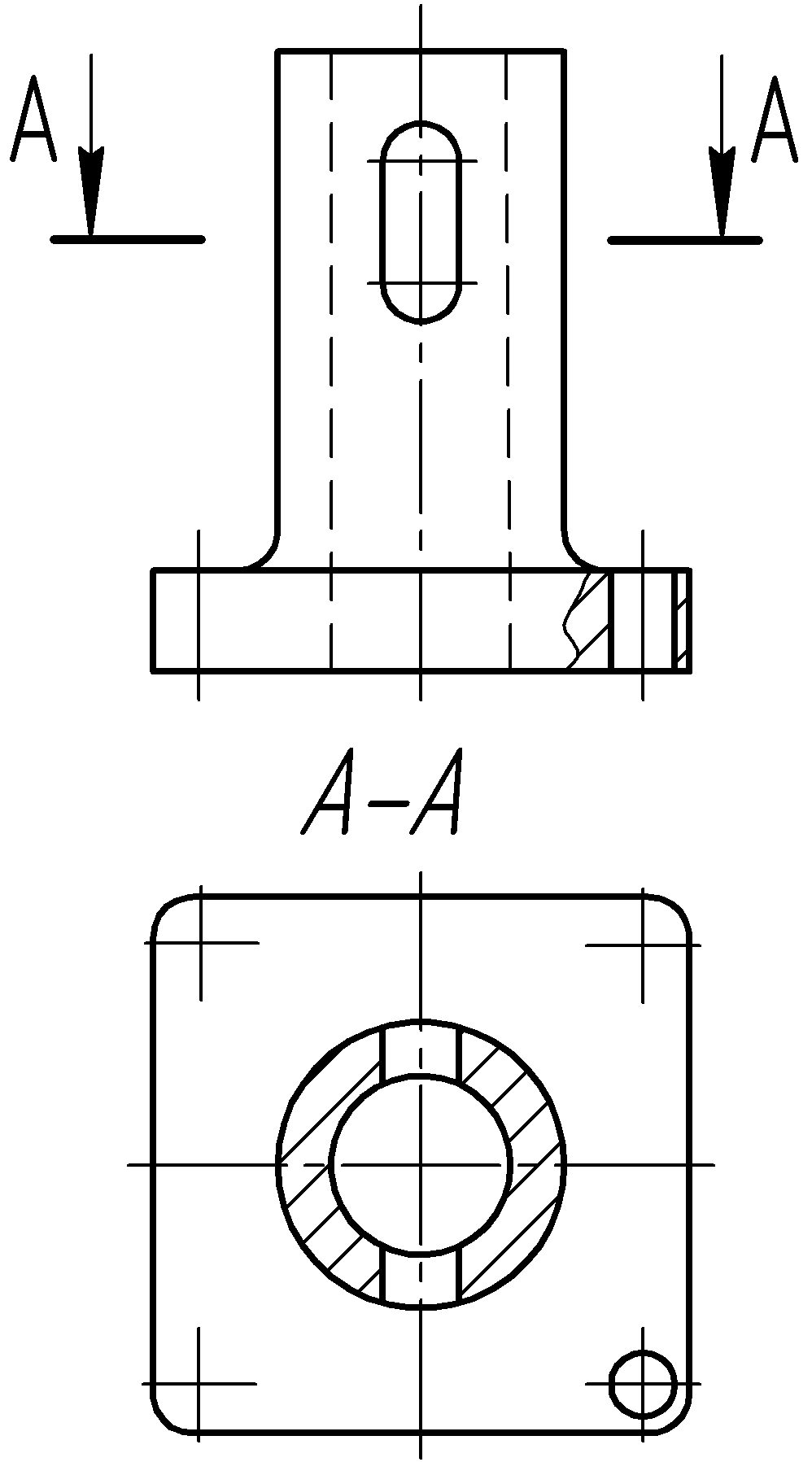
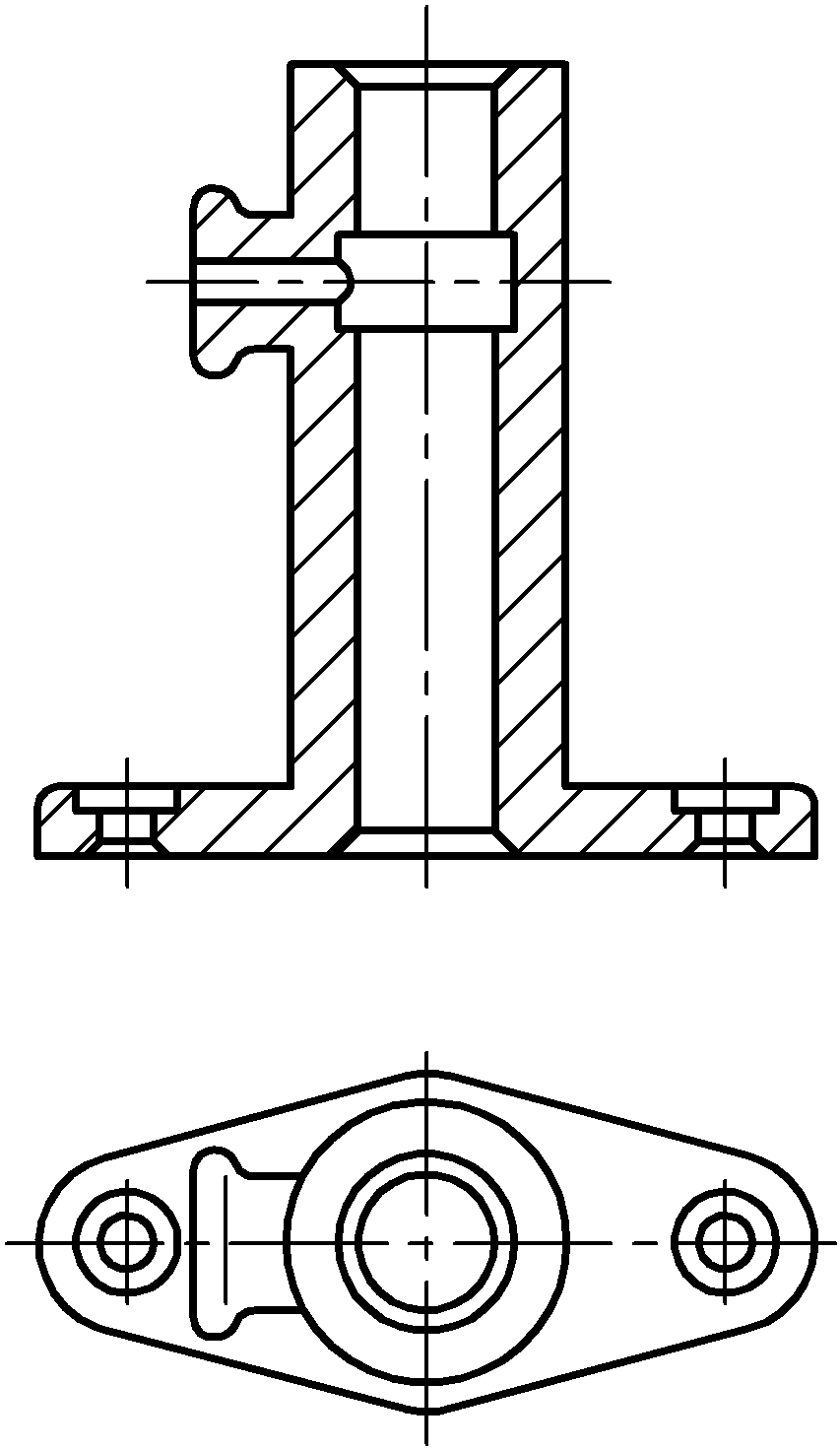
Рис. 2.14 Рис. 2.15

Простой разрез на чертеже не обозначается, если выполняются одновременно два следующих условия:

1) секущая плоскость совпадает с плоскостью симметрии детали;

2) в проекционной связи на месте основного вида горизонтальный разрез – на месте вида сверху, фронтальный – вида спереди, профильный – вида слева (рис. 2.15). Если не выполняется хотя бы одно из этих условий, то разрез обозначается согласно [12], как показано на рис. 2.14.

Н аклонный разрез должен строиться и располагаться в соответствии с направлением, указанным стрелками. Такой разрез допускается располагать на любом месте чертежа, с поворотом и добавлением к надписи А-А знака (рис.2.16).

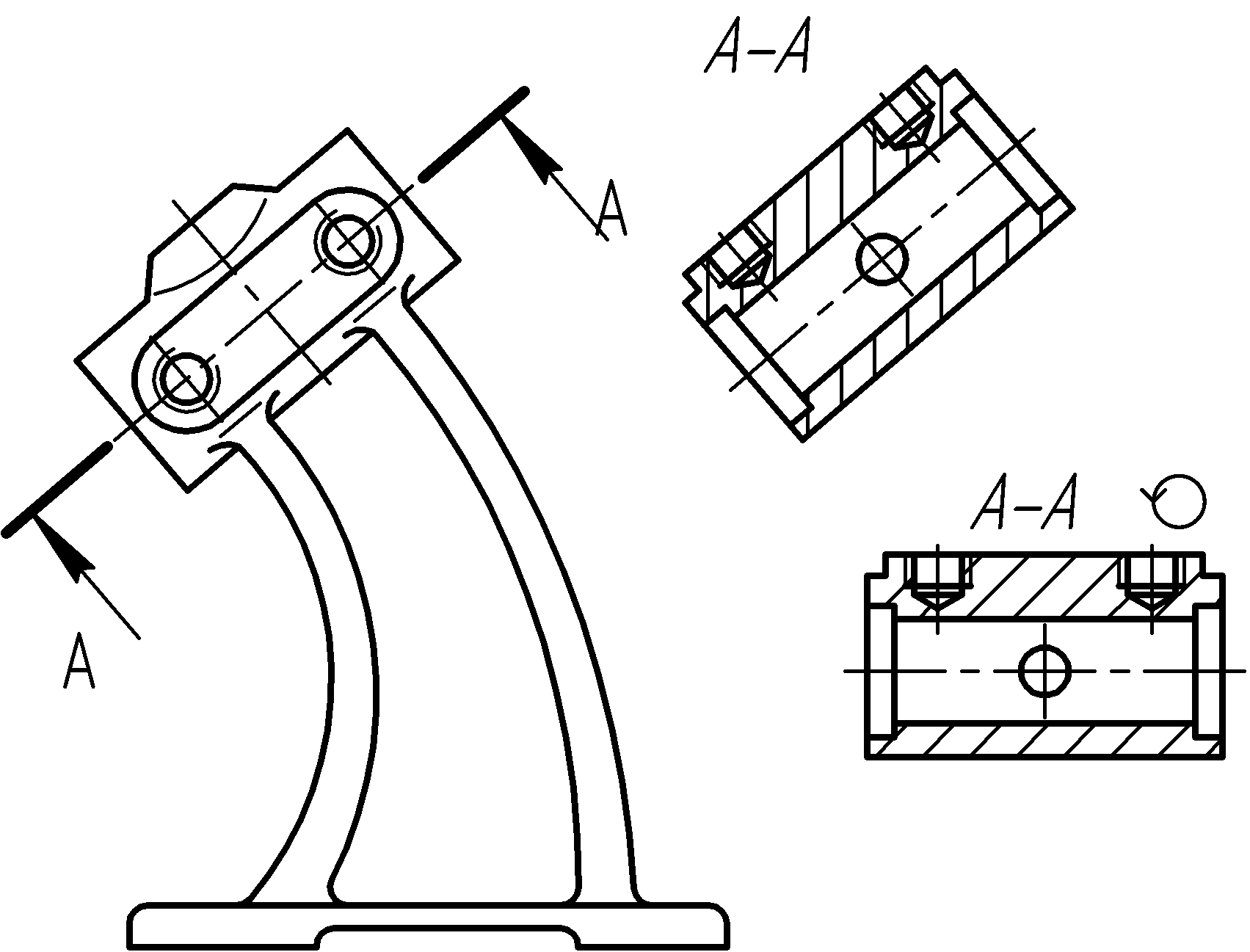
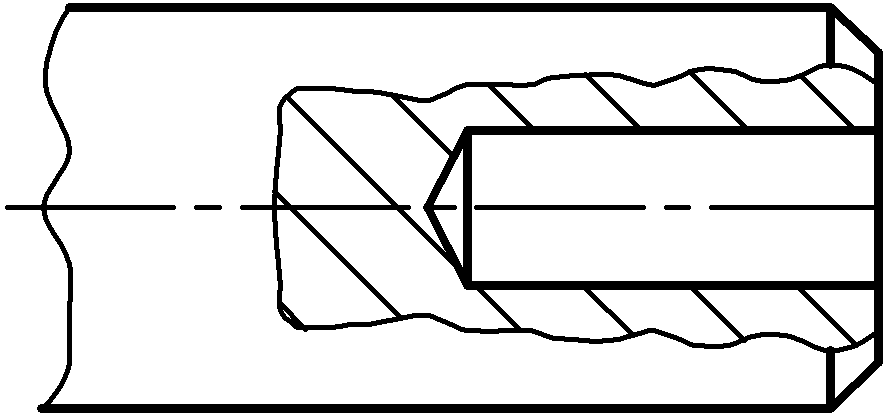
Рис. 2.17

Рис. 2.16

Местный разрез – разрез, служащий для выяснения устройства детали в отдельном узкоограниченном месте. Граница местного разреза проводится сплошной волнистой линией.

Рекомендуется, чтобы эта линия не совпадала с линиями контура изображения детали (рис. 2.17)

Если предмет симметричный, то следует соединять половину вида с половиной соответствующего разреза. Это делается с целью сокращения графической работы и улучшения чтения чертежа. Границей между видом и разрезом служит осевая линия симметрии (рис. 2.18).

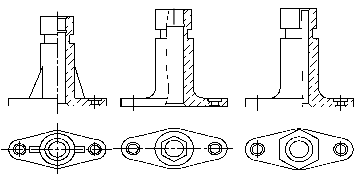
Рис. 90 Рис. 91 Рис. 92

Рис. 2.18

На рис. показана деталь, у которой с осью симметрии на главном изображении совпала проекция внутреннего ребра. В этом случае соединяют меньшую часть вида с большей частью соответствующего разреза, а границей между ними служит сплошная волнистая линия (толщина ее S/2-S/3). Если с осью симметрии совпадает наружное ребро, то соединяют большую часть вида с меньшей частью соответствующего разреза.

Сложные разрезы

Ступенчатые разрезы

Сложный разрез называется ступенчатым, если секущие плоскости параллельны (например, ступенчатый горизонтальный разрез А-А, рис. 2.19; ступенчатый фронтальный разрез Б-Б, рис. 2.20).