2.1.3. Интерполирование полиномами

в

общем виде уравнение полинома

имея n значений x b y можно определить все значения коэффициентов и, соответственно любую промежуточную точку.

Пусть (x₁,y₁), (x₂,y₂), ..., (x_n,y_n) – последовательность точек, заданных на плоскости, причём x_i  x_j , при ij. Формулу интерполяционного полинома (n-1)- степени можно представить в виде

(1)

Основным недостатком интерполирования с помощью полиномов является значительное отклонение кривой между точками – узлами интерполирования. (рис)

Уравнение полинома (1) представляет интерполяционную формулу Лагранжа. Для решения задач КГ более подходит параметрическая формула

. (2)

В

(3)

случае, когда к заданным точкам добавляются новые точки интерполяции, рекомендуется использовать интерполяционный полином Ньютона

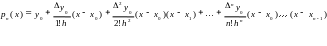
где h- шаг интерполяции;

y_i =y_i+1- y_i (i=0,1,2,…) – конечная разность (11)

В ажным преимуществом этого полинома является то, что добавление новых точек интерполяции приводит только к добавлению новых членов в уравнении (3), предыдущие вычисления остаются без изменений.

В случае, когда заданы не только функции, но и касательные в заданных точках, применяются интерполяционные полиномы Эрмита, являющиеся обобщением интерполяционных полиномов Лагранжа

(4)

где – полином Лагранжа.

Полиномиальную интерполяцию имеет смысл применять лишь для небольшого числа точек (не более пятнадцати) из-за того, что с числом точек растёт степень полинома и имеют место большие осцилляции в промежутках между заданными точками.

Недостатки полиномной кривой устранены в сплайнах и кривой Безье.

Сплайны

В сопромате описывается однородный брус, закрепленный в двух точках с приданием ему наклона в этих точках, т.е. заданных в них касательных. Напомню –касательная к кривой – это фактически первая производная. Кроме того задается непрерывность кривизны, а это вторая производная.

Зададим в параметрической форме сплайн кубической параболой, проходящей через две точки Р(0) и Р(1).

(1)

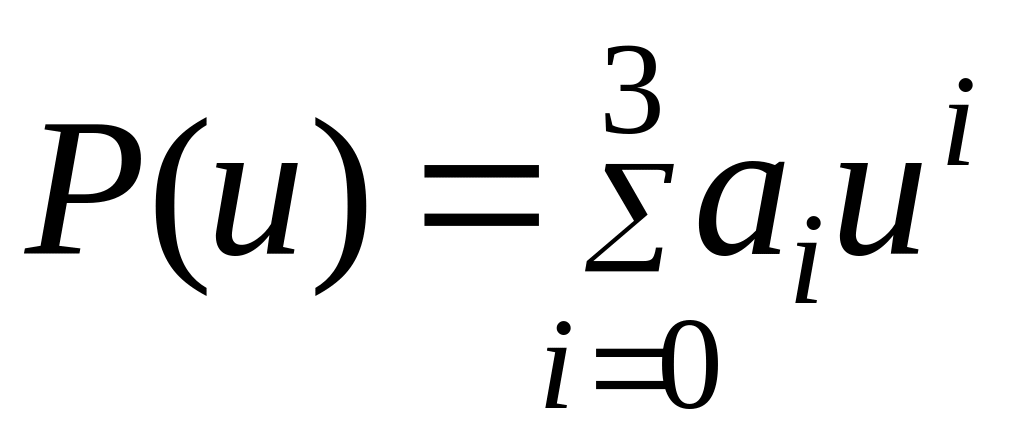
в точках 0 и 1 известны касательные, а значит первые производные:

и

отсюда есть условия для определения четырех коэффициентов

(2)

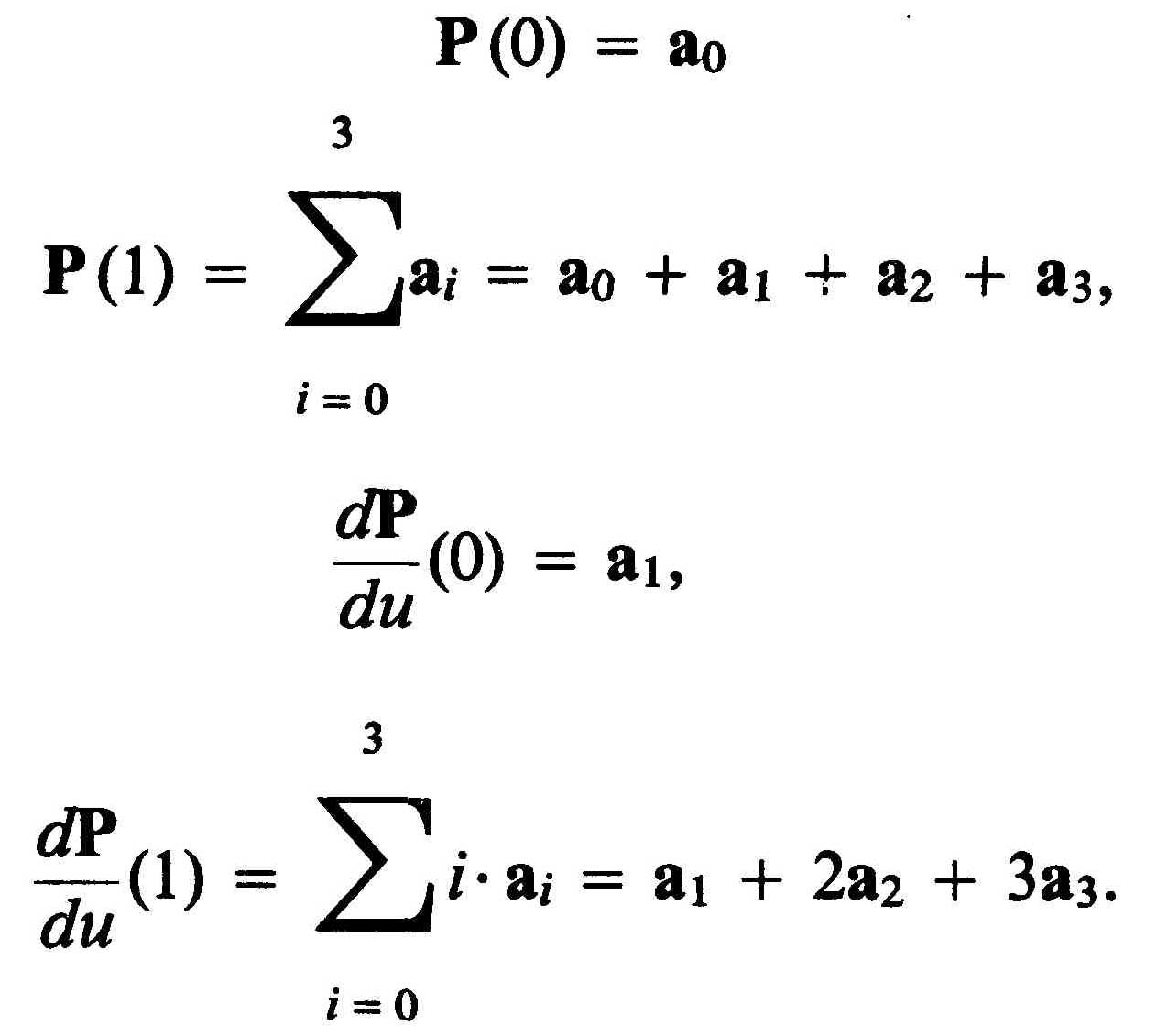
Из выражений (2) следует

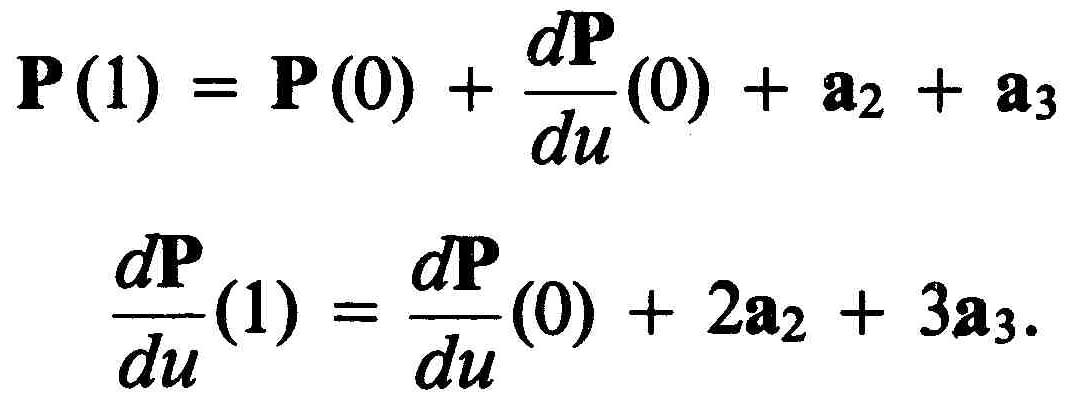
Отсюда можно вывести:

(3)

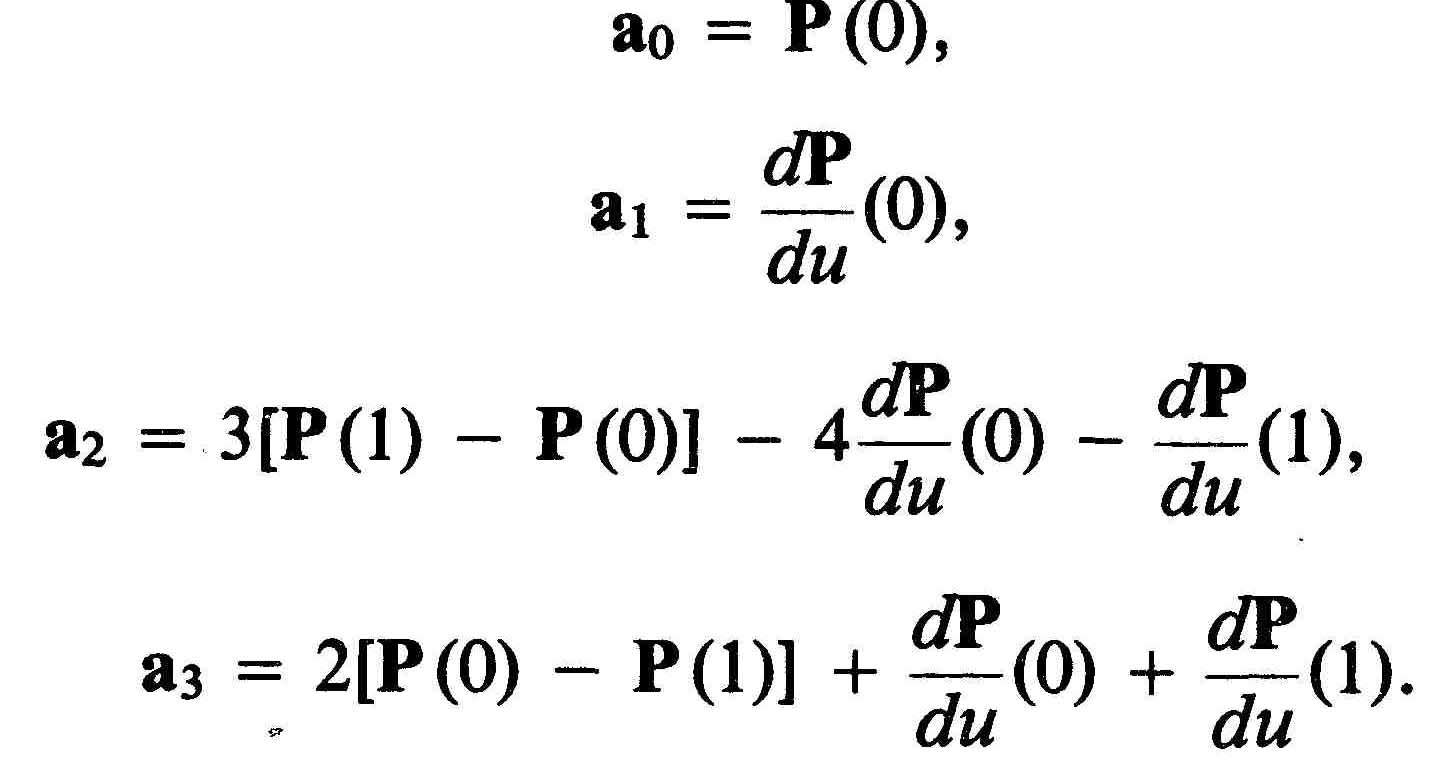
О

пределив кубическую параболу (рис.) между точками Р(0) и Р(1), для нахождения следующей дуги кривой между точками Р' (0) и Р' (1) необ­ ходимо в точках Р' (0) и Р(1) приравнять значения самой кривой и ее пер­вых производных и задать значение вектора —. Таким образом, шаг за за шагом определяется последовательность дуг кубической кривой, соеди­няющей точки Р, Р', ... , Рп и имеющей непрерывные касательные в этих точках.

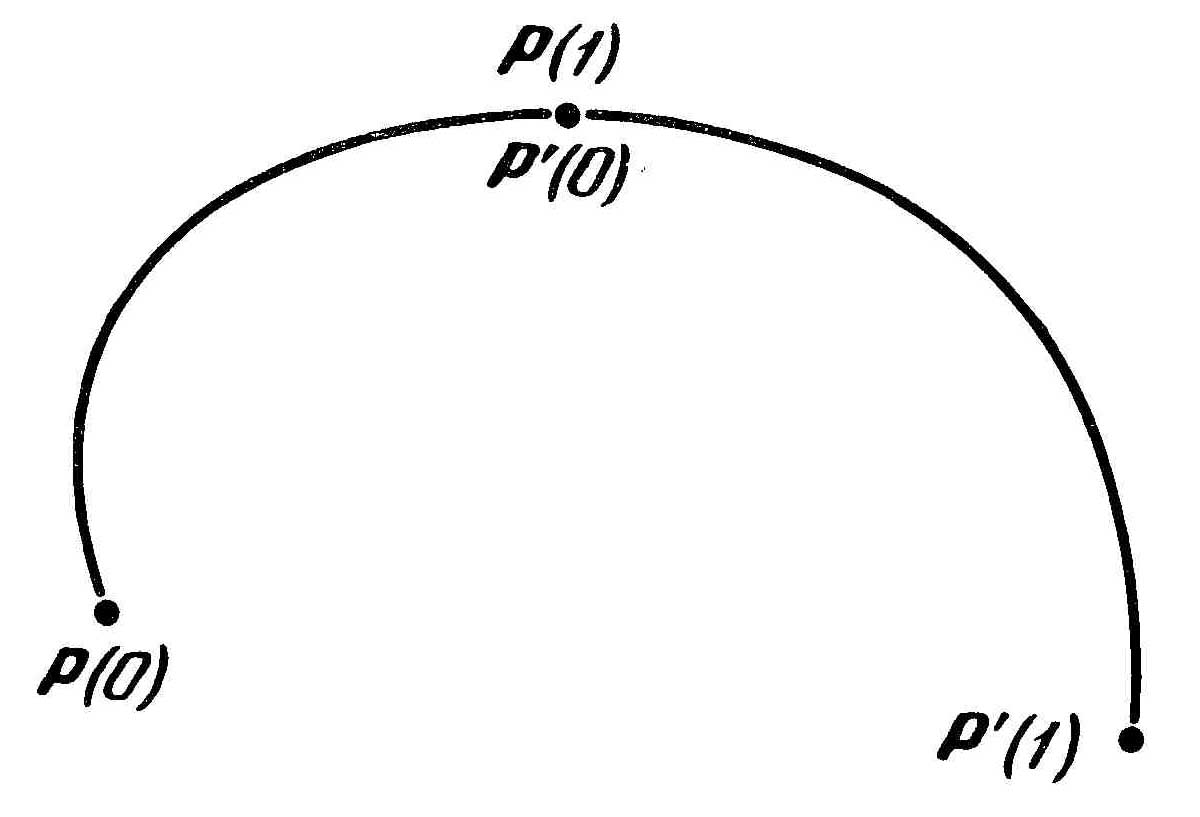
Хотя теоретически оба метода эквивалентны друг другу, тем не менее следует согласиться с тем, что управлять формой кривой проще, задавая значения первых производных на ее концах, а не значения второй произ­водной в начальной точке.

кривые Безье

Сегмент кривой Безье (Bezier) третьего порядка описывается положе­нием четырех точек. Две из них являются опорными (узлами кривой): начальная точка Р₀ (х₀, у₀) и конечная точка Р₃ (х₃, у₃). Точки Р₁ (x_l y) и Р₂ (х₂, у₂), определяющие положение касательных относительно от­резка, называют управляющими (1). Метод построения кривой Безье основан на использовании пары касательных (управляющих линий), проведенных к сегменту кривой в его окончаниях. На форму кривой влияют угол наклона касательной и длина ее отрезка (рис. 255).

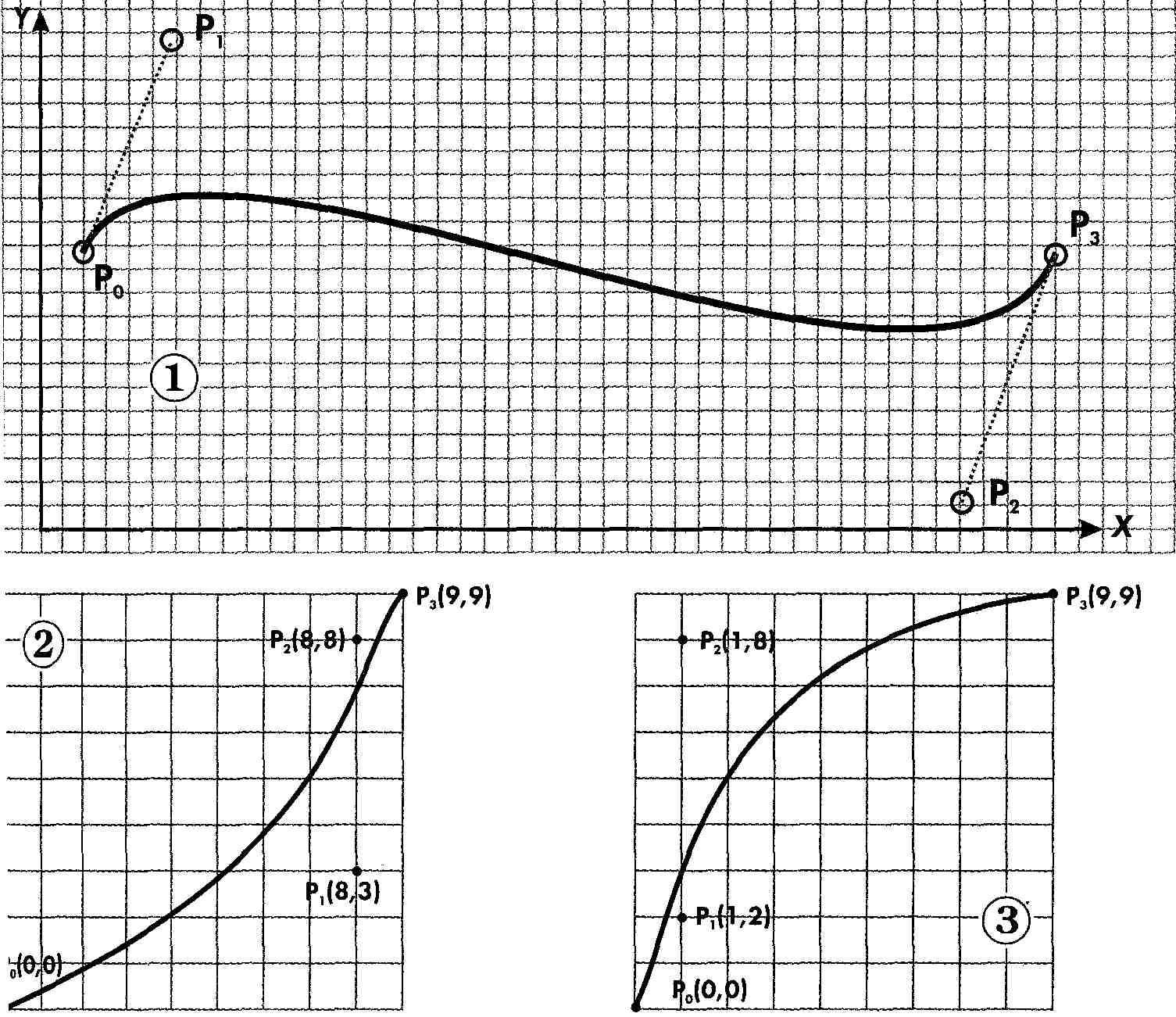
Параметрическое уравнение Безье описывает положение точек и, тем самым, форму кривой. Уравнение решают относительно параметра t, принимающего значения от 0 (в начальной точке) до 1 (в конечной точ­ке). При построении сегмента кривой Безье на плоскости рассчитыва­ют координаты x и у (для четырех точек, из них двух управляющих):

R(t) = Р₀(1 - t)³ + Р₁t(1 - t)2 + P₂t²(l - 1) + P₃t³, где 0 < t <1;

Значение t определяет степень влияния точек на форму кривой (2, 3). Например, при t = 0,333 наибольший «вес» приобретает точка P₁ (x_v y), а при t = 0,666 — точка Р₂ (х₂, у₂). Из приведенных уравнений вытека­ет, что кривая может проходить лишь через начальную и конечную опорные точки сегмента (Р₀, Р₃). Тем самым достигаются простота опи­сания и стабильность кривой Безье.

Свойство кривой Безье

Кривые Безье обладают рядом свойств, определяющих возможность их использования в векторной графике. С геометрической точки зре­ния, производной кривой Безье будет другая кривая Безье, векторы управляющих точек которой определяются вычислением разностей векторов управляющих точек исходной кривой.

Основные свойства кривой Безье:

• непрерывность заполнения сегмента между начальной и конечной точками;

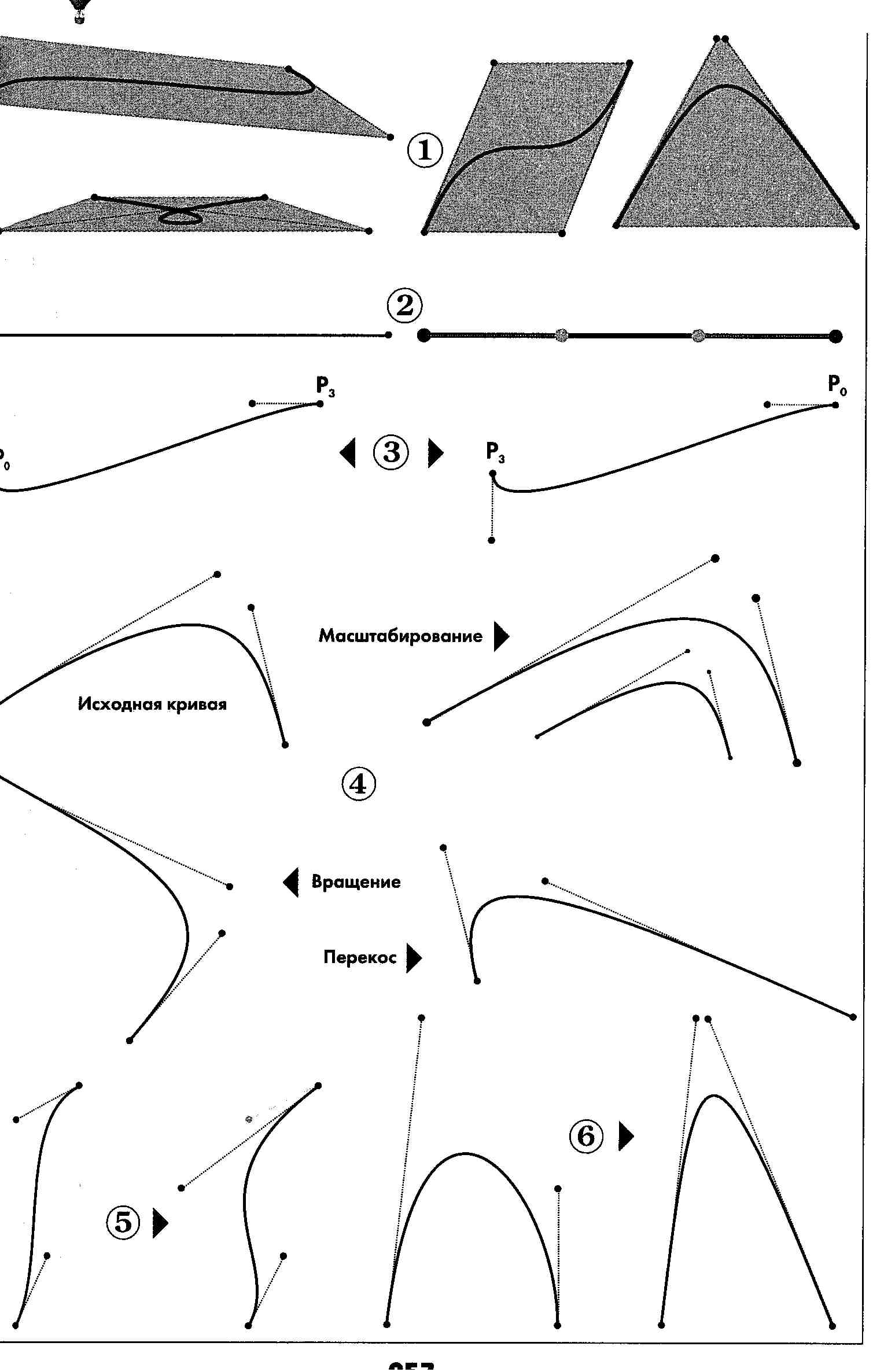
• кривая всегда располагается внутри фигуры, образованной линиями, соединяющими контрольные точки (1);

• при наличии только двух контрольных точек сегмент представляет собой прямую линию (2);

• прямая линия образуется при коллинеарном (на одной прямой) размещении управляющих точек (2);

• к ривая Безье симметрична, то есть обмен местами между начальной и конечной точками (изменение направления траектории) не влияет на форму кривой (3);

• масштабирование и изменение пропорций кривой Безье не нарушает ее стабильности, так как она с математической точки зрения «аффинно инвариантна» (4);

• изменение координат хотя бы одной из точек ведет к изменению формы всей кривой Безье (5);

• степень кривой всегда на одну ступень ниже числа контрольных точек. То есть при трех контрольных точках форма кривой — парабола;

• размещение дополнительных контрольных точек вблизи одной позиции увеличивает ее «вес» и приводит к приближению траектории кривой к данной позиции (6);

• окружность не может быть описана параметрическим уравнением кривой Безье;

• невозможно создать параллельные кривые Безье, за исключением тривиальных случаев (прямые линии и совпадающие кривые).

• Метод кунса

• По данному методу на участке от i-той точки принятой за начальную t= (0) до i+1-конечной t= (1) происходит плавный переход от одних параметров (например дуги окружности по предыдущим точкам до i- ой точки) к параметрам i+1 и далее.

Функции перехода: