Математические основы векторной графики

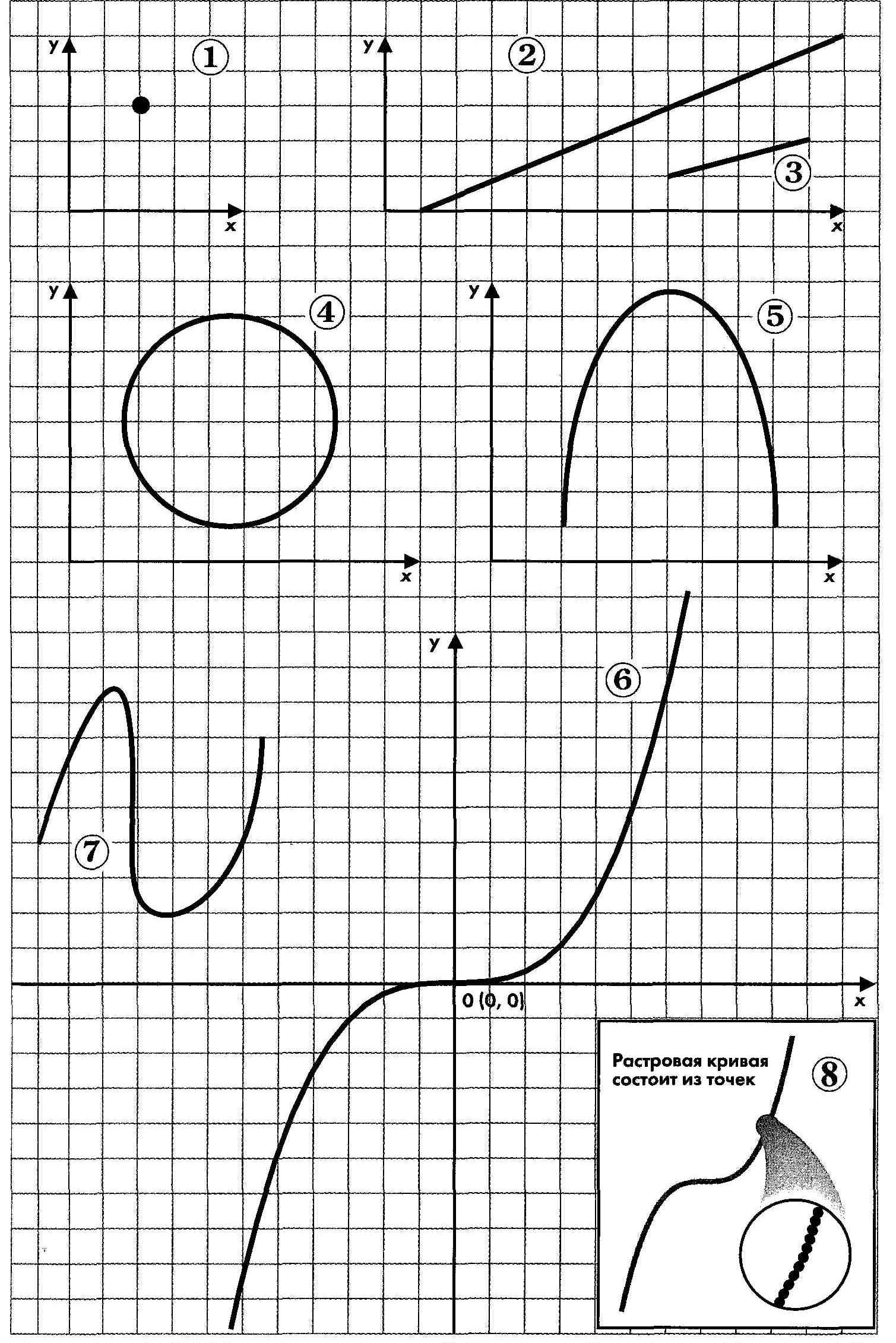
Рассмотрим способы представления объектов в векторной графике

Точка. Этот объект на плоскости представляется двумя числами (х, у), указывающими его положение относительно начала координат (1).

Прямая линия. Ей соответствует уравнение у = kx + b. Указав пара­метры k и b, всегда можно отобразить бесконечную прямую линию в известной системе координат, то есть для задания прямой достаточно двух параметров (2).

Отрезок прямой. Он отличается тем, что требует для описания еще двух параметров — например, координат х_: и х₂ начала и конца от­резка (3).

. Конструирование кривых

В компьютерной графике при вычерчивании изображений возникают задачи построения кривых по точкам. В отечественной литературе эти задачи называют конструированием кривых.

Основные принципы конструирования кривых:

а) кривая должна быть кусочно-составной;

б) иметься возможность управления формой кривой;

в) увеличение числа сегментов кривой не должно нарушать гладкость кривой;

г) использование минимального количества параметров для математических моделей, описывающих кривые;

д) возможность преобразования изображения;

е) возможность описания кривых с касательными, параллельными осями координат;

ж) обеспечения простого с точки зрения реализации вычислений способа определение произвольной точки кривой.

В описании кривых в КГ возможны два подхода:

1. задание кривой уравнением;

б) описание приближенными методами: интерполяции и аппроксимации.

Отыскание кривой, проходящей через заданное число точек, составляет задачу интерполирования, а отыскание кривой, проходящей вблизи заданных точек – задачу аппроксимации.

Кривая второго порядка. К этому классу кривых относятся парабо­лы, гиперболы, эллипсы, окружности, то есть все линии, уравнения которых содержат степени не выше второй. Кривая второго порядка не имеет точек перегиба. Прямые линии являются всего лишь част­ным случаем кривых второго порядка. Формула кривой второго по­рядка в общем виде выглядет, так:

х² + a₁у² + а₂ху + а₃х + а₄у + а₅ = О.

Таким образом, для описания бесконечной кривой второго порядка до­статочно пяти параметров. Если требуется построить отрезок кривой, понадобятся еще два параметра (5).

Кривая третьего порядка. Отличие этих кривых от кривых второго порядка состоит в возможном наличии точки перегиба. Например, гра­фик функции у = х3 имеет точку перегиба в начале координат. Именно эта особенность позволяет сделать кривые третьего порядка основой отображения природных объектов в векторной графике. Линии изги­ба человеческого тела, контуры пересеченной местности, очертания растений весьма близки к кривым третьего порядка. Все кривые вто­рого порядка, в том числе прямые линии, являются частными случая­ми кривых третьего порядка.

В общем случае уравнение кривой третьего порядка можно записать так:

х³ + а_гу³ + а₂х²у + а₃ху² + а₄х² + а₅у² + а₆ху + а₇х + а₈у + а₉ = О

Таким образом, кривая третьего порядка описывается девятью пара­метрами (6). Описание ее отрезка потребует на два параметра больше (7). Несмотря на кажущуюся сложность описания кривой третьего по­рядка, ее код занимает в файле несравнимо меньше места, чем код аналогичной кривой, но созданной из точек (растровой). Для растро­вой линии дают описание положения и цвета каждой точки (8).