1.3. Обозначение резьб

Так как все резьбы на чертеже изображают одинаково, то тип резьбы и ее основные размеры указывают на чертежах особой надписью, называемой обозначением резьбы. Примеры условных обозначений резьб общего назначения приведены в табл.

Таблица

Стандартные резьбы

Изображение	Резьба	Обозначение	Примеры
	Метрическая: с крупным шагом с мелким шагом многозаходная	М d M d × P M d × Ph (P)	М 24 M 24 × 2 M 24 × 4 (P2)
	Трапецеидальная: однозаходная многозаходная	Tr d × P Tr d × Ph (P)	Tr 36 × 6 Tr 60 × 8(P4)
	Упорная: однозаходная многозаходная	S d × P S d × Ph (P)	S 80 × 10 S 80 × 10(P5)
	Трубная цилиндрическая: класса А класса В	G d1 – A G d1 – B	G 1 1/2 – A G 1 1/2 – B

Однозаходные метрические резьбы при одном и том же наружном диаметре могут иметь несколько значений шага. Шаг с максимальным значением называется крупным, а остальные  мелкими. Выбор значения крупного шага производится из условия, чтобы угол подъема винтовой нитки был не больше 2º30^/. Крупный шаг в условном обозначении не указывается.

Левые резьбы обозначаются латинскими буквами LH, например, М201,5LH  резьба метрическая, диаметр 20 мм, шаг мелкий  1,5 мм, левая.

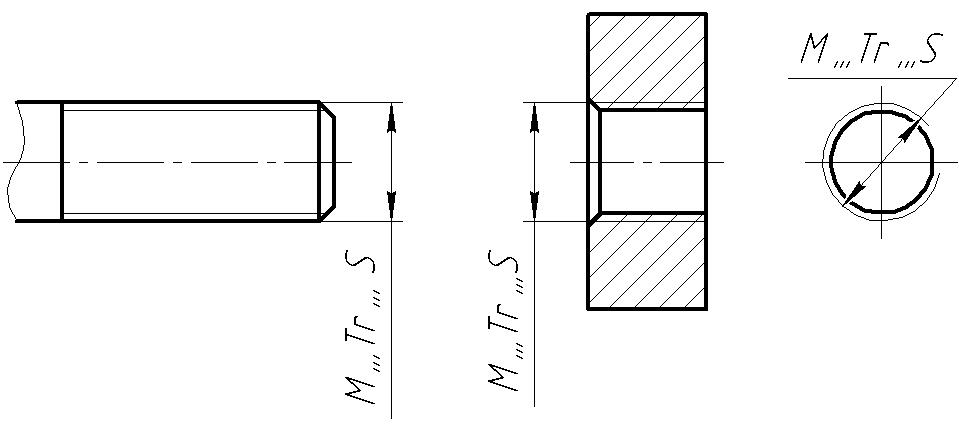
Нанесение обозначений резьб: метрической, трапецеидальной, упорной

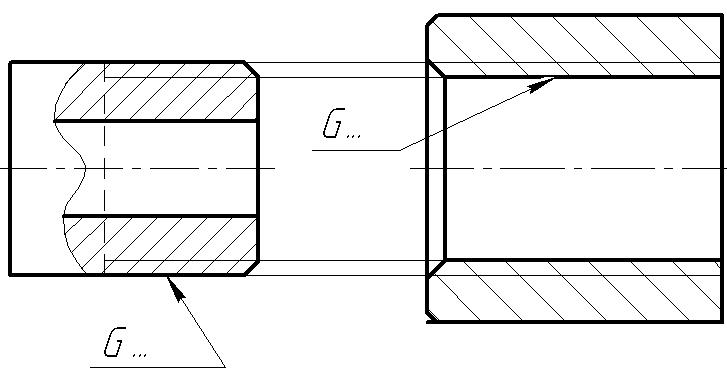
Нанесение обозначения трубной резьбы

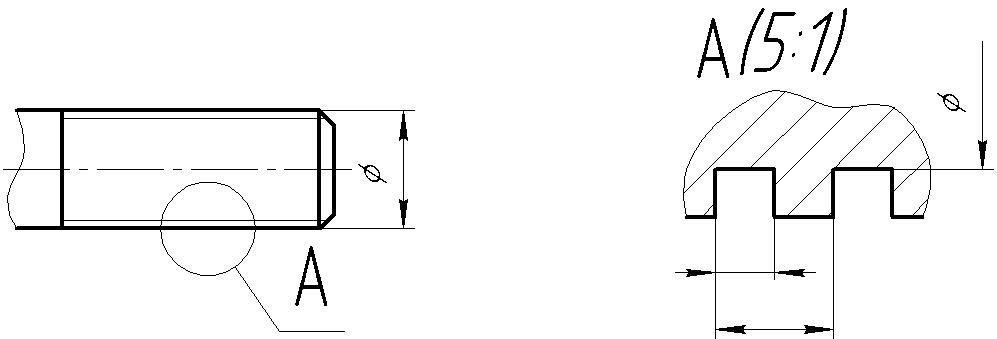
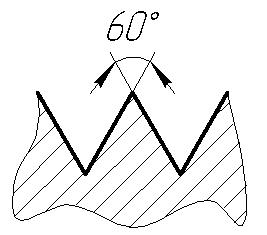
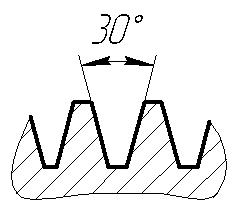
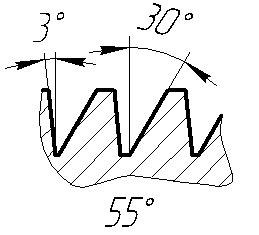
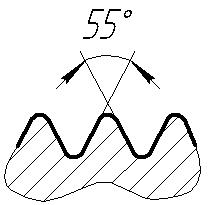
Изображение прямоугольной резьбы

На чертежах наносится обозначение резьб: метрической, трапецеидальной, упорной (рис. 4), трубной (рис. 5). Так как прямоугольная резьба нестандартная, то у нее нет обозначения. На чертеже эта резьба изображается так, как показано на рис. 6.

Лекция №8 основы компьютерной графики

Компьютерная графика может быть определена, как совокупность технических, программных, языковых средств и методов связи пользователя с ЭВМ на уровне зрительных образов при решении различных классов задач. Есть другое определение компьютерной графики, например под компьютерной графикой понимают совокупность средств и приёмов автоматизации подготовки, преобразования, хранения и воспроизведения графической информации с помощью ЭВМ.

Интерактивная компьютерная графика предполагает воспроизведение изображений в режиме диалога пользователя с ЭВМ в реальном масштабе времени.

Компьютерная графика необходима всем специалистам, особенно технического профиля. Это обусловлено, в первую очередь, красотой и эффективностью самой компьютерной графики. Кроме того, современные средства компьютерной графики представляют собой очень эффективный инструмент поддержки пространственно- образного мышления при выполнении научно- исследовательских, проектно- конструкторских и производственно- оформительских задач. И, наконец, в современном мире, где роль информации становится всё более важной, изображение превращается в её преобладающий носитель при общении. Спектр задач, решаемых компьютерной графикой, чрезвычайно широк: реклама, анимация, дизайн, компьютерные игры, полиграфия, автоматизация вычерчивания конструкторской документации, архитектура, бизнес и т.д.

При решении прикладных задач из выше перечисленных областей для связи "пользователь - ЭВМ " используют алфавитно-цифровые и графические представления данных. В компьютерной графике различают два класса графических данных: линейно- ориентированные представления, а также плоскостные, полутоновые и цветные представления. Первый класс охватывает чертежи, линии и соответственно вектора, которые строятся как последовательность точек. Ко второму классу относятся изображения, получаемые по известному из техники телевидения растровому методу, с помощью которого на экране воспроизводятся реальные объекты. Преобразование графических данных в графические изображения, может быть реализовано на основе векторной или растровой технологии. Информацию о графических данных необходимо хранить в компьютере. Средства задания и описания графических данных, создание структуры данных, изменения данных, доступ к данным, поиск нужной информации составляют информационное обеспечение компьютерной графики.