Приклад 38.

Акція приносить сталий прибуток 0,43 грн. щорічно. Яка її теперішня вартість, якщо діюча на ринку ставка по кредитах - 30% річних складних?

Розв’язок.

З (66) при R=0,43, і=0,3 знаходимо

грн.

9. Знаходження параметрів фінансових рент.

Часто виникає задача, знаючи А або S знайти один з параметрів ренти при відомих інших.

Якщо відомі А або S, термін ренти n та ставка і, то з (58), (62) знаходимо член ренти R:

(68)

Аналогічно використовуємо формули (65).

Якщо S, A, R, і відомі, то термін ренти n знаходимо з (58), (62) як вирази:

(69)

причому друга формула (69) має сенс при умові

Аі<R. (70)

Аналогічно вирази для n можна знайти з (65).

Приклад 39.

Підприємство вирішило створити фонд 1,5 млн. грн. за 3 роки. Якщо суму 986,2 тис. грн. розмістити під 15% у банку, то на кінець 3-го року мали б:

млн. грн.

Але одночасне забирання такої суми із господарчого обороту недоцільне. Тому віддається перевага щорічним рентним платежам. Маємо за (68) при і=15%, n=3 :

тис. грн.

Отже щорічний внесок 431,9 тис. грн. сформує фонд 1,5 млн. грн. на кінець 3-го року.

Приклад 40.

Сума інвестицій 100 тис. грн., віддача 25 тис. грн. щорічно. На борг нараховуються 20% річних. За який термін окупляться інвестиції?

Розв’язок.

Якщо теперішня величина надходжень більше інвестицій, то маємо їх окупність. Отже з (69) знаходимо:

р.

Інвестиції окупляться майже за 9 років. Якби взяли R=20 тис. грн., то інвестиції не окупилися би.

При визначенні доходності операцій з періодичними сплатами виникає задача знаходження ставки і ренти.

Щоб знайти ставку і треба розв’язати рівняння

або (71)

відносно і при відомих S, R, n, A.

Нелінійні рівняння (71) розв’язуються інтераційними методами Ньютона.

На практиці дуже зручно для розв’язку (71) користуватись програмами роботи з електронними таблицями, наприклад EXCEL 5.0. Для знаходження і використовується вбудована функція BHDOX (IRR) (див. EXCEL 5.0 для Windows, т. 2, c. 430-431).

Приклад 41.

За 7 років треба створити фонд 100 тис. грн. Для цього щорічно виділяють 10 тис. грн. Якою потрібна бути ставка, щоб фонд утворився?

Розв’язок.

Для і маємо рівняння

Звідси знаходимо і=11,709%.

Для знаходження наближеного розв’язку рівнянь (71) методом Ньютона, подамо ці рівняння у вигляді

(72)

Кожне з рівнянь (72) має вигляд

, (73)

де - функція, що задається лівою частиною (72).

Нехай якесь наближення до розв’язку (73). Тоді його уточнення за методом Ньютона має вигляд:

(74)

де - похідна функції .

Для рівнянь (72) формули (74) виглядають так:

(75)

(76)

Наближення знаходять звичайно з практичних міркувань.

Приклад 42.

За даними прикладу 41 знайдемо наближене значення і взявши За формулою (75) маємо:

Підставивши і у праву частину (75) отримаємо друге наближення і . Таким чином можна отримати розв’язок рівнянь (72) з будь-якою точністю.

10. Внутрішня норма доходності

Інвестиційний процес об’єднує два процеси: інвестиції (утворення виробничого об’екту, купівля цінних паперів,...) і послідовне отримання доходу.

Будь-який метод оцінки інвестиційних проектів зв’язаний з зведенням грошових величин до одного моменту часу.

Використовують такі характеристики інвестиційного процесу: чистий зведений доход, внутрішня норма доходності, термін окупності, рентабельність.

Зупинимось докладніше на ВНД - внутрішній нормі доходності, або внутрішній швидкості обороту (internal rate of return - IRR)

Представимо графічно інвестиційний процес:

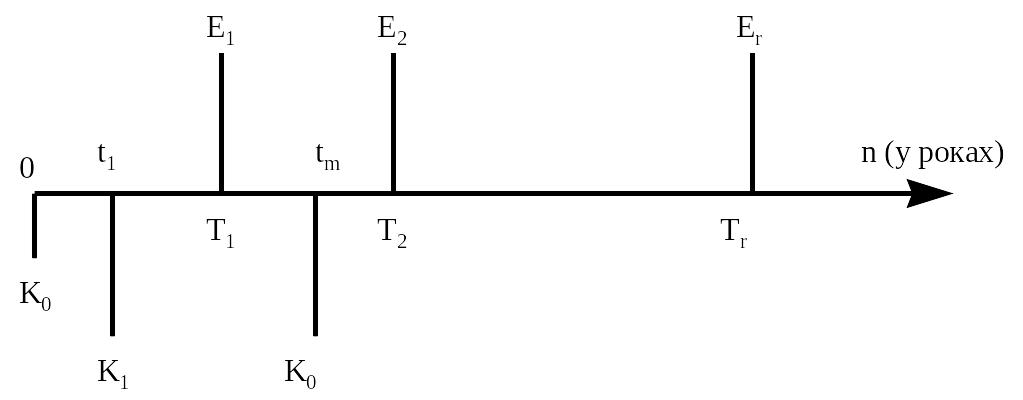
Інвестиції обсягів у моменти відкладаємо вниз і вважаємо від’ємним доходом. Доходи у моменти відкладаємо вгору.

Дисконтуємо усі доходи і інвестиції на початок відліку.

ВНД (IRR) - це відсоткова ставка, при якій зведена величина інвестицій дорівнюватиме зведеній величині доходів.

Тобто при нарахуванні на інвестиціі К відсотків за ставкою і=IRR отримуємо розподілений у часі доход.

Чим вище IRR . тим більша ефективність інвестицій.

Виходячи з графічного представлення інвестиційного процесу складемо рівняння для ВНД=і:

(77)

Рівняння (77) - нелінійне рівняння відносно і.

Розв’язується чисельними методами типу Ньютона з будь-якою точністю.

Для знаходження IRR використовується функція ВНДОХ (значення, прогноз), де у значення вводимо , а прогноз - наближенна оцінка IRR (див. EXCEL 5.0 для WINDOWS, т.2, с.430-431).

Якщо в найпростішому випадку інвестиції К - разові на початку і щорічний доход сталий Е, то можна використати формулу ренти. ВНД=і є розв’язком рівняння

де n - термін проекту.

З нерівності (70) випливає, що умова окупності інвестицій К має вигляд

Кі<E, (78)

тобто щорічні доходи повинні бути більше ніж відсоток від інвестицій.

Приклад 43.

Інвестиції на початку - 60 т. грн., доходи на протязі п’яти років 12 т. грн., 14т. грн., 17 т. грн., 19 т. грн., 21 т. грн. ( в кінці року). Знайти ВНД інвестиційного проекту.

Розв’язок.

Рівняння для і=ВНД (IRR) має вигляд:

У чарунки електронної таблиці EXCEL 5.0 послідовно вводимо: А1=-60; A2=12; A3=14; A4=17; A5=19; A6=21. Використовуємо команду ВНДОХ (А1:A6). Отримуємо результат і=11%.

Якщо інвестиції залучались за відсоток менший ніж 11%, то матимемо прибуток. Якщо відсоток залучення більший 11%, то інвестиції не окуповуються.

Приклад 44.

Пропонується продаж облігації за номіналом N=100 грн., з оголошеною доходністю 25% річних, терміном 3 роки. В кінці терміну облігація викуповується за номіналом. Продавець бере комісійні 1%. Якою буде доходність для покупця купівлі облігації?

Розв’язок.

Якщо продаж відбувається за номіналом без комісійних, то доходність дорівнюватиме оголошеній доходності 25%.

Якщо врахувати комісійні, то ставка доходності і є розв’язком рівняння:

( * * * )

Дійсно. Зліва стоїть вартість покупки облігації з комісійними. Справа - зведена величина відсотків і викупної ціни.

Рівняння ( * * * ) набуває вигляду:

або

( * * * * )

Розв’яжемо його наближеним методом (74). Оскільки ліва частина (* * * *) при і=0,25 менша за нуль, а при і=0,24 більша за нуль, то доходність лежить в межах 0,24<і<0,25. За (74) знаходимо для

та початкового наближення і₀=0,24

Отже доходність зменшилась на 0,5% у порівнянні з оголошеною по облігації.