7.3 Интегральная теорема Лапласа

Вновь предположим, что производится n испытаний, в каждом из которых вероятность появления события А постоянна и равна р (0 < р < 1). Как вычис­лить вероятность того, что событие А появится в n испытаниях не менее и не более раз (для краткости будем говорить «от до раз»)? На этот вопрос отвечает интегральная теорема Лапласа, которую мы приводим ниже.

Теорема. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что событие А появится в n испытаниях от до раз, приближенно равна определенному интегралу ,

где и .

При решении задач, требующих применения интегральной теоремы Лапласа, пользуются специальными таблицами, так как неопределенный интеграл не выражается через элементарные функции. Таблица для интеграла приведена в приложении (см. приложение 2). В таблице даны значения функции Ф(х) для положительных значений х и для х=0; для х<0 пользуются той же таблицей (функция Ф(х) нечетна, т. е. Ф(-х)=-Ф(х)). В таблице приведены значения интеграла лишь до х = 5, так как для х>5 можно принять Ф(х)=0,5. Функцию Ф(х) часто называют функцией Лапласа.

Итак, вероятность того, что событие А появится в n независимых испытаниях от до раз, ,

где и .

Пример. Вероятность того, что деталь не прошла проверку ОТК, равна р=0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей.

Решение: По условию, р=0,2; q=0,8; n=400; =70; =100. Воспользуемся интегральной теоремой Лапласа: .

Вычислим нижний и верхний пределы интегрирования.

; .

Таким образом, имеем

.

По таблице приложения 2 находим: Ф(2,5)=0,4938; Ф(1,25)=0,3944.

Искомая вероятность .

8 Понятие дсв. Распределение дсв. Функции от дсв

8.1 Случайная величина

Одним из важнейших понятий теории вероятностей является понятие случайной величины. Случайная величина является количественной характеристикой случайного результата опыта.

Случайной называют величину, которая в результате испытания принимает одно и только одно возможное значение наперёд не известное и зависящее от случайных причин, которые заранее не могут быть учтены.

Примеры:

1. количество бракованных изделий в данной партии;

2. число произведённых выстрелов до первого попадания;

3. дальность полёта артиллерийского снаряда;

4. расход электроэнергии на предприятии за месяц.

Обозначать случайные величины будем прописными буквами X, Y, Z, а их возможные значения – соответствующими строчными буквами x, y, z. Например, если случайная величина X имеет три возможных значения, то они будут обозначены так: , , .

8.2 Дискретная случайная величина (дсв)

Дискретной (прерывной) называют случайную величину, которая принимает отдельные изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Например, количество выстрелов до первого попадания в цель является дискретной случайной величиной, т.к. эта величина может принимать и бесконечное, хотя и счетное количество значений.

Законом распределения дискретной случайной величины называется соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (с помощью формулы) и графически.

Рядом распределения дискретной случайной величины называют таблицу в верхней строке которой в порядке возрастаний перечислены все значения случайной величины, а в нижней указаны соответствие вероятности.

Х	x1	x2	…	xn
p	p1	p2	…	pn

Т.к. в одном испытании случайная величина принимает только одно возможное значение то события Х= x₁, Х= x₂, …, Х= x_n образуют полную группу. По теореме о полной группе сумма вероятностей равна единице, т.е. p₁+ p₂+…+ p_n=1.

Пример 1. Брошена игральная кость. Составить закон распределения дискретной случайной величины Х-числа выпавших очков.

x	1	2	3	4	5	6
p	1/6	1/6	1/6	1/6	1/6	1/6

Закон распределения можно изобразить графически. Для этого в системе координат строят точки , ,…, и соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.

Пример 2. Вероятности того, что студент сдаст семестровый экзамен, в сессию по дисциплинам A и B, равны соответственно 0,7 и 0,9. Составить закон распределения числа семестровых экзаменов, которые сдаст студент.

Решение: Возможные значения случайной величины Х – числа сданных экзаменов – 0, 1, 2.

Пусть - событие, состоящее в том, что студент сдаст первый экзамен; - событие, состоящее в том, что студент сдаст второй экзамен. Тогда вероятности того, что студент сдаст в сессию 0, 1, 2 экзамена, будут соответственно равны:

;

Составляем ряд распределения случайной величины:

Х	0	1	2
р	0,03	0.34	0.63

И зобразим многоугольник распределения для полученного ряда (см. рис.4)

Рис. 4

При построении многоугольника распределения надо помнить, что соединение полученных точек носит условный характер. В промежутках между значениями случайной величины вероятность не принимает никакого значения. Точки соединены только для наглядности.

Пример 3. Из пяти гвоздик две белые. Составить закон распределения числа белых гвоздик среди двух одновременно взятых.

Решение: Количество белых гвоздик среди двух одновременно взятых может быть 0 или 1 или 2. Поэтому случайная величина будет принимать значения 0, 1, 2. Вероятности этих значений рассчитаем по формуле классического определения.

Закон распределения имеет вид:

X	0	1	2
р	0.3	0.6	0.1

Пример 4. В партии из 6 деталей 2 бракованные. Составить закон распределения для числа не бракованных деталей среди 3 отобранных.

Решение: Возможные значения случайной величины таковы: 1, 2, 3. Значение ноль случайная величина принимать не может, потому что ноль не бракованных деталей среди трёх отобранных означает, что все три детали будут бракованными. Но по условию задачи имеется всего две бракованные детали. Вероятности этих значений рассчитаем по формуле классического определения.

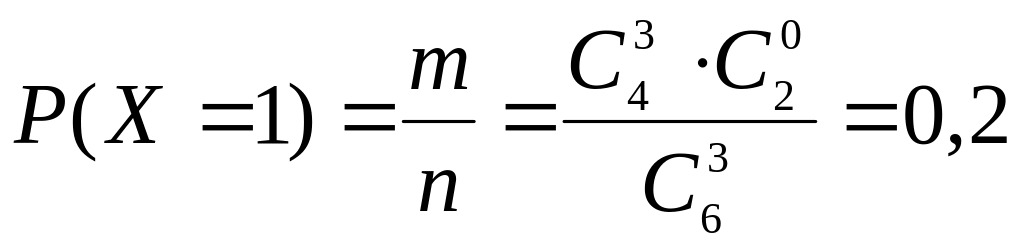
Закон распределения имеет вид:

X	1	2	3
р	0,2	0.6	0.2