4.1Расчет среднеповерхностной температуры корпуса.

1.Расчет ведется методом последовательных приближений.

м²

2.Характерный размер:

0,129м =129 мм.

3.Произвольный перегрев в первом приближении:

∆t׳ = 10˚C.

4.Температура на поверхности корпуса:

t_к׳ = t_с + ∆t׳ = 55 + 10 = 65˚C.

5.Средняя температура окружающей среды:

t_ср׳ = 0,5∙( t_с + t_к׳) = 0,5∙(55 + 65) = 60˚C.

6. Значения теплофизических параметров носителя по таблице [1]

коэффициент теплопроводности: λ = 2,9∙10 ^-2 [ ];

коэффициент кинематической вязкости: ν = 18,97∙10 ^-6 [ ];

коэффициент объемного расширения:

β = = = 3∙10 ^-3 [ ˚C ^-1 ]

7. Критерий Грасгофа :

G_r׳ = β∙g ∙ ∙( t_к׳ – t_с ) = 3∙10 ^-3 ∙ 9,8 ∙ ∙ (65 – 55) = 175,38 ∙10⁴.

где g = 9,8 [ ] – ускорение свободного падения.

8.Произведение Грасгофа на Прандтля:

P_r = 0,7 – критерий Прандтля.

(G_r׳∙P_r) = 175,38 ∙10⁴ ∙ 0,7 = 122,766 ∙10⁴.

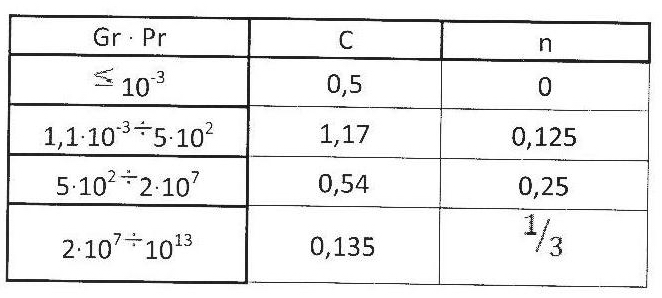
9. Значения коэффициентов, характеризующих движение теплоносителя из таблицы 4.2:

Коэффициент, отвечающий за форму тела: C = 0,54.

Коэффициент, отвечающий за тип обтекания: n = 0,25.

Таблица 4.2.

10. Критерий Нуссельта:

N_u = C∙(G_r∙P_r)ⁿ = 0,54∙(122,766 ∙10⁴)^0,25 = 17.9

11. Конвективный коэффициент теплопередачи при естественной вентиляции в неограниченном пространстве в первом приближении:

α_к׳ = N_u∙ = 17,9∙ = 4,024 [ ].

12. Лучевой коэффициент теплопередачи в первом приближении по номограмме [2]

α_лн׳ = 6,8 [ ]

Так как номограмма построена для степени черноты равной 0,8, необходима корректировка результата:

13. α_л׳ = α_лн׳ ∙ ,

где ε_пр – приведенная степень черноты в неограниченном пространстве:

14. ε_пр = = = 0,92

ε₁ = 0,92 – для красок различных цветов;

ε₂ = 1– для воздуха.

Отсюда лучевой коэффициент теплопередачи в первом приближении:

15.α_л׳ = 6,8∙ = 7,82 [ ].

16. Тепловая проводимость корпуса

конвективная проводимость корпуса:

σ_кк׳ = S_кор ∙ α_к׳ = 0,1005 ∙4,024 = 0,404[ ];

17.Лучевая проводимость корпуса:

σ_кл׳ = S_кор ∙ α_л׳ = 0,1005∙ 7,82 = 0,785 [ ];

18.Суммарная тепловая проводимость корпуса:

σ_кс׳ = σ_кк׳ + σ_кл׳ = 0,404 + 0,785 = 1,187 [ ].

19.Расчетное значение перегрева в первом приближении:

∆t_рсч׳ = = = 0,003˚C.

20.Проверка условия выполнения расчета:

| ∆t_рсч׳ – ∆t׳ | = | 0,003 – 10 | = 9,997≤ 1-2˚C => условие не выполнено, расчет продолжается.

Значение перегрева во втором приближении: ∆t׳׳ = ∆t_рсч׳ = 0,003˚C.

21.Температура корпуса:

t_к׳׳ = ∆t׳׳ + t_с = 0,003 + 55 = 55,003˚C.

22.Средняя температура окружающей среды:

1. t_ср׳׳ = 0,5∙(t_с + t_к׳׳) = 0,5∙(55 + 55,003) = 55,0015˚C.

Значения теплофизических параметров [1]:

λ = 2,865∙10 ^-2 [ ]; ν = 18,475∙10 ^-6 [ ];

β = = = 3,048∙10 ^-3 [ ˚C ^-1 ].

2 .Критерий Грасгофа во втором приближении:

G_r׳׳ = β∙g ∙ ∙ ( t_к׳׳ – t_с ) = 3,048∙10 ^-3 ∙ 9,8 ∙ ∙ ( 55,003 – 55 ) = 0,56∙10⁴

3.Произведение Грасгофа на Прандтля:

(G_r׳׳ ∙ P_r) = 0,56∙10⁴ ∙ 0,7 = 3,92∙ 10³

4.Значения коэффициентов, характеризующих движение теплоносителя по таблице 4.2:

C = 0,54; n = 0,25.

5.Критерий Нуссельта:

N_u = C∙(G_r׳׳ ∙ P_r)ⁿ = 0,54∙(3,92∙10³)^0,25 = 4,27.

6. Конвективный коэффициент теплопередачи при естественной вентиляции в неограниченном пространстве во втором приближении:

α_к׳׳ = N_u ∙ = 4,27 ∙ = 0,948 [ ].

7.Лучевой коэффициент теплопередачи по номограмме [2]

α_лн׳׳ = 6,5 [ ].

8.Лучевой коэффициент теплопередачи во втором приближении:

α_л׳׳ = α_лн׳׳ ∙ = 6,5 ∙ = 7,475 [ ].

9. Тепловая проводимость корпуса:

σ_кк׳׳ = S_кор ∙ α_к׳׳ = 0,1005 ∙ 0,948 = 0,0952 [ ];

10. σ_кл׳׳ = S_кор ∙ α_л׳׳ = 0,1005 ∙ 7,475 = 0,751 [ ];

11. σ_кс׳׳ = σ_кк׳׳ + σ_кл׳׳ = 0,0952 + 0,751 = 0,846 [ ].

12. Расчетное значение перегрева во втором приближении:

∆t_рсч׳׳ = = = 0,053˚C.

13.Проверка условия выполнения расчета:

| ∆t_рсч׳׳ – ∆t׳׳ | = | 0,053 – 0,003 | = 0,05 ≤ 1-2˚C => условие выполнено, расчет закончен.

14.Среднеповерхностная температура корпуса:

t_к = t_с + ∆t_рсч׳׳ = 55 + 0,053 = 55,053˚C.