4.2. Метод Айлиффа

М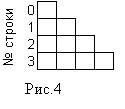 етод Айлиффа доступа к элементам массива пригоден для работы, как с прямоугольными, так и непря­мо­угольными массивами. В некоторых случаях он может оказаться более быстродействующим, так как не использует операций умножения, однако метод требует дополнительной памяти. В качестве примера рассмотрим представление двумерного массива, в котором длина i-й строки равна i+1, как это представлено на рис 4. Выделение памяти для такого массива выглядит следующим образом:

// выделим память для массива из 4-х указателей на строки

double **a=new double *[4];

// выделим память для каждой строки

for(int i=0; i<4; i++){

a[i]=new double[i+1];

}

Теперь имеем право обращаться к элементам массива как обычно: a[i][j]

Заметим, что запись a[i][j] эквивалентна записи *(*(a+i)+j), что в действительности и происходит при обращении к элементу массива a[i][j]:

• в переменной а находится адрес начала массива указателей на строки.

• прибавив к нему i, получим адрес a+i указателя на i-ю строку

• извлечем из него адрес начала i-й строки: *(a+i)

• прибавим к нему j и получим адрес j-го элемента i-й строки: *(a+i)+j

• и, наконец, извлекаем по этому адресу значение элемента массива: *(*(a+i)+j)

Как видно, операция умножения действительно не используется. Поскольку память для массива была взята из кучи, то впоследствии ее необходимо освободить. Освобождение выполняется в порядке обратном выделению:

for(int i=0; i<4; i++){

delete [] a[i];

}

delete a;

Контрольные вопросы

1. Каким образом вычисляется адрес элемента многомерного массива по его индексам?

2. Вычислите адрес элемента массива A[4][3][2], если его описание имеет вид int A[2:5][1:7][0:3]; (здесь предполагается, что нижние границы изменения индекса могут быть заданы).

3. Напишите текст фрагмента программы, создающей непрямоугольный массив из 10 строк, в котором четные строки имеют по 5 элементов, а нечетные по 8 элементов.

5. Списочные структуры

При выборе структуры хранения для некоторых данных, необ­ходимо помнить, что помимо самих данных требуется хранить струк­тур­ные связи каждого элемента данных с другими элементами. Так, например, для строки символов существенными являются не только сами символы, но и порядок их следования. Таким образом, элемент данных (символ) структурно связан с предыдущим и последующим элементом. Элемент числовой матрицы имеет соседей слева, справа, сверху и снизу. При последовательном распре­делении памяти структурные связи отображаются на физическое распо­ложение элементов структуры данных в памяти. Так, для строки следующий символ располагается вслед за текущим.

В случае связанного распределения памяти, адреса элементов, структурно связанных с элементом данных, хранятся вместе с этим элементом.

5.1. Односвязный линейный список

5.1.1. Представление односвязного списка

В качестве примера рассмотрим представления символьной строки в виде линейного списка. Каждый элемент данных хранит один символ и указатель на следующий элемент списка:

struct NODE{

char Letter; // символ

NODE *Next; // указатель на следующий элемент

};

Слово "КОРА" будет представлено списком, изображенном на рис 5.

Р ис 5. Представление строки линейным списком