2.1.2. Реализация рекурсии

Некоторые языки программирования не допускают исполь­зо­вания рекурсивных функций, то есть таких функций, которые обращаются сами к себе прямо или косвенно через другие функции. Используя стек, который функция должна обслуживать сама, программист, тем не менее, может реализовать рекурсивные алгорит­мы. Типичными задачами, решаемыми с помощью рекурсии, являются задачи перебора с возвратами (Back Track), а также алгоритмы, в которых часть работы выполняется как вся работа. В качестве примеров рассмотрим две задачи: обход шахматной доски ходом коня и вычисление определенного интеграла.

2.1.2.1. Обход шахматной доски ходом коня

К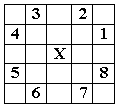 онь должен побывать в каждой клетке доски размером ровно один раз. Примем нумерацию возможных ходов коня из клетки как это изображено на рисунке. В стеке будем хранить координаты покидаемой клетки и номер выполняемого хода. Когда обнару­жит­ся, что никакой ход из клетки невозможен, берем координаты предыдущей клетки из стека и пытаемся покинуть ее с помощью хода, имеющего номер на единицу больше, чем тот ход, с помощью которого ее покидали ранее (операция "возврат"). Если уже посетили все клеток, то задача решена, и трасса обхода лежит в стеке. Если при попытке взять клетку из стека, обнаруживается, что стек пуст, то это означает, что задача не имеет решения. Ниже приведен текст программы.

struct STACK{

Int I,j; // координаты клетки

Int move; // номер хода, которым покидаем клетку

}; // элемент стека

bool Horse(int n, STACK *stack);

//-----------------------------------

static bool Move(int N, int i1,int j1, int n, int *i2, int *j2){

// Ход коня. Конь ходит из клетки i1,j1 ходом номер n

// и попадает в клетку *i2,*j2

// N - размер доски

// Возвращает true при успехе

switch(n){

case 0:

*i2=i1+1;

*j2=j1+2;

break;

case 1:

*i2=i1+2;

*j2=j1+1;

break;

case 2:

*i2=i1+2;

*j2=j1-1;

break;

case 3:

*i2=i1+1;

*j2=j1-2;

break;

case 4:

*i2=i1-1;

*j2=j1-2;

break;

case 5:

*i2=i1-2;

*j2=j1-1;

break;

case 6:

*i2=i1-2;

*j2=j1+1;

break;

case 7:

*i2=i1-1;

*j2=j1+2;

break;

default:

// сюда можно попасть только при ошибке в программе

*i2=INT_MAX;

*j2=INT_MAX;

}

return (*i2>=0 && *i2<N && *j2>=0 && *j2<N);

}

//-----------------------------------

bool Horse(int n, STACK *stack){

// n - размер доски.

// результат будет получен в стеке stack.

// Каждый раз, когда покидаем клетку, ее координаты

// и номер хода помещаем в стек.

// возврат true - успех

bool **Board=NULL; // в массиве доска n*n помечаем факт посещения клетки

Int I,j; // текущие координаты клетки

Int V; // указатель стека

Int BegMove,k,i2,j2;

bool out=true,Good;

// выделим память для доски

Board=new bool * [n];

for(i=0;i<n;i++){

Board[i]=new bool[n];

}

// Board[i][j]==true означает, что клетка посещалась

// Ни одна клетка еще не посещалась

for(i=0;i<n;i++){

for(j=0;j<n;j++){

Board[i][j]=false;

}

}

v=-1; // стек пуст

i=0;j=0; // начальная клетка

BegMove=0; // Номер хода, с которого начинается перебор

M:

// ищем допустимый ход из текущей клетки

Good=false; // предикат "Ход найден"

for(k=BegMove;k<8;k++){