Void AddToTail(mains *head, mains *V){

// изъять узел v из основного списка и вставить

// в хвост списка ведущих с головой head

// удаляем из того списка, в котором он сейчас находится

v->llink->rlink=v->rlink;

v->rlink->llink=v->llink;

// помещаем слева от head

v->rlink=head;

v->llink=head->llink;

head->llink->rlink=v;

head->llink=v;

}

5.5. Стек свободного пространства

До сих пор мы не заботились о том, куда деваются освобождаемые узлы списков, перекладывая это на алгоритмы работы с "кучей". Это было возможно, потому, что наши списки располагались в оперативной памяти и в нашем распоряжении имелись операторы new и delete. Существуют ситуации, когда программа сама должна заботиться об "утилизации" осво­бож­даемых узлов списков. Такая ситуация возникнет, если отказаться от кучи как поставщика узлов или список находится на внешнем носителе. Просто бросать освободившиеся узлы было бы слишком расточительно. Мы будем помещать их в стек свободного пространства, организованный как линейный односвязный с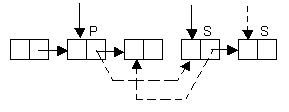 писок. Когда нам потребуется новый узел, то возьмем его из вершины стека. Операция вставки иллюстрируется рис. 20.

Рис 20. Вставка узла в список.

Текст функции приведен ниже.

NODE *InsertNode(NODE *p, NODE *s){

// Вставка узла вслед за p

// s – указатель на вершину стека свободного пространства

// возвращает указатель на новый узел

NODE *X;

X=s;

s=s->Next;

X->Next=p->Next;

p->Next=X;

return X;

}

О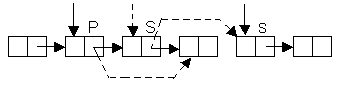 перация удаления изображена на рис 21. Удалённый узел помещается в вершину стека свободного пространства.

Рис 21. Удаление узла из списка.

Текст функции, выполняющей операцию удаления, приведен ниже.

Void DeleteNode(node *p, node *s){

// узел, следующий за p удаляется и помещается

// в вершину стека свободного пространства s

NODE *X;

X=p->Next; // X-удаляемый узел

p->Next=X->Next;

X->Next=s;

s=X;

}

Для списочных структур на внешнем носителе роль указателя играет смещение узла относительно начала файла.

5.6. Обслуживание свободного пространства

Для списков общего вида удаляемый из одного списка узел не может быть просто отправлен в стек свободного пространства, так как он может входить более чем в один список. Для обслуживания свободного пространства могут быть использованы методы счетчиков ссылок и сбор мусора.

5.6.1. Счетчик ссылок

В методе счетчиков ссылок каждый узел содержит поле счетчика int count, равное числу узлов, ссылающихся на данный. При удалении узла из списка поле count уменьшается на единицу. Когда счетчик окажется равным нулю, узел можно отправить в свободное пространство. Метод не работает для рекурсивных списков, в которых узел может прямо или косвенно ссылаться на самого себя. Такой узел никогда не будет освобожден.

5.6.2. Сбор мусора

При использовании метода "сбор мусора" программы беззаботно рабо­тают до тех пор, пока не будет исчерпано свободное простран­ство. Брошенные и никем неиспользуемые узлы называют мусором. Когда свободное пространство исчерпано, вызывается мусорщик, целью которого является собрать мусор в стек свободного простран­ства. Каждый узел имеет бит маркировки. Метод работает в три фазы. В первой фазе обходится вся память, занятая списками и биты маркировки устанавливаются в "0". Вторая фаза систематически обходит все узлы списков и устанавливает в них бит маркировки в "1". Таким образом, маркированными нулём остаются только узлы, относящиеся к мусору. Третья фаза вновь обходит всю память и собирает узлы, помеченные нулем в стек свободного пространства.

Время работы мусорщика выражается формулой

, где

C₁, C₂ – константы, N – число всех узлов в списках, M – число всех узлов в памяти, отведенной под списки.

Таким образом, M-N – количество узлов, возвращаемых мусорщиком в стек свободного пространства. Время, расходуемое на возврат одного узла, составляет

Обозначим коэффициент загрузки памяти, тогда время, требуемое на возврат одного узла, составит

К ак видно из последней формулы, недостатком метода является то, что он медленно работает, когда загрузка памяти велика. В таких случаях число узлов, возвращаемых в стек свободного простран­ства не окупает затраченных усилий. Те программы, которым не хватает памяти, впустую расходуют массу времени, многократно и бесплодно вызывая мусорщика перед тем, как окончательно исчерпать память. Метод сбора мусора малопригоден для работы в реальном времени, так как он вызывается в непредвиденные моменты времени и может долго работать.