18. Перетворення Лоренца. Простір і час в ств.

Покажемо, як з принципів Ейнштейна випливають формули перетворень Лоренца, знайдені на основі рівнянь електродинаміки та припущення Фітцджеральда.

Розглянемо дві інерціальні системи координат OXYZ та ОXYZ, які рухаються з відносною швидкістю , тобто початок координат О має швидкість в системі OXYZ. Припустимо, що в точках О та О знаходяться точкові джерела світла. Фронт світлової хвилі, який поширюється з швидкістю в системі OXYZ описується рівнянням

. (19.1)

Згідно загального принципу відносності цей фронт повинен описуватися таким же рівнянням і в системі OXYZ, початок O якої в момент часу співпадає з О:

. (19.2)

Шукане перетворення повинно задовольняти умові інваріантності

,

Звідки . (19.3)

При цьому зауважимо, що перетворення повинно бути лінійним, оскільки в протилежному випадку порушиться однорідність простору і часу: їх властивості залежали б від вибору початку відліку.

Нехай осі ОХ та ОХ обох систем співпадають, а осі ОY та ОZ паралельні, відповідно, осям ОY та ОZ і перпендикулярні напряму відносної швидкості руху систем. Тоді найбільш загальним лінійним зв’язком між координатами Y та Y і Z та Z з урахуванням ізотропності простору буде .

В силу рівноправності обох систем обернені перетворення матимуть такий же вигляд:

.

Порівнюючи останні вирази, приходимо до висновку, що , причому випадок відповідає протилежному напрямкові штрихованих осей і є несуттєвим. Таким чином, для розглянутих координат перетворення є тотожним: .

Тому рівняння (19.3) запишеться у вигляді .

Отримана рівність буде виконуватись у тому випадку, коли

Звідси знаходимо, що

, (19.4)

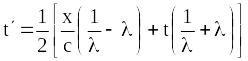, (19.5)

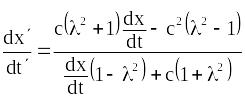. (19.6)

Проаналізуємо останній вираз. Якщо світло поширюється в системі OXYZ з швидкістю вздовж осі ОХ, то

,

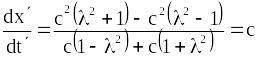значить і в системі ОXYZ швидкість поширення світла дорівнюватиме , що підтверджує еквівалентність рівності (19.3) принципу сталості швидкості світла у вакуумі.

Якщо система ОXYZ рухається відносно ОXYZ рівномірно й прямолінійно з швидкістю , то для початку О цієї системи . Тоді (19.6) набуває вигляду

, звідки 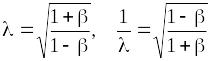, (19.7)

де . З урахуванням отриманих виразів співвідношення (19.4) і (19.5) запишуться:

.

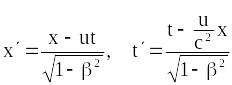Таким чином, перетворення Лоренца мають вигляд

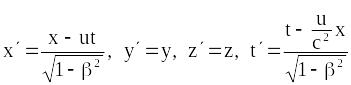. (19.8)

Формули оберненого перетворення отримують, змінюючи знак біля швидкості :

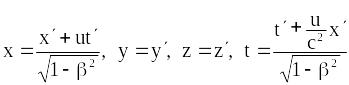. (19.9)

Легко бачити, що при формули перетворень Лоренца переходять в перетворення Галілея.

Продовження це питання 19. Кінематичні наслідки перетворень Лоренца: ефекти скорочення довжини і сповільнення часу. Відносна швидкість, перетворення швидкостей.

19. Кінематичні наслідки перетворень Лоренца: ефекти скорочення довжини і сповільнення часу. Відносна швидкість, перетворення швидкостей.

Розглянемо деякі кінематичні наслідки перетворень Лоренца.

Нехай в системі OXYZ знаходиться в стані спокою стержень, паралельний осі ОХ. Його довжина, виміряна в цій системі у фіксований момент часу, рівна , де – координати початку й кінця стержня. Довжина стержня в системі OXYZ: . Тоді на основі першої рівності (19.8) при фіксованому маємо ,

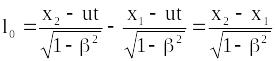звідки . (19.10)

Отже, довжина стержня в системі, що рухається відносно нього з швидкістю , скорочується пропорційно множнику . Це означає, що просторові відстані не є інваріантами перетворень Лоренца, а змінюються при переході від однієї інерціальної системи відліку до іншої. Оскільки за вказаних вище умов поперечні розміри тіла не змінюються, то об’єм тіла в рухомій відносно нього системі визначається співвідношенням

. (19.11)

Розглянемо тепер, як будуть сприйматися проміжки часу між двома подіями з точки зору різних інерціальних систем відліку. Визначимо в системі OXYZ проміжок часу між двома подіями, що відбуваються в одній і тій же точці системи OXYZ. Оскільки

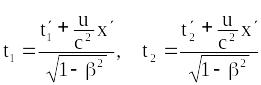, то . (19.12)

Таким чином, проміжки часу також мають відносний характер: рухомий годинник йде повільніше, ніж нерухомий. Сповільнення ходу годинника відбувається пропорційно множнику . При цьому слід зауважити, що тривалість процесу, або проміжок часу між двома подіями, найменший в тій системі, де події відбуваються в одній і тій же точці простору. Цей проміжок часу називається власним часом :

. (19.13)

Знайдемо співвідношення, які пов’язують швидкість тіла в одній системі відліку з швидкістю того ж тіла в іншій системі.

Нехай система OXYZ рухається відносно OXYZ з швидкістю вздовж осі ОХ. При цьому і є компонентами швидкості тіла в системах OXYZ та OXYZ, відповідно. З (19.8) маємо:

,

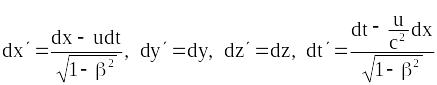Поділивши перші три рівності на четверту, знаходимо:

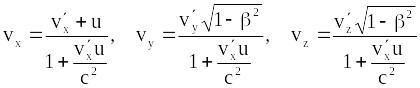. (19.14)

Ці формули і визначають перетворення швидкостей. Вони являють собою закон додавання швидкостей в спеціальній теорії відносності. В граничному випадку вони переходять в формули класичної механіки

.

Три формули (19.14) можна записати у вигляді однієї векторної рівності

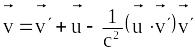. (19.15)

При цьому слід звернути увагу, що в релятивістський закон додавання швидкостей дві складові та входять несиметрично (якщо тільки обидві вони не напрямлені вздовж осі Х). Ця обставина закономірно пов’язана з некомутативністю перетворень Лоренца.¹

Виберемо осі координат так, щоб швидкість частинки в даний момент лежала в площині XY. Тоді швидкість частинки в системі OXYZ має проекції ,

а в системі OXYZ – , де і – кути, утворені швидкістю з осями Х та Х відповідно. На основі формул (19.14) знаходимо:

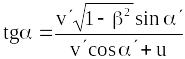. (19.15)

Співвідношення (19.15) визначає зміну напряму швидкості при переході від однієї інерціальної системи відліку до іншої.

Приклад 19.1. Частинка рухається у площині по колу радіуса згідно закону

.

В момент часу швидкість частинки . Знайти рівняння траєкторії в системі К, яка рухається з швидкістю .

На основі перетворень Лоренца (19.8) отримуємо:

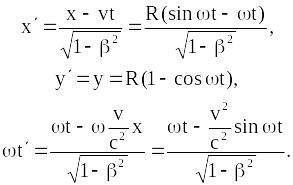
Для частинок, які рухаються з швидкістю , величина

.

Тому в інтервалі часу , який задовольняє умові , маємо

,

.

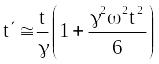Рівняння траєкторії

.
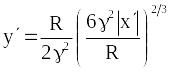