14. Два методи побудови класичної механіки. Виведення рівнянь Лагранжа з принципу екстремальної дії.

В основу механіки можуть бути покладені закони Ньютона, які є результатом широкого узагальнення дослідних фактів. Ці закони, являючись з логічної сторони аксіомами, дають можливість отримувати основні теореми і висновки механіки. Відмінною рисою такої схеми побудови класичної механіки є підхід до сили як причини зміни механічного стану.

В основі другого методу, який у фізичному плані є більш формальним, але разом з тим і більш загальним, лежить інтегральний варіаційний принцип Гамільтона–Остроградського. Вихідними поняттями тут виступають дія та функція Лагранжа. Можливість побудови класичної механіки на принципі екстремальної дії ґрунтується на тому, що його використання дає можливість отримувати рівняння руху механічних систем. Проілюструємо це на прикладі рівнянь Лагранжа і Гамільтона.

Нехай дійсний рух системи описується функціями . Функціонал для такого руху

.

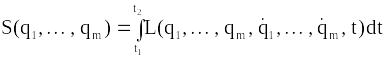Проваріюємо цей інтеграл:

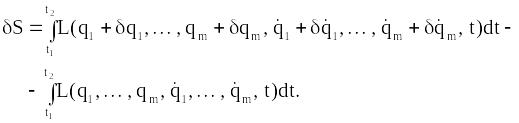
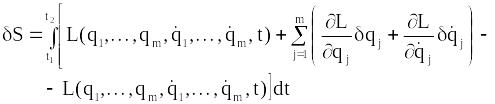
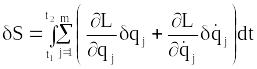. (13.18)

Оскільки 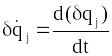, то вираз (13.18) можна записати у вигляді

.

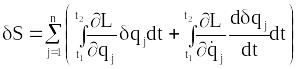Другий інтеграл беремо частинами:

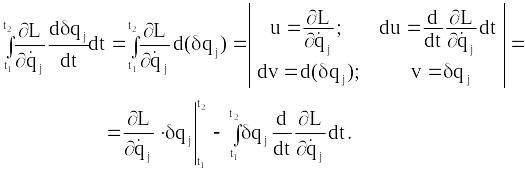
В силу умови (13.7,б) перша складова перетворюється в нуль. У результаті отримуємо

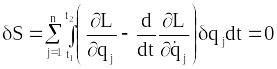. (13.19)

Рівність (13.19) повинна виконуватись при довільних відмінних від нуля значеннях , і тому має місце необхідна й достатня умова екстремуму дії у вигляді рівнянь, що виконуються для підінтегральних виразів: .

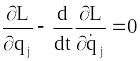Ми прийшли до рівнянь Лагранжа другого роду для систем, що рухаються у потенціальних силових полях.

Отримаємо тепер канонічні рівняння з рівності (13.13), провівши операцію варіювання:

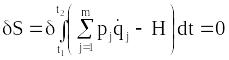. (13.20)

Варіюючи підінтегральний вираз, маємо

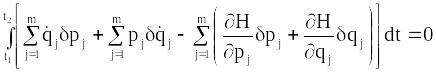. (13.21)

Інтегруючи за частинами, знайдемо .

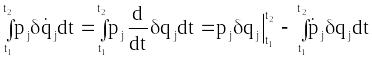На основі умов (13.7,б) отримаємо .

Тоді інтеграл (13.21) запишеться у вигляді .

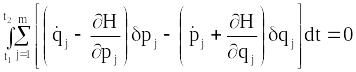Як і раніше приходимо до висновку, що підінтегральний вираз рівний нулю:

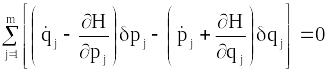. (13.22)

Вираз (13.22) може бути рівним нулю при довільних незалежних і лише за умови

,

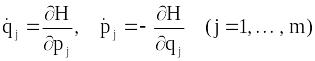тобто отримуємо систему канонічних рівнянь Гамільтона.

Принцип екстремальної дії охоплює не тільки механічні явища, знаходячи своє використання в інших розділах теоретичної фізики. Таке широке застосування принципу тісно пов’язане з методом узагальнених координат. Рівняння Лагранжа не обмежені евклідовим простором. Тільки для вільної точки вони є рівняннями руху в координатах тривимірного простору. У випадку системи з зв’язками автоматичне урахування дії сил реакцій зв’язків здійснюється вже самим вибором узагальнених координат, а їх число визначає вимірність простору конфігурацій. Перехід до нескінченно вимірного простору дозволяє застосувати принцип екстремальної дії до систем з нескінченним числом ступенів вільності – фізичних полів.

15. Виведення канонічного рівняння Гамільтона з принципу екстремальної дії.

Рівняння Лагранжа, як і рівняння Гамільтона, мають однакову форму незалежно від конкретного змісту узагальнених координат. Це означає, що при переході до нових координат вказані рівняння зберігають свій вигляд, хоча геометричний зміст координат та імпульсів (а також вигляд функцій і ) буде іншим.

Іноді доцільно користуватись перетворенням типу

, (13.23)

коли нові координати залежать не тільки від старих координат, але й від імпульсів. При цьому рівняння руху, взагалі кажучи, втрачають вигляд рівнянь Гамільтона. Однак можна знайти такий клас перетворень, при яких вид рівнянь Гамільтона зберігатиметься. Такі перетворення називаються канонічними.

До формул для канонічних перетворень можна прийти наступним шляхом. Як було показано вище, рівняння Гамільтона можуть бути отримані з принципу екстремальної дії. Для того, щоб нові змінні також задовольняли рівнянням Гамільтона, для них також повинен справджуватись принцип екстремальної дії 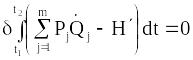, (13.24)

де – функція Гамільтона в нових канонічних змінних. Таким чином, шукане перетворення (13.23) повинно переводити варіаційну рівність (13.20) в рівність (13.24) і навпаки. Це можливо лише за умови, що їх підінтегральні вирази відрізняються тільки на повний диференціал довільної функції часу, старих і нових узагальнених координат:

. (13.25)

Отже, 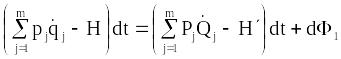. (13.26)

Будь-яке канонічне перетворення характеризується своєю функцією , яку називають твірною функцією перетворення.

Виходячи з рівності (13.25), знайдемо .

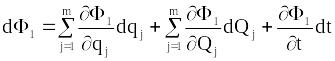Підставляючи цей вираз у (13.26), отримаємо

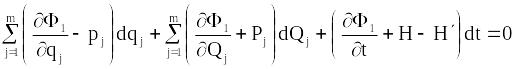. (13.27)

Розглядаючи час , координати і як незалежні змінні, на основі рівності (13.27) отримуємо 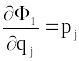, , 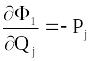(13.28)

При заданій функції формули (13.28) встановлюють зв’язок між старими і новими змінними і дають вираз для нової функції Гамільтона.

Іноді зручніше виражати твірну функцію не через змінні і , а через старі координати і нові імпульси . Для виведення формул канонічних перетворень у цьому випадку потрібно провести у співвідношенні (13.26) відповідне перетворення Лежандра:

.

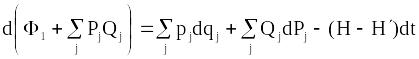Вираз, який стоїть під знаком диференціалу в лівій частині останньої рівності, виражений через змінні і , і є новою твірною функцією :

. (13.29)

Провівши відносно цієї функції операції, аналогічні попереднім, отримаємо

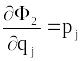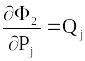, , . (13.30)

Аналогічно можна перейти до формул канонічних перетворень, виражених через твірні функції, що залежать від змінних і .

Зв’язок між новою та старою функціями Гамільтона завжди виражається однаково: їх різниця визначається частинною похідною по часу від твірної функції. Зокрема, якщо остання не залежить від часу, то . Іншими словами, у цьому випадку для отримання нової функції Гамільтона достатньо підставити в величини , , виражені через нові змінні , .