11. Дужки Пуассона, їх властивості.

Нехай і – двічі неперервно диференційовані функції узагальнених координат, імпульсів і часу. Вираз

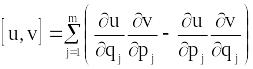(12.19)

називають дужками Пуассона функцій і .

Відмітимо основні властивості дужок Пуассона.

1. Антикомутативність:

. (20.20)

2. Якщо одна з функцій стала (наприклад, ), то . (20.21)

3. . (20.22)

4. . (20.23)

5. . (20.24)

Ці властивості безпосередньо випливають з означення (12.19) дужок Пуассона.

Якщо одна з функцій або співпадає з одним з імпульсів або координатою, то дужки Пуассона зводяться до частинної похідної:

, (12.25)

. (12.26)

Дійсно, якщо, наприклад, , то

.

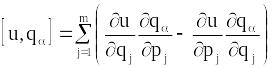При цьому , а ( , якщо і , якщо ). В результаті приходимо до виразу (12.25). Аналогічно доводиться і співвідношення (12.26).

Дужки Пуассона, взяті для самих канонічних змінних (тобто ) називаються фундаментальними дужками Пуассона:

(12.27)

Для дужок Пуассона, складених з трьох функцій, справедлива тотожність Якобі:

. (12.28)

Розглянемо деяку функцію координат, імпульсів і часу . Її повна похідна по часу рівна 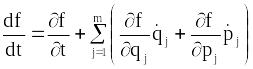, або, використавши рівняння Гамільтона,

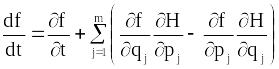. (12.29)

Згідно визначення (12.19), друга складова у правій частині формули (12.29) є дужками Пуассона для функцій і . З урахуванням цього співвідношення (12.29) запишеться у вигляді

. (12.30)

Якщо функція є інтегралом руху, то її повна похідна по часу рівна нулю. У цьому випадку . (12.31)

Вираз (12.31) є необхідною і достатньою умовою того, що функція – перший інтеграл.

Має місце наступне твердження, відоме як теорема Пуассона-Якобі:

якщо функції і є інтегралами руху, то складені з них дужки Пуассона також є інтегралами руху.

Доведення.

Запишемо повну похідну функції по часу:

.

Використовуючи співвідношення (12.24) і (12.28), останній вираз перепишемо у вигляді

,

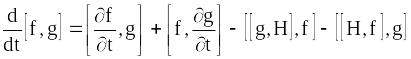або, врахувавши формули (12.20) і (12.22),

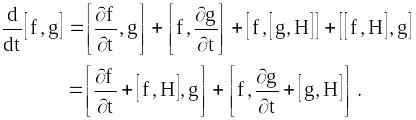
Оскільки функції і є інтегралами руху, то, згідно (12.31)

, .

В результаті отримаємо

,

тобто функція – інтеграл руху.

Ця теорема дає можливість в деяких випадках отримувати нові інтеграли руху.

Повна похідна по часу довільної функції канонічних змінних, яка не залежить від часу явно, згідно (12.30) визначається рівністю 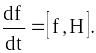(12.32)

Характерно, що значення в момент часу виражається через значення в момент часу наступною формулою:

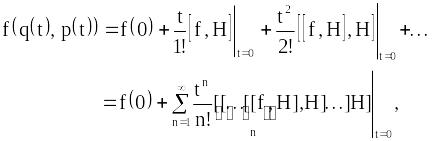(12.33)

де , задовольняють канонічним рівнянням, що описують еволюцію механічної системи, гамільтоніан якої явно від часу не залежить; . Ряд у правій частині (12.33) за припущенням збіжний.

Як приклад розглянемо просту задачу, яка допускає точний розв’язок. Знайдемо , в задачі гармонічного осцилятора. Гамільтоніан системи

Покладемо і обчислимо дужки Пуассона:

Тоді права частина формули (12.33) для функції :

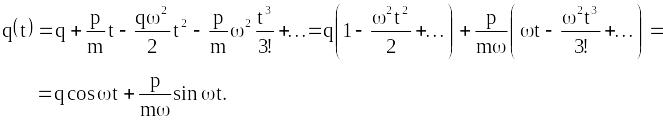
Функції і ми встановили за першими двома членами їх розкладу.

Аналогічно, покладаючи і обчислюючи дужки Пуассона

для отримаємо

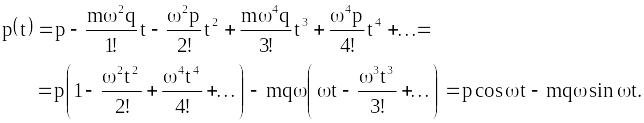
Отримані формули для і визначають стан системи в момент часу , тобто є розв’язками канонічних рівнянь для гармонічного осцилятора.