Доверительный интервал для математического ожидания нормального распределения при неизвестной дисперсии
Пусть количественный признак X генеральной совокупности распределен нормально, причем среднее квадратическое отклонение этого распределения неизвестно. Требуется оценить неизвестное математическое ожидание с помощью доверительных интервалов.
Оказывается,
что по данным выборки можно построить
случайную величину
,
которая имеет распределение Стьюдента
с
степенями свободы. В последнем выражении
–
– выборочное
среднее,
– исправленное среднее квадратическое
отклонение,
– объем выборки; возможные значения
случайной величины T
мы будем обозначать через t.
Плотность распределения Стьюдента
имеет вид:
,
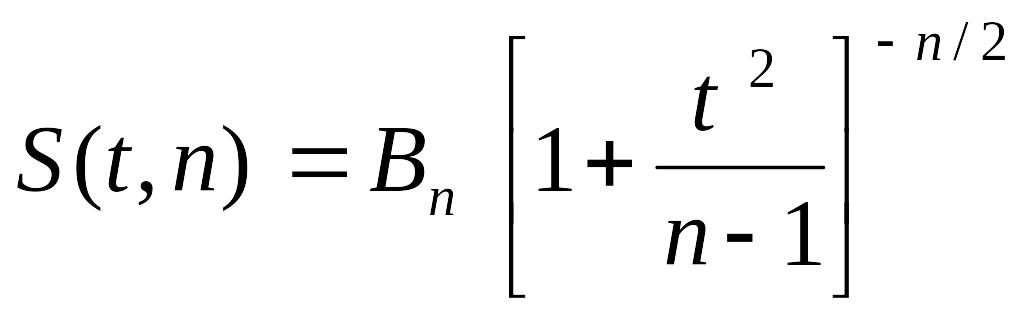где
некоторая постоянная, выражающаяся
через гамма–функции. Как видно,
распределение Стьюдента определяется
параметром n
– объемом выборки (или, что то же самое
– числом степеней свободы
)
и не зависит от неизвестных параметров
.
Поскольку
– четная функция от t
, то вероятность выполнения неравенства
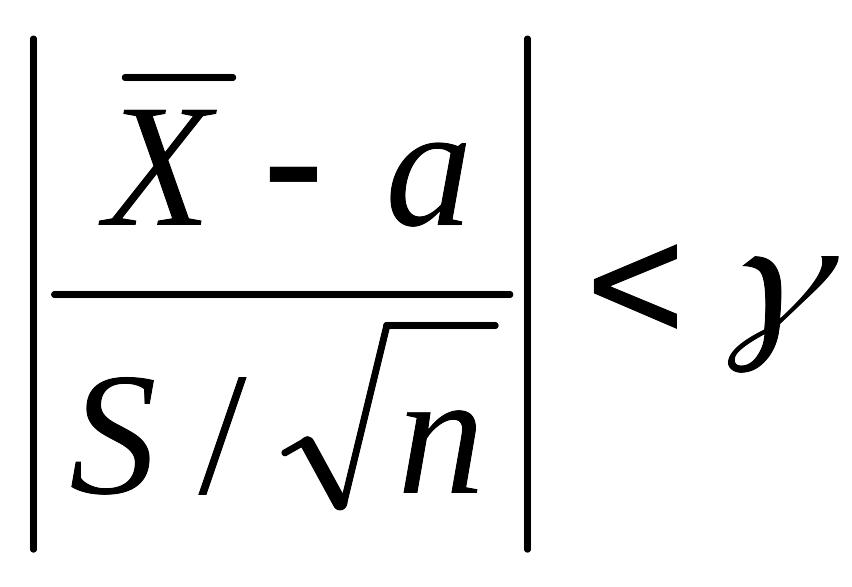определяется следующим образом:
.
Заменив неравенство в круглых скобках двойным неравенством, получим выражение для искомого доверительного интервала:
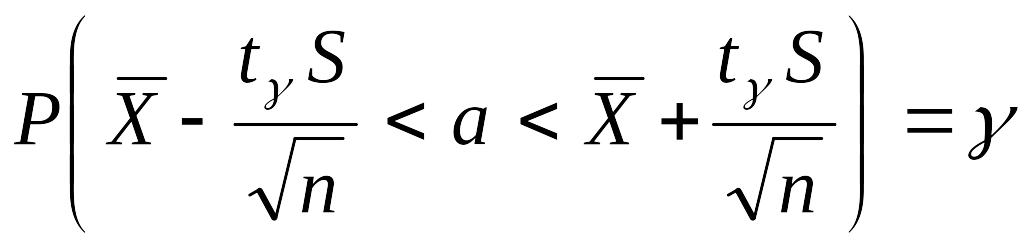
Итак,
с помощью распределения Стьюдента
найден доверительный интервал
,
покрывающий неизвестный параметр a
с надежностью
.
По таблице распределения Стьюдента и
заданным n
и
можно найти
,
и, используя найденные по выборке
и
,
можно определить доверительный интервал.
Пример.
Количественный признак X
генеральной совокупности распределен
нормально. По выборке объема n=16
найдены генеральное среднее
и исправленное среднее квадратическое
отклонение
.
Требуется оценить неизвестное
математическое ожидание при помощи
доверительного интервала с надежностью
0,95.
Решение.
Найдем
по таблице распределения Стьюдента,
используя значения
.
Этот параметр оказывается равным 2,13.
Найдем границы доверительного интервала:
.
То
есть с надежностью 0,95 неизвестный
параметр a
заключен в доверительном интервале
.
Можно показать, что при возрастании объема выборки n распределение Стьюдента стремится к нормальному. Поэтому практически при n>30 можно вместо него пользоваться нормальным распределением. При малых n это приводит к значительным ошибкам.
Доверительный интервал для оценки среднего квадратического отклонения нормального распределения
Пусть количественный признак X генеральной совокупности распределен нормально и требуется оценить неизвестное генеральное среднее квадратическое отклонение по исправленному выборочному среднему квадратическому отклонению s. Найдем доверительные интервалы, покрывающие параметр с заданной надежностью .
Потребуем, чтобы выполнялось соотношение:
или
.
Преобразуем
двойное неравенство
в равносильное неравенство
и обозначим /s=q.
Имеем:
(A)
и необходимо найти
q.
С этой целью введем в рассмотрение
случайную величину
.
Оказывается,
величина
распределена по закону
с n–1
степенями свободы. Плотность распределения
имеет вид:
Это распределение не зависит от оцениваемого параметра , а зависит только от объема выборки n.
Преобразуем
неравенство (A)
так, чтобы оно приняло вид
.
Вероятность этого неравенства равна
заданной вероятности
,
т.е.
.
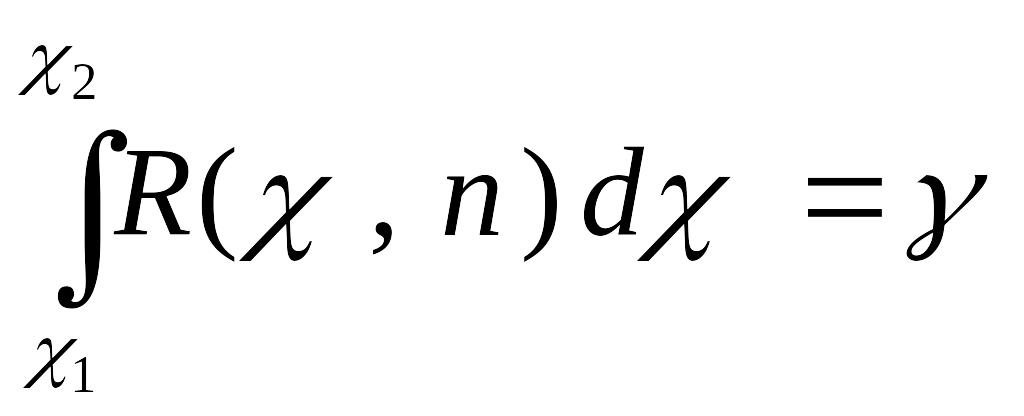Предполагая, что q<1, перепишем (A) в виде:
,
далее,
умножим все члены неравенства на
:
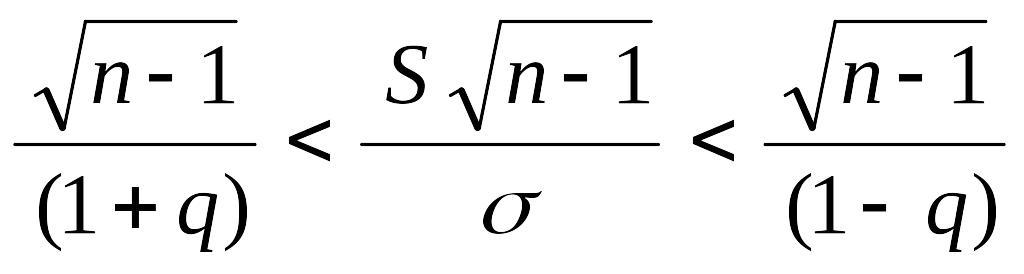или
.
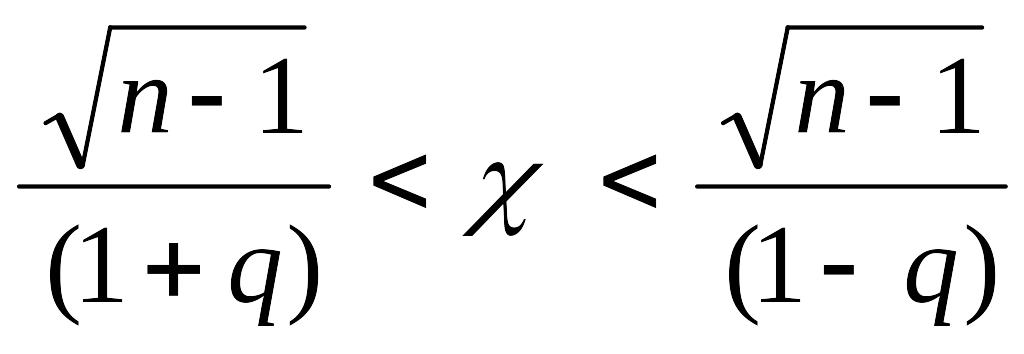Вероятность того, что это неравенство, а также равносильное ему неравенство (A) будет справедливо, равна:
.
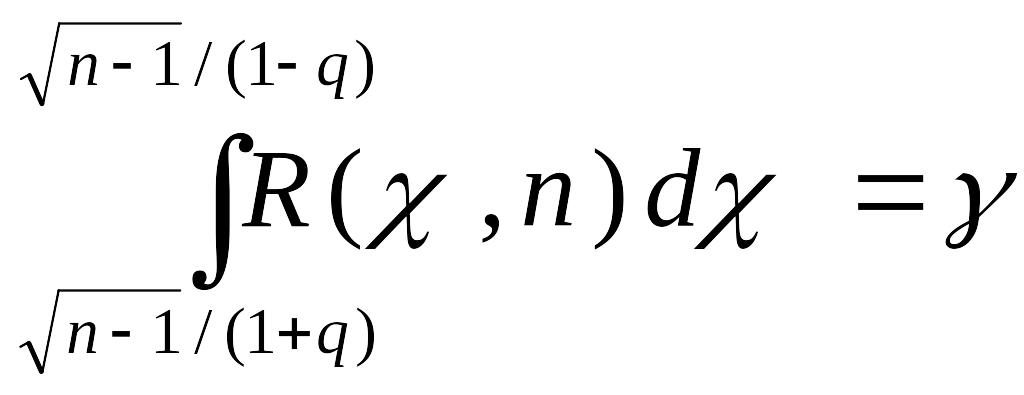Из
этого уравнения можно по заданным
найти
,
используя имеющиеся расчетные таблицы.
Вычислив по выборке
и найдя по таблице
,
получим искомый интервал (A1),
покрывающий
с заданной надежностью
.
Пример. Количественный признак X генеральной совокупности распределен нормально. По выборке объема n=25 найдено исправленное среднее квадратическое отклонение s=0.8. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение с надежностью 0,95.
Решение.
Используя заданные значения
,
по таблице находим значение q=0.32.
Искомый доверительный интервал есть:
.
Необходимо сделать замечание. Мы предполагали, что q<1. Если это не так, то мы придем к соотношениям:
.
Следовательно, значение q >1 может быть найдено из уравнения:
