19.Операции над множествами

Рассмотрим методы получения новых множеств их уже существующих.

Определение 1.4. Пересечением множеств А и В называется множество С , состоящее из всех элементов, одновременно входящих и в множество А, и во множество В. Это записывается следующим образом:

	(1.3)
Свойства операции пересечения множеств: (коммутативность); (ассоциативность); ; ; Ø = Ø.

Пример 1.7. Если множество А есть интервал (1; 5) а множество В есть интервал (2; 7), то пересечение множеств А и В есть интервал (2; 5): .

Определение 1.5. Объединением множеств А и В называется множество С, состоящее из всех элементов, каждый из которых принадлежит хотя бы одному из данных множеств или А, или В, или А и В одновременно. Это обозначается следующим образом:

	(1.4)
Свойства операции объединения множеств: (коммутативность); (ассоциативность); (дистрибутивность); ; ; Ø = Ø.

Пример 1.8. Если множество А есть отрезок [1; 3] а множество В есть отрезок [2; 5], то объединение множеств А и В есть отрезок [1; 5]: .

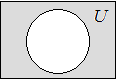
Определение 1.6. Дополнением множества А называется множество всех элементов универсального множества U, каждый из которых не принадлежит множеству А.

Дополнение множества А будем обозначать через

Свойства операции дополнения множеств: ; Ø

Пример 1.9. Если множество А есть отрезок [1; 3], то множество представляет собой объединение двух интервалов: .

Определение 1.7. Разностью множеств А и В называется множество С, состоящее из всех элементов, принадлежащих множеству А, но не принадлежащих В:

.

(1.5)

Операция вычитания множеств не коммутативна: . Из определения разности множеств следует, что имеет место равенство .

Пример 1.10. Если множество А есть отрезок , а множество В есть отрезок , то разность представляет собой полуинтервал , а полуинтервал .

Определение 1.8. Симметрической разностью множеств А и В называется множество С, состоящее из всех элементов, принадлежащих множествам А и B, но не принадлежащих их общим областям.

.

(1.6)

Другими словами симметрическая разность двух множеств и состоит из элементов, которые принадлежат ровно одному из множеств: либо только , либо только .
Операция симметрической разности для трех множеств ассоциативна:

_{Пример 1.11. Если , , то .}

Определение 1.9. Декартовым произведением двух множеств А и В называется множество С, состоящее из всевозможных пар элементов , у которых и .

(1.7)

Пример 1.12. Даны два множества: , . Для этих множеств можно составить два варианта декартового произведения этих множеств: и

Из примера видно, что множества и различны.

Пример 1.13. Пусть множество А есть отрезок ,на некоторой прямой, а множество В есть отрезок другой прямой. Тогда декартово произведение , включающее многочисленные пары координат, составит прямоугольник на плоскости.

.