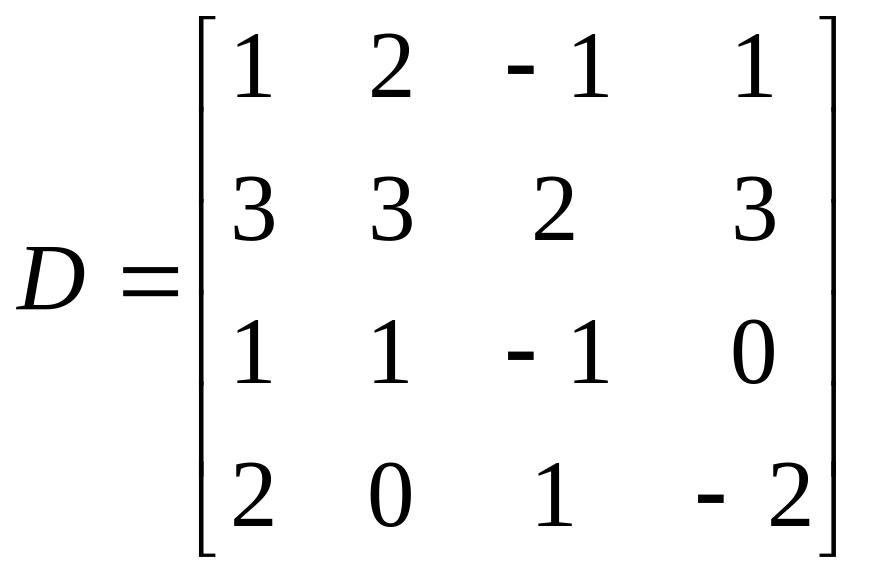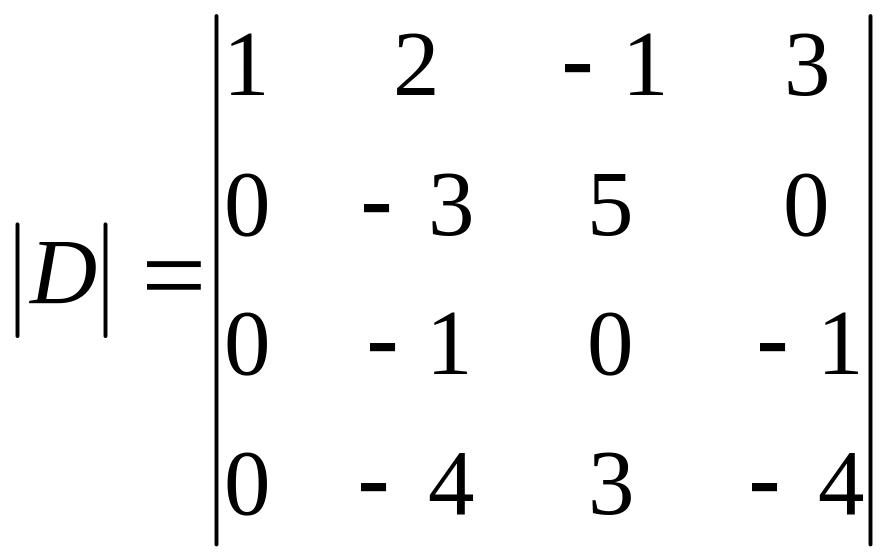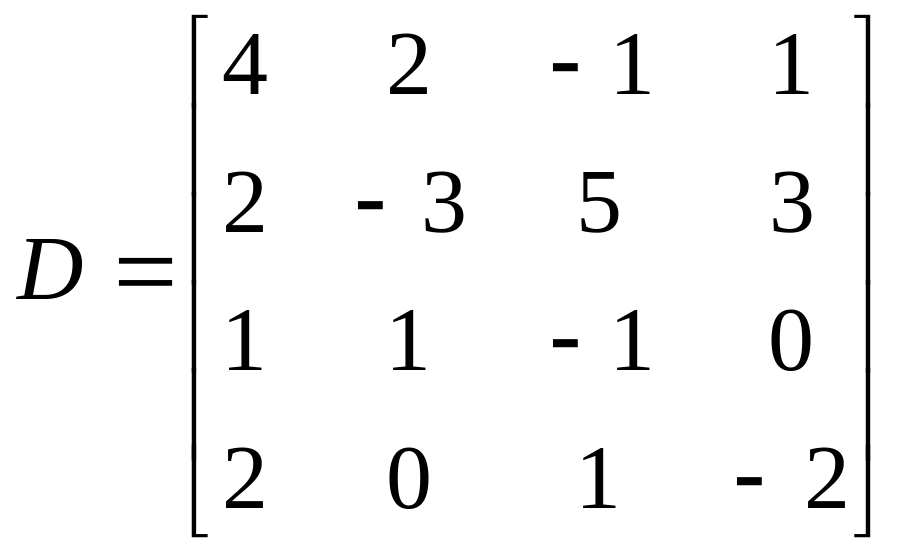9.Свойства определителей

Сформулируем основные свойства определителя:

1. При транспонировании матрицы определитель не меняется:

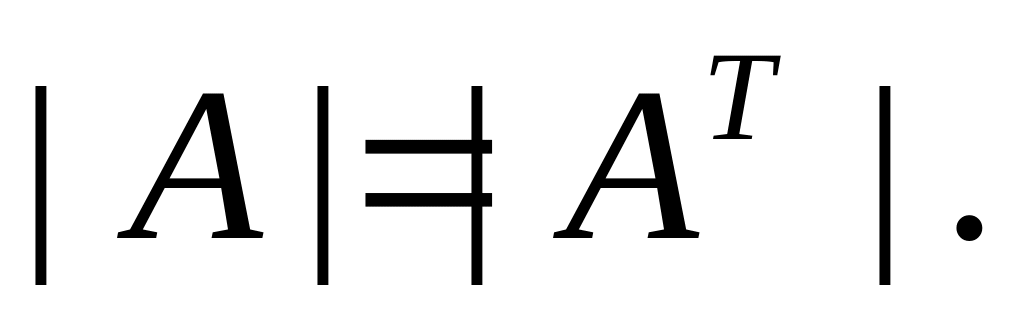
2. Если матрица А имеет нулевую строку или нулевой столбец, то и определитель равен нулю: .

3. Если переставить местами две любые строки или два любых столбца, то определитель поменяет знак.

4. Если А имеет две одинаковые строки или два одинаковых столбца, то .

5. Если все элементы какой-либо строки или столбца матрицы умножить на число, то определитель умножится на это число.

6. Если определитель имеет две пропорциональные строки или два пропорциональных столбца, то он равен нулю.

7. Определитель не изменится, если к какой-либо строке (столбцу) прибавить другую строку (столбец), умноженную на число.

8. Определитель произведения двух квадратных матриц равен произведению определителей этих матриц:

(2.16)

10. Обратная матрица

Понятие обратной матрицы вводится только для квадратных матриц.

Определение 3.3. Если А — квадратная матрица, то обратной для нее матрицей называется матрица, обозначаемая А^-1 и удовлетворяющая условию

(3.3)

Теорема 3.1. (об обратной матрице): Для того, чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы матрица А была невырожденной, т. е. чтобы ее определитель был отличен от нуля.

Для простоты на примере матрицы третьего порядка приведем последовательность вычислений, которая позволяет построить обратную матрицу.

Пусть

(3.4)

Невырожденная матрица, т. е. её определитель

(3.5)

Составим новую матрицу В, заменяя в матрице А каждый ее элемент а_ij его алгебраическим дополнением А_ij, деленным на определитель |A| матрицы А:

(3.6)

Построим матрицу В^Т, транспонированную по отношению к матрице В:

(3.7)

Покажем, что матрица В^Т, является обратной матрице А. Для этого составим произведение:

Так как. числители элементов на главной диагонали равны |A| (раскрытие определителя по элементам строки), а числители всех остальных элементов равны нулю (сумма произведений элементов одной строки или столбца на алгебраические дополнения другой строки или столбца равна нулю).

Таким образом, откуда Итак, способ построения обратной матрицы получен:

.

(3.8)

Пример 3.1. Дана матрица

Найти обратную матрицу.

Вычислим определитель матрицы А:

Находим алгебраические дополнения элементов этого определителя по формулам

Следовательно,

11.Элементарные преобразования матриц

При вычислении обратной матрицы, как правило, приходится вычислять большое число определителей. Чтобы облегчить этот процесс, применяют специальные приемы, которые называют элементарными преобразованиями матриц.

Элементарными называются следующие преобразования:

• умножение всех элементов какой-либо строки (столбца) матрицы на одно и то же число, отличное от нуля;

• прибавление к элементам какой-либо строки (столбца) матрицы соответствующих элементов другой строки (столбца), умноженных на одно и то же число;

• перемена местами строк (столбцов) матрицы;

• отбрасывание строк (столбцов) матрицы, все элементы которых равны нулю.

Матрицы, получающиеся одна из другой при элементарных преобразованиях, называются эквивалентными.

Пример 4.1. Вычислить определитель матрицы:

(4.1)

Преобразуем матрицу так, чтобы не вычислять много миноров. Для этого в первом столбце во второй, третьей и четвертой строках получим нули. Работу начнем со второй строки, первую строку перепишем без изменений. Воспользуемся элементарными преобразованиями матрицы и ко второй строке прибавим первую, умноженную на :

(4.2)

Теперь к третьей строке прибавим первую строку, умноженную на :

(4.3)

И, наконец, к четвертой строке прибавим первую, умноженную на :

(4.4)

Определитель полученной матрицы равен произведению элемента на его алгебраическое дополнение:

Пример 4.2. Вычислить определитель матрицы:

(4.5)

Преобразуем матрицу так, чтобы под главной диагональю стояли нули. ПоДля этого в первом столбце во второй, третьей и четвертой строках получим нули. Работу начнем со второй строки, первую строку перепишем без изменений. Воспользуемся элементарными преобразованиями матрицы и ко второй строке прибавим первую, умноженную на :

(4.6)

Теперь к третьей строке прибавим первую строку, умноженную на :

(4.7)

И, наконец, к четвертой строке прибавим первую, умноженную на :
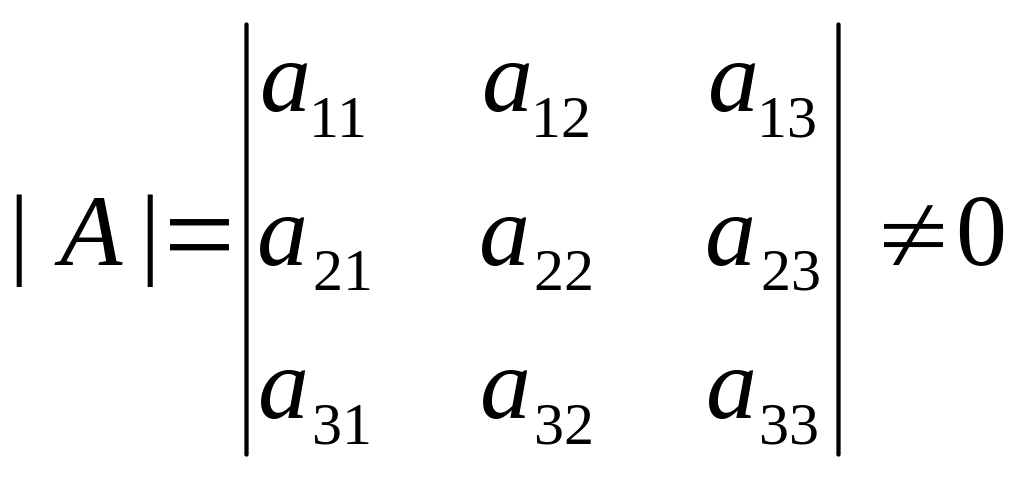
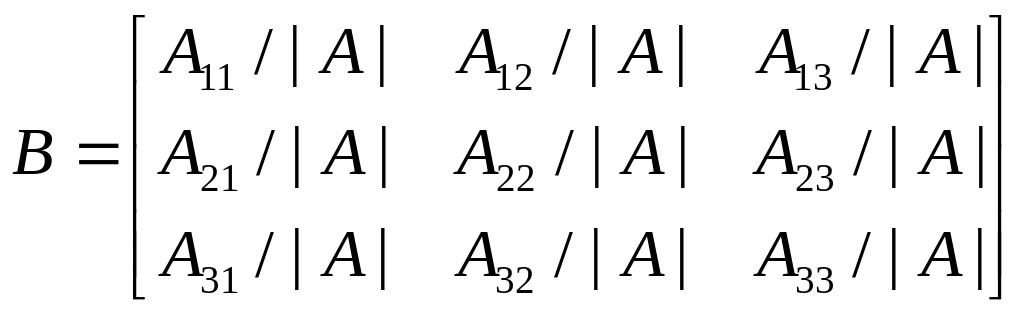
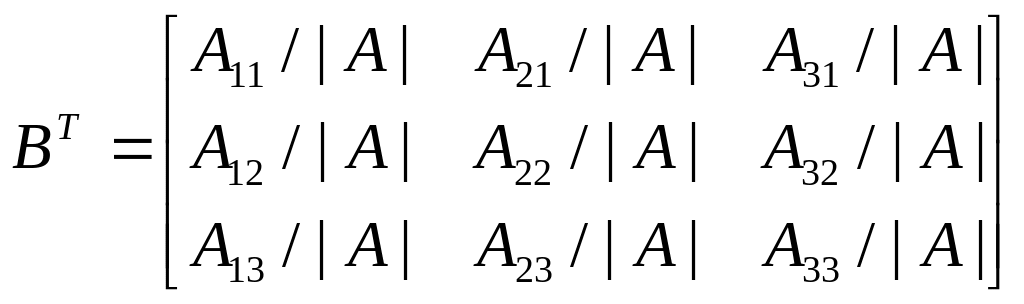
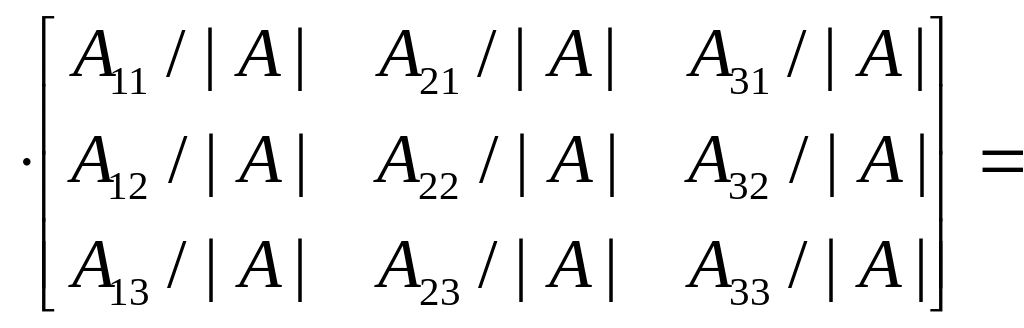
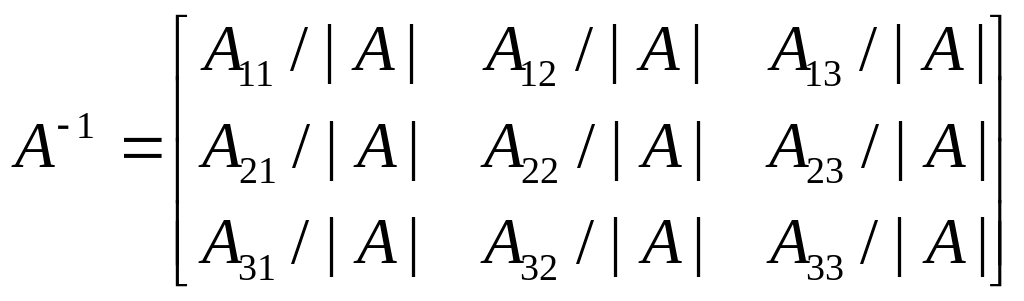