5. Произведение матриц

Произведением матрицы на матрицу называется матрица , каждый элемент которой определяется выражением:

(1.5)

Из определения двух матриц видно, что перемножить можно лишь матрицы, у которых число столбцов первой матрицы сомножителя А равно числу строк второй матрицы сомножителя В.

_{Например, если}

и , то		(1.6)
Из определения умножения матриц следует, что новый элемент равен сумме произведений соответствующих элементов строки и столбца. На рис. 1.1 схематично показано получение элемента, стоящего в первой строке и в первом столбце в произведении матриц.	Рис 1. 2 Схема вычисления элемента

Пример 1.3. Даны две матрицы А и В. Найти и ВА.

Эти примеры показывают, что произведение двух матриц, вообще говоря, не подчиняется переместительному закону: .

Определение 1.1. Матрицы А и В, для которых АВ=ВА, называются коммутативными.

Операция перемножения матриц обладает следующими свойствами:

3. (сочетательный закон);

4. (распределительный закон).

6.Транспонирование матриц

Если строки матрицы А записать в виде столбцов, а столбцы в виде строк, то получим матрицу транспонированную матрицу .

Операция транспонирования обладает следующими свойствами:

1. ;

2. ;

3. ;

4. .

Пример 1.4. Дана матрица А. Найти А^Т.

7.Определители второго порядка и их свойства

Рассмотрим матрицу второго порядка:

(2.1)

Определение 2.1. Определителем (или детерминантом) второго порядка, соответствующим данной матрице, называется число :

(2.2)

Пример 2.1. Вычислить определитель матрицы:

8.Определители высших порядков

Рассмотрим квадратную матрицу размера

.

(2.3)

Определение 2.2. Определителем (или детерминантом) высшего порядка, соответствующим данной квадратной матрице, называют число, получаемое из элементов матрицы А по определенному закону — закону раскрытия определителя.

Это число обозначается

.

(2.4)

Прежде, чем формулировать закон раскрытия определителей высшего порядка, введем понятие минора и алгебраического дополнения.

Определение 2.3. Минором, соответствующим данному элементу определителя n-го порядка, называется определитель (n-1)-го порядка, полученный из данного вычеркиванием строки и столбца, на пересечении которых стоит данный элемент.

Миноры обозначаются буквой М_ij с индексами, соответствующими вычеркнутым номерам строк и столбцов. Так, например, минор М₁₂, соответствующий элементу а₁₂ определителя (2.4), есть определитель

.

(2.5)

Он получается из определителя (2.4) вычеркиванием первой строки и второго столбца.

Определение 2.4. Алгебраическим дополнением элемента определителя называется его минор, взятый со знаком плюс, если сумма номеров строки и столбца, в которых стоит элемент, четна, и со знаком минус, если эта сумма нечетна.

Алгебраическое дополнение элемента а_ij обозначается через A_ij. Здесь i означает номер строки, а j —номер столбца, на пересечении которых находится данный элемент.

Связь между алгебраическим дополнением элемента и его минором выражается следующим равенством:

.

(2.6)

Определение 2.5. Определитель квадратной матрицы равен сумме попарных произведений элементов какой-либо его строки (или столбца) на их алгебраические дополнения:

для любых i	(2.7)
или для любых j.	(2.8)

Определение 2.6. Матрица называется невырожденной, если ее определитель отличен от нуля.

В качестве примера использования формул (2.7) и (2.8) приводятся формулы разложения определителя третьего порядка

(2.9)

по элементам первой строки

(2.10)

и элементам второго столбца

.

(2.11)

Поработаем с формулой (2.10) и раскроем миноры по формуле (3.2):

Итак, раскрыв скобки, получим.

(2.12)

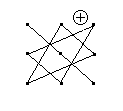
Для запоминания правила вычисления определителя третьего порядка используют модель Саррюса, которая приведена на рис. 2.1. Элементы определителя изображены точками. Перемножают элементы, соединенные линиями, и полученные произведения складывают, снабдив их соответствующими знаками.

Рис 2. 1 Модель Саррюса

Пример 2.2. Вычислить определитель третьего порядка для матрицы:

(2.13)

Воспользуемся формулой (2.7) и раскроем определитель, например, по элементам третьей строки (i=3):

(2.14)

Предварительно вычислим алгебраические дополнения:

Подставим полученные числовые значения алгебраических дополнений в формулу (3.14) и вычислим определитель

(2.15)

Полученное решение можно проверить по формуле (2.12).