40.Сложная функция
Сложная функция – функция от функции. Если z – функция от у, т.е. z(y), а у, в свою очередь, – функция от х, т.е. у(х), то функция f(x) = z(y(x)) называется сложной функцией (или композицией, или суперпозицией функций) от х.
В такой функции х – независимая, а у – промежуточная переменная. При этом сложная функция определена для тех значений независимой переменной, для которых значения промежуточной функции у входят в область определения функции z(y).
Производная дифференцируемой сложной функции равна произведению производной данной функции по промежуточному аргументу на производную промежуточной функции по независимому аргументу:
.
Эта формула легко распространяется на случай, когда у сложной функции имеется два, три и более промежуточных аргументов («цепное правило»): если z = f1(y1), y1 = f2(y2), …, yn-1 = fn(x), то
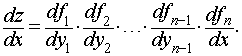
41.Корни алгебраических уравнений
Корень называется алгебраическим, если не требуется, чтобы он извлекался из положительного числа и чтобы сам он был положительный. Таким образом, если под выражением подразумевается алгебраический корень n-й степени, то это значит, что число а может быть и положительное, и отрицательное и сам корень может быть и положительным, и отрицательным. Например, Свойства алгебраических корней. 1) Корень нечётной степени из положительного числа - положительное число, так как отрицательное число, возведённое в степень с нечётным показателем, даёт отрицательное число. Например, 2) Корень нечётной степени из отрицательного числа - отрицательное число, так как положительное число, возведённое в любую степень, даёт положительное число, а не отрицательное. Например, 3) Корень чётной степени из положительного числа имеет два значения с противоположными знаками и с одинаковой абсолютной величиной. Например, 4) Корень чётной степени из отрицательного числа не может равняться никакому, ни положительному, ни отрицательному, числу, так как и то и другое после возведения в степень с чётным показателем даёт положительное число, а не отрицательное.