36.Понятие числовой функции

В математике числовая функция — это функция, области определения и значений которой являются подмножествами числовых множеств — как правило, множества вещественных чисел или множества комплексных чисел

График функции

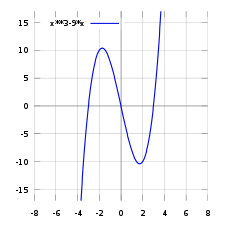
Фрагмент графика функции

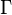• Пусть дано отображение . Тогда его гра́фиком называется множество 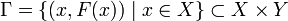     , где обозначает декартово произведение множеств и .

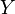  • Графиком непрерывной функции является кривая на двумерной плоскости.

  • Графиком непрерывной функции 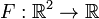является поверхность в трёхмерном пространстве.

Примеры

• Функция Дирихле

  • Возвращает единицу, если аргумент — рациональное число, если же иррациональное, то возвращает ноль.

• Область определения: (вся числовая ось).

• Область значений: .

• Функция sgn(x)

  • Возвращает знак аргумента.

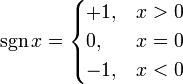
• Область определения: .

• Область значений: .

• 

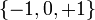  • Область определения: .

  • Область значений: .

• Факториал

  • Возвращает произведение всех натуральных чисел, не больших данного. Кроме того, .

• Область определения: 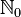(множество натуральных чисел с нулём).

• Область значений:

• Антье (пол)

  • Возвращает целую часть числа.

• Область определения: .

• Область значений: .

Способы задания функции

Словесный	С помощью естественного языка	Игрек равно целая часть от икс.
Аналитический	С помощью формулы и стандартных обозначений
Графический	С помощью графика	Фрагмент графика функции .
Табличный	С помощью таблицы значений	x 0 1 2 3 4 5 6 7 8 9 y 1 1 2 3 5 8 13 21 34 55

Аналитический способ

Обычно функция задаётся с помощью формулы, в которую входят переменные, операции и элементарные функции. Возможно кусочное задание, то есть различное для различных значений аргумента.

Примеры:

• ;

• ;

• ;

• 

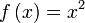Табличный способ

Функцию можно задать, перечислив все её возможные аргументы и значения для них. После этого, если это необходимо, функцию можно доопределить для аргументов, которых нет в таблице, путём интерполяции или экстраполяции. Примерами могут служить программа передач, расписание поездов или таблица значений булевой функции: